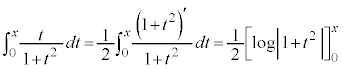���嗝�n���w'24�N�O��[2]
���̊�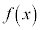 ���l����B
���l����B
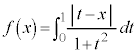 �@(
�@(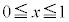 )
)(1) 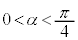 ��������α�ŁA
��������α�ŁA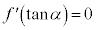 �ƂȂ���̂����߂�B
�ƂȂ���̂����߂�B (2) (1)�ŋ��߂�α�ɑ��A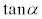 �̒l�����߂�B
�̒l�����߂�B (3) ��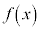 �̋��
�̋��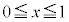 �ɂ�����ő�l�ƍŏ��l�����߂�B�K�v�Ȃ�A
�ɂ�����ő�l�ƍŏ��l�����߂�B�K�v�Ȃ�A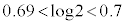 �ł��邱�Ƃ�p���Ă悢�B
�ł��邱�Ƃ�p���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��Βl�t����ϕ�����{���̖��ł����A�{��ł́A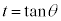 �Ƃ��Ēu���ϕ�������A�������Ȃ��悤�ɒ��ӂ��K�v�ł��B
�Ƃ��Ēu���ϕ�������A�������Ȃ��悤�ɒ��ӂ��K�v�ł��B
��蕶��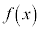 �́A�ϕ���Ԃ�
�́A�ϕ���Ԃ�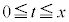 ��
��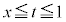 �ɕ����A��Βl���O�����ϕ����܂��B
�ɕ����A��Βl���O�����ϕ����܂��B
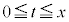 �̂Ƃ��A
�̂Ƃ��A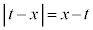
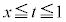 �̂Ƃ��A
�̂Ƃ��A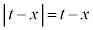
����āA
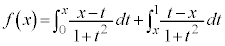 �@����@
�@����@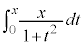 �́A
�́A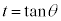 �Ƃ���(�u���ϕ����Q��)�ƁA
�Ƃ���(�u���ϕ����Q��)�ƁA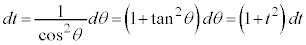 �Ct�F
�Ct�F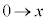 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F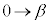 (β��
(�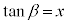 �����p)
�����p)
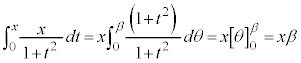 �@����A
�@����A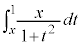 �́A
�́A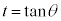 �Ƃ����ƁA
�Ƃ����ƁA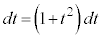 �Ct�F
�Ct�F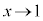 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F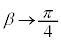 (
(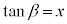 �C
�C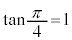 �ł�)
�ł�)
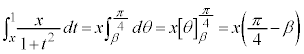 �@����B
�@����B
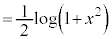 �@����C
�@����C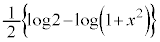 �@����D
�@����D
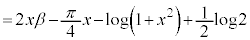 �@����E
�@����E
(1) 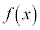 �����������ɂ������āA
�����������ɂ������āA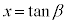 �Ȃ̂ŁAβ��x�̊��ł��邱�Ƃɒ��ӂ��܂��B
�Ȃ̂ŁAβ��x�̊��ł��邱�Ƃɒ��ӂ��܂��B ���A
����āA�E���������ƁA
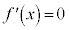 �Ƃ����
�Ƃ����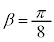 �C�����A
�C�����A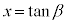 ���
���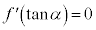 �C
�C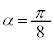 �ƂȂ�α�́A
�ƂȂ�α�́A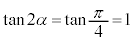 ......[��]
......[��]
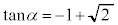 ���A
���A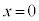 ......[��]�@����F
......[��]�@����F
(3) �E��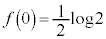 �Ƃ���ƁA
�Ƃ���ƁA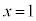
�E��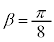 �Ƃ���ƁA���̂Ƃ�
�Ƃ���ƁA���̂Ƃ�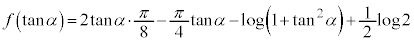 �Ȃ̂ŁA
�Ȃ̂ŁA �����\�́A�ȉ��̂悤�ɂȂ�܂��B���[�̂ǂ���̕����傫���������ɂȂ�܂����A��������Ă݂�ƁA 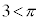 �C
�C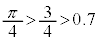 �Ȃ̂ŁA
�Ȃ̂ŁA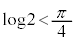 ���A
���A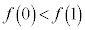 �C�����
�C�����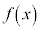
�����\���A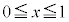 ��
��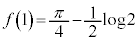 �ɂ�����A�ő�l��
�ɂ�����A�ő�l��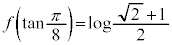 �C�ŏ��l��
�C�ŏ��l��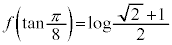 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 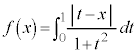 �@(
�@(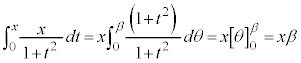 �@����A
�@����A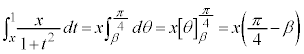 �@����B
�@����B