���嗝�n���w'24�N�O��[6]
2�ȏ�̐����ŁA1�Ƃ��ꎩ�g�ȊO�ɐ��̖������Ȃ�����f���Ƃ����B�ȉ��̖₢�ɓ�����B
(1) 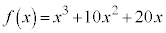 �Ƃ���B
�Ƃ���B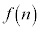 ���f���ƂȂ�悤�Ȑ���n�����ׂċ��߂�B
���f���ƂȂ�悤�Ȑ���n�����ׂċ��߂�B (2) a�Cb�𐮐��̒萔�Ƃ��A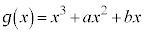 �Ƃ���B
�Ƃ���B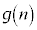 ���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��邱�Ƃ������B
���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@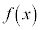 �����������ł��Ă��܂��܂����A2�̐��̐ς��f���ɂȂ�Ƃ��A����2���́A1�Ƒf���A���邢�́A
�����������ł��Ă��܂��܂����A2�̐��̐ς��f���ɂȂ�Ƃ��A����2���́A1�Ƒf���A���邢�́A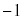 �Ƒf���̕�����ς������̂ɂȂ�܂��B�肪����̂Ȃ�(2)�́A(1)��10��a�C20��b�ɒu��������Ƃǂ��Ȃ邾�낤�A�Ƃ����Ƃ��납��l���Ă����܂��B
�Ƒf���̕�����ς������̂ɂȂ�܂��B�肪����̂Ȃ�(2)�́A(1)��10��a�C20��b�ɒu��������Ƃǂ��Ȃ邾�낤�A�Ƃ����Ƃ��납��l���Ă����܂��B
(1) 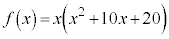 �C
�C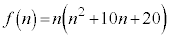 ���f���ł���̂́A
���f���ł���̂́A (i) 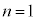 ����
����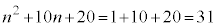 ���f��(���̒l)
���f��(���̒l)
(ii) 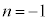 ����
����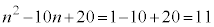 ���f���̕�����ς�����(���̒l)�A(iii) n���f������
���f���̕�����ς�����(���̒l)�A(iii) n���f������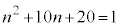 (iv) n���f���̕�����ς������̂���
(iv) n���f���̕�����ς������̂���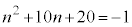
�̂����ꂩ�̏ꍇ�ł��B(i)���A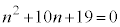 �̂Ƃ�
�̂Ƃ�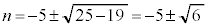 �͑f���ł��B11�͐������Ȃ̂ŁA(ii)�͕s�K�ł��B
�͑f���ł��B11�͐������Ȃ̂ŁA(ii)�͕s�K�ł��B
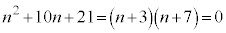 �̉���
�̉���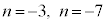 �ł����Đ����ł͂Ȃ��̂�(iii)�͕s�K�ł��B(iv)���A
�ł����Đ����ł͂Ȃ��̂�(iii)�͕s�K�ł��B(iv)���A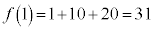 �̉��́A
�̉��́A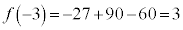 �C����͑f���̕�����ς������̂ł��B
�C����͑f���̕�����ς������̂ł��B
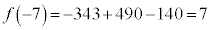 �͑f���ł��B
�͑f���ł��B
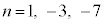 �͑f���ł��B
�͑f���ł��B
����āA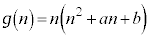 ......[��]
......[��]
(2) 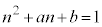 ���f���ƂȂ�̂́A
���f���ƂȂ�̂́A (i) n���f������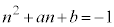
(ii) n���f���̕�����ς������̂���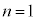
(iii) 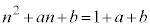 ����
����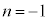 ���f��
���f�� (iv) 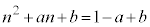 ����
����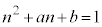 ���f���̕�����ς�������
���f���̕�����ς������� �̂����ꂩ�̏ꍇ�ł��B(i)�̂Ƃ��A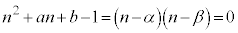 ���A
���A 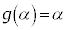 �@����@
�@����@�Ƃ��܂��B2���������̉���2�����Ȃ��̂ŁA�@����n��α�Cβ�ȊO�ɂ͂���܂���B �Eα�Cβ�̂����ꂩ����������f���A�Ⴆ��α�������f���ŁAβ���f���łȂ��Ƃ��́A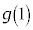 �͑f���ł����A
�͑f���ł����A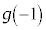 �C
�C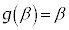 �͑f���̉\��������A
�͑f���̉\��������A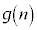 �͑f���ł͂Ȃ��A
�͑f���ł͂Ȃ��A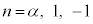 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A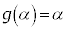 �̍��X3�ł��B
�̍��X3�ł��B �Eα�Cβ���Ƃ��ɑf���ŁA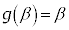 �C
�C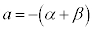 ���Ƃ��ɑf�����Ƃ��܂��B�@�ɂ����āA���ƌW���̊W���A
���Ƃ��ɑf�����Ƃ��܂��B�@�ɂ����āA���ƌW���̊W���A 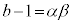 �C
�C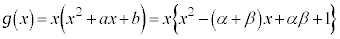
����āA
�����ŁA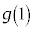 �Ȃ�
�Ȃ�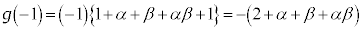 �͑f���̉\��������܂��B
�͑f���̉\��������܂��B α�Cβ�͑f���Ő������Ȃ̂ŁA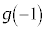 ��
��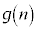 �͑f���ł͂���܂���B����āA���̏ꍇ�A
�͑f���ł͂���܂���B����āA���̏ꍇ�A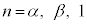 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A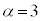 �̍��X3�ł��B
�̍��X3�ł��B
�Ⴆ�A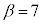 �C
�C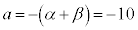 �̂Ƃ��A
�̂Ƃ��A �ŁA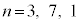 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A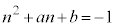 ��3����܂��B
��3����܂��B (ii)�̂Ƃ��A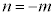 ���A
���A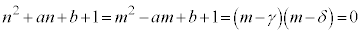 �Ƃ����A
�Ƃ����A 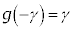 �@����A
�@����A�Ƃ��܂��B�����ŁAγ�Cδ���Ƃ��ɑf���ŁA
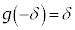 �C
�C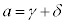
���Ƃ��ɑf�����Ƃ��܂��B�A�ɂ����āA���ƌW���̊W���A
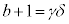 �C
�C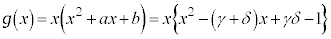
����āA
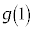 �Ȃ�
�Ȃ�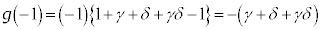 �͑f���̉\��������܂��B
�͑f���̉\��������܂��B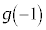 �Ȃ̂�
�Ȃ̂�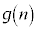 �͑f���ł͂���܂���B����āA���̏ꍇ�A
�͑f���ł͂���܂���B����āA���̏ꍇ�A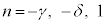 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A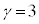 �̍��X3�ł��B
�̍��X3�ł��B
�Ⴆ�A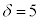 �C
�C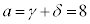 �̂Ƃ��A
�̂Ƃ��A�ŁA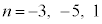 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A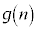 ��3����܂��B
��3����܂��B
�܂��A(i)����n��2�ʂ肠��A(ii)����n��2�ʂ肠��A���킹��4�ʂ��n�����݂��邩���m��܂���Bn�Cm���f�����Ƃ��āA
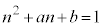 �@����B�@���@
�@����B�@���@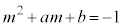 �@����C�@������a�Cb�����݂���Ɖ��肷��ƁA�B�|�C���A
�@����C�@������a�Cb�����݂���Ɖ��肷��ƁA�B�|�C���A n�Cm���Ƃ��ɑf���̏ꍇ�A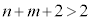 �C
�C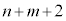 �͐����ł���A
�͐����ł���A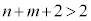 ���A����͕s�����ŁA�B���C����a�Cb�͑��݂��܂���B�܂�A(i)����n��2�ʂ�A(ii)����n��2�ʂ�A�Ƃ������Ƃ͋N����܂���B(iii)�̂Ƃ��A
���A����͕s�����ŁA�B���C����a�Cb�͑��݂��܂���B�܂�A(i)����n��2�ʂ�A(ii)����n��2�ʂ�A�Ƃ������Ƃ͋N����܂���B(iii)�̂Ƃ��A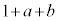 ���f���ł������Ƃ��Ă��A
���f���ł������Ƃ��Ă��A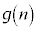 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A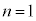 �݂̂ŁA
�݂̂ŁA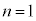 �͑f���ł͂Ȃ�(i)��(ii)�����������A
�͑f���ł͂Ȃ�(i)��(ii)�����������A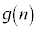 ���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��B(iv)�̂Ƃ����A
���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��B(iv)�̂Ƃ����A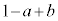 ���f���ł������Ƃ��Ă��A
���f���ł������Ƃ��Ă��A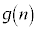 ���f���ƂȂ�n�́A
���f���ƂȂ�n�́A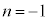 �݂̂ŁA
�݂̂ŁA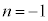 �͑f���ł͂Ȃ�(i)��(ii)�����������A
�͑f���ł͂Ȃ�(i)��(ii)�����������A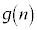 ���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��B
���f���ƂȂ�悤�Ȑ���n�̌���3�ȉ��ł��B
�ȏ���A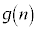 ���f���ƂȂ�n��3�ȉ��ł��B
���f���ƂȂ�n��3�ȉ��ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B