早大理工数学'07年[2]
定数cに対して行列Aを
で定め、直線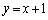
上の動点P
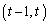をAによって移動した点をQとする。すなわち、
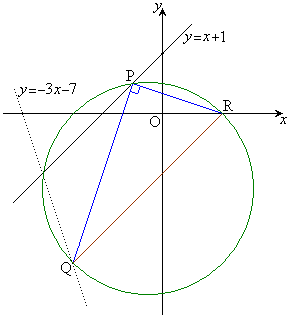
に対応する点をQとする。定点Rとすべてのtの値に対して、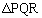
はPを直角の頂点とする直角三角形となるという。以下の問に答えよ。
(1) 定点Rの座標および定数cの値を求めよ。
(2) 三角形PQRの外接円の面積の最小値と、そのときのtの値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 いろいろな解法が考えられますが、直線の傾きを考える(直線の方程式を参照)と場合分けが必要で面倒です。ここでは内積を考えることにします。
問題文が行列を使って書かれていますが、行列の積の計算をするだけで、行列が本質的な問題ではありません。
見易くするために、ベクトル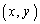
を縦ベクトル
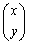で書きます。
(1) Qの位置ベクトルは、
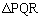がPを直角の頂点とする直角三角形となることから、
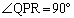，つまり、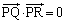
(内積を参照)R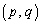
として、 これがすべてのtの値に対して成立するために、
∴ 
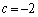......[答] 
，
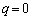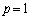
定点Rの座標は、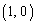
......[答]このとき、
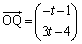です。
(2) 
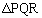がPを直角の頂点とする直角三角形であることから、直角三角形の直径はQR，半径は
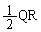，外接円の面積は、
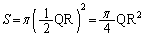になります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
のときに、最大値