���嗝�H���w'08�N[5]
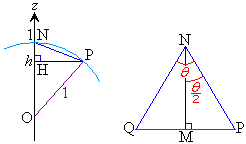
xyz-���W��Ԃɂ����āA���_�𒆐S�Ƃ��锼�a1�̋���S��ɓ_N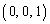 ���Ƃ�B�܂�
���Ƃ�B�܂�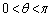 ���݂���θ �ɑ��A����2�̏���
���݂���θ �ɑ��A����2�̏���
(a) 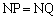
(b) 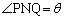
���݂���S��̓��_P�CQ�ɂ��āA����PQ���ʉ߂��Ăł��闧�̐}�`T���l����B�ȉ��̖�ɓ�����B
(1) �_P�Ɠ_Q��z���W�͓��������Ƃ������B
(2) �_P������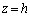 ��ɂ���Ƃ��A����PQ�̒�����θ ��h�ŕ\���B
��ɂ���Ƃ��A����PQ�̒�����θ ��h�ŕ\���B (3) T��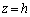 �Ő����Ƃ��̒f�ʂ̊T�`��`���A���̖ʐς�θ ��h�ŕ\���B
�Ő����Ƃ��̒f�ʂ̊T�`��`���A���̖ʐς�θ ��h�ŕ\���B (4) h�̂Ƃ肤��l�͈̔͂ɒ��ӂ��āAT�̑̐�V��θ �ŕ\���Aθ �������Ƃ���V�̍ő�l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �uh�̂Ƃ肤��l�͈̔͂ɒ��ӂ��āv�Ƃ������ӂ��Ȃ��ƁA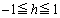 �Ƃ��Ă��܂������ł��B�o��҂͐e�Ȑl�炵���B
�Ƃ��Ă��܂������ł��B�o��҂͐e�Ȑl�炵���B
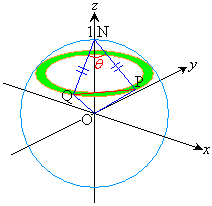 (1) ���_��O�Ƃ��܂��B
(1) ���_��O�Ƃ��܂��B��NPO�Ɓ�NQO�ɂ����āA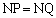 �C
�C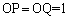 �CON���ʁA���A��NPO�߁�NQO����āAP�CQ����ON (z��)�ɉ��낵�������̑��͈�v���܂��B���̓_��H�CH��z���W��h�Ƃ���ƁAP�CQ��z���W�͂Ƃ���h�œ������Ȃ�܂��B
�CON���ʁA���A��NPO�߁�NQO����āAP�CQ����ON (z��)�ɉ��낵�������̑��͈�v���܂��B���̓_��H�CH��z���W��h�Ƃ���ƁAP�CQ��z���W�͂Ƃ���h�œ������Ȃ�܂��B
���D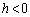 �Ƃ����ꍇ������̂Œ��ӂ��Ă��������B
�Ƃ����ꍇ������̂Œ��ӂ��Ă��������B
 (2) �O�����̒藝���A
(2) �O�����̒藝���A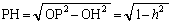 �@����@�@(
�@����@�@(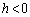 �̏ꍇ������ŗǂ�)
�̏ꍇ������ŗǂ�)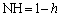 �@(
�@(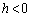 �̏ꍇ������ŗǂ�)
�̏ꍇ������ŗǂ�)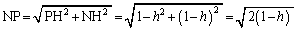
PQ�̒��_�A�����AH����PQ�ɉ��낵�������̑���M�Ƃ��܂��B
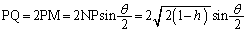 ......[��]�@(
......[��]�@(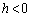 �̏ꍇ������ŗǂ�)
�̏ꍇ������ŗǂ�)
(3) P�CQ���A����S�ƕ���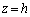 �̌����Ƃ��Ăł���~������Ƃ��A����PQ��̓_R��H�Ƃ̋���HR�́A
�̌����Ƃ��Ăł���~������Ƃ��A����PQ��̓_R��H�Ƃ̋���HR�́A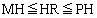 �@����A�@�����܂��B
�@����A�@�����܂��B  �@����B
�@����B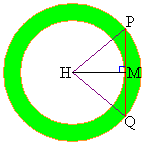 ����Ƈ@���A�s�����A�̍��ӂƉE�ӂ�MH�CPH�́AP�CQ�̈ʒu�Ɉˑ����܂���B
����Ƈ@���A�s�����A�̍��ӂƉE�ӂ�MH�CPH�́AP�CQ�̈ʒu�Ɉˑ����܂���B
������AT�̒f�ʂ̊T�`�́A���a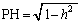 �̉~�Ɣ��a
�̉~�Ɣ��a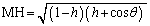 �̉~�ɂ͂��܂ꂽ����(�E�}�ŁA���ΐF�ɒ��F���������A���E�����܂�)�ɂȂ�܂��B
�̉~�ɂ͂��܂ꂽ����(�E�}�ŁA���ΐF�ɒ��F���������A���E�����܂�)�ɂȂ�܂��B
�f�ʂ̖ʐ�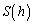 �́A�C��(2)��PM�𗘗p���āA
�́A�C��(2)��PM�𗘗p���āA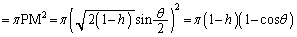 ......[��]�@(
......[��]�@(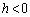 �̏ꍇ������ŗǂ�)
�̏ꍇ������ŗǂ�)
(4) �C�ɂ����āA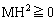 ���A
���A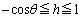 �ł��B
�ł��B  �Ƃ�����(
�Ƃ�����(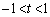 )�A
)�A�����\���(���̑������Q��)�AV�́A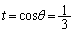 �̂Ƃ��A�ő�l�F
�̂Ƃ��A�ő�l�F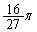 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B