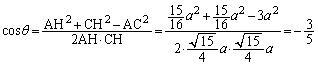���勳�琔�w'10�N[2]
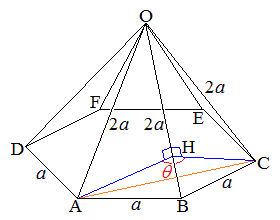
��ʂ����Z�p�`ABCDEF�Œ��_��O�̐��Z�p��O-ABCDEF������B��ʂ̕ӂ̒�����a�C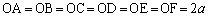 �Ƃ���B2�̖ʁ�OAB�Ɓ�OBC�̂Ȃ��p��θ �Ƃ���Ƃ��A
�Ƃ���B2�̖ʁ�OAB�Ɓ�OBC�̂Ȃ��p��θ �Ƃ���Ƃ��A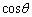 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�}�`���ł����A��ԃx�N�g���ł��A�O�p���p���Ă��ł��܂��B
 �C
�C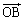 �C
�C ��1���Ɨ��ł��B
��1���Ɨ��ł��B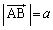 ���A
���A
��  �@����@
�@����@
��OAB�߁�OBC���A���l�ɁA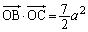 �@����A
�@����A
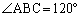 ���A
���A
������A
��  �@����B
�@����B
��OB���H���Ƃ��āA �ƂȂ�悤�ɂ��܂��B���̂Ƃ��A
�ƂȂ�悤�ɂ��܂��B���̂Ƃ��A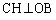 �ł��B
�ł��B
 �Ƃ����ƁA�@��p���āA
�Ƃ����ƁA�@��p���āA
�� 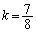 �C
�C
��OAB�Ɓ�OBC�̂Ȃ��pθ �́A���E��BC�ɐ����Ȑ���AH�Ɛ���CH�̂Ȃ��p�ɓ������A
�@��p���āA
 �@����D
�@����D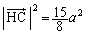 �@����E
�@����E
�@�C�A�C�B��p���āA

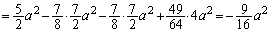 �@����F
�@����F
 ......[��]
......[��]
A����OB�ɐ���H�����낷�ƁA
���l�ɁA
��ABC�ɗ]���藝��K�p���āA
���D�����藝�F ���A
���A �Ƃ��邱�Ƃ��ł��܂��B
�Ƃ��邱�Ƃ��ł��܂��B
��AHC�ɗ]���藝��K�p���āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]