早大教育数学'10年[3]
座標平面上で、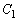 ,
,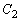 ,
,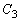 を、それぞれ、中心が
を、それぞれ、中心が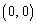 ,
,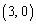 ,
,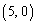 ,半径が2,1,1である円周とする。点Pは点
,半径が2,1,1である円周とする。点Pは点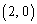 を出発点とし、円周
を出発点とし、円周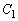 上を反時計回りに等速で
上を反時計回りに等速で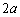 秒で一周する。点Qは点
秒で一周する。点Qは点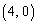 を出発点とし、まず円周
を出発点とし、まず円周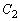 上を反時計回りに等速でa秒で一周し、続いて円周
上を反時計回りに等速でa秒で一周し、続いて円周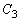 上を時計回りに等速でa秒で一周する。
上を時計回りに等速でa秒で一周する。
点P,Qが同時に出発するとき、線分PQの長さの最大値と最小値を求めよ。ただし、aは正の定数である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 三角関数を含む関数の最大最小の問題です。数学Ⅱの範囲内で解決します。
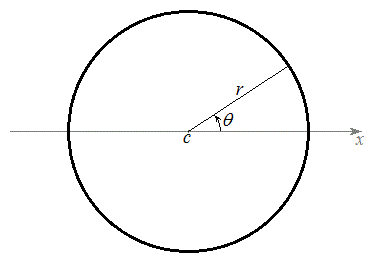 以下では、回転角は各円の中心からx軸方向に進んだ点より出発して反時計回りに測ることにします。円の中心が
以下では、回転角は各円の中心からx軸方向に進んだ点より出発して反時計回りに測ることにします。円の中心が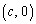 ,半径がr,回転角がθ であれば、動点の座標は
,半径がr,回転角がθ であれば、動点の座標は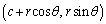 となります。
となります。
また、時刻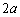 秒でP,Qは初期位置に戻ってくるので、時刻
秒でP,Qは初期位置に戻ってくるので、時刻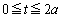 で考えれば十分です。
で考えれば十分です。
時刻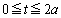 において、点Pは
において、点Pは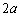 秒で角
秒で角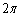 回るので、時刻t での回転角は
回るので、時刻t での回転角は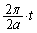 です。円周
です。円周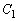 上を回る点Pの座標は
上を回る点Pの座標は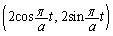 (三角関数を参照)
(三角関数を参照)
時刻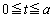 において、点Qはa秒で角π回るので、時刻t での回転角は
において、点Qはa秒で角π回るので、時刻t での回転角は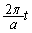 です。円周
です。円周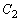 上を回るので、点Qの座標は
上を回るので、点Qの座標は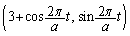
時刻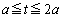 において、点Qはa秒で角π回り、時計回りに、円の中心からx軸負方向に進んだ点より出発するので、時刻tでの回転角は
において、点Qはa秒で角π回り、時計回りに、円の中心からx軸負方向に進んだ点より出発するので、時刻tでの回転角は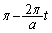 です。円周
です。円周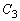 上を回る点Qの座標は
上を回る点Qの座標は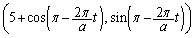
以上を見ると、回転角に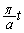 がよく出てくるので、これをθ とおくことにします。つまり、
がよく出てくるので、これをθ とおくことにします。つまり、
このとき、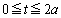 における点Pの座標は
における点Pの座標は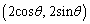
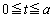 における点Qの座標は
における点Qの座標は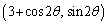
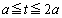 における点Qの座標は、
における点Qの座標は、
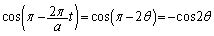 ,
,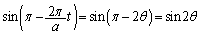
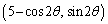
(i) 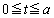 のとき、
のとき、 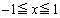 において、
において、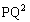 は、
は、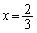 のとき最小値
のとき最小値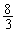 ,
,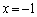 のとき最大値36 ・・・①
のとき最大値36 ・・・①(ii) 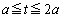 のとき、
のとき、 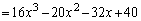 (
(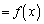 とおきます)
とおきます)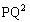 は、
は、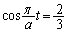 のとき最小値
のとき最小値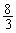 ,
,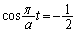 (
(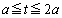 より、
より、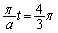 ,つまり、
,つまり、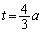 )のとき最大値49
)のとき最大値49
よって、PQの長さの最大値7 (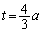 のとき),最小値
のとき),最小値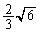 (
(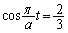 のとき) ......[答]
のとき) ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。