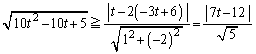���嗝�H���w'10�N[1]
xy���ʏ��2�_A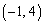 �CB
�CB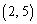 ��ʂ�A����
��ʂ�A����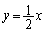 �Ƌ��L�_�����~���l����B�ȉ��̖₢�ɓ�����B
�Ƌ��L�_�����~���l����B�ȉ��̖₢�ɓ�����B
(1) ���̉~�̒��SP�̋O�Ղ����߂�B
(2) ���̉~�̔��ar�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�o�Ă��鐔�l���傫���̂ł����A�Q�ĂȂ��悤�ɒ��ӂ��܂��傤�B
(1) 2�_A�CB��ʂ�~C�̒��S�́A����AB�̐���������ɂ���܂��B
����AB�̌X����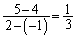 �C����AB�����_��
�C����AB�����_��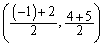 �C�܂�A
�C�܂�A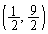 �ł��B������A����AB�̐��������́A�X����
�ł��B������A����AB�̐��������́A�X����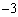 (2�����̕��s�E�������Q��)��
(2�����̕��s�E�������Q��)��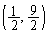 ��ʂ钼���Ȃ̂ŁA
��ʂ钼���Ȃ̂ŁA ������AC�̒��SP�̍��W��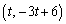 (t�͎���)�Ƃ������Ƃ��ł��܂��BC������
(t�͎���)�Ƃ������Ƃ��ł��܂��BC������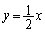 (�����A
(�����A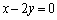 )�Ƌ��L�_��L����̂́AC�̒��SP�ƒ���
)�Ƌ��L�_��L����̂́AC�̒��SP�ƒ���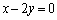 �Ƃ̋������A�~C�̔��a
�Ƃ̋������A�~C�̔��a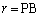 �ȉ��̂Ƃ��ł�(�~�ƒ����̈ʒu�W���Q��)�B
�ȉ��̂Ƃ��ł�(�~�ƒ����̈ʒu�W���Q��)�B 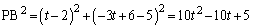 �@����@
�@����@���A
�� 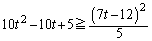
��������ƁA
�� 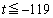 �܂���
�܂��� 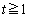 �@����At�͉~�̒��SP��x���W�Ȃ̂ŁA�~�̒��SP���O���́A����
�@����At�͉~�̒��SP��x���W�Ȃ̂ŁA�~�̒��SP���O���́A����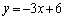 ��
��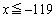 �܂���
�܂���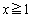 �̕��� ......[��]
�̕��� ......[��]
(2) �A�̂Ƃ��A�@�́A
�ł����āA�����t��2�����ƌ���Ƃ��A�O���t�̎��̈ʒu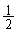 �͇A�Ɋ܂܂�܂��A�A�͈̔͂�t�ł͒[�_
�͇A�Ɋ܂܂�܂��A�A�͈̔͂�t�ł͒[�_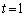 ���ł��߂��A�����Ŕ��ar�͍ŏ��l
���ł��߂��A�����Ŕ��ar�͍ŏ��l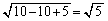 ......[��] ���Ƃ�܂�(2�����̍ő�ŏ����Q��)�B
......[��] ���Ƃ�܂�(2�����̍ő�ŏ����Q��)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B