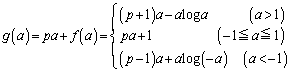早大理工数学'10年[3]
a,bを実数とし、xy平面上の次の2つの関数のグラフについて考える。
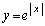 ・・・①
・・・①
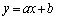 ・・・②
・・・②
(1) ①,②がただ1つの共有点をもつとき、bをaで表し、そのグラフをab平面上に図示せよ。
(2) (1)のグラフを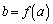 と表す。定数pに対して
と表す。定数pに対して を最大にするaおよびその最大値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (2)は細かくて神経がすり減りますが、難問というわけではなく、丁寧に解答しましょう。
(1) ①: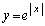 のグラフは、
のグラフは、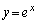 の
の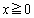 の部分のグラフと、これをy軸に関して対称移動させたグラフを、点P
の部分のグラフと、これをy軸に関して対称移動させたグラフを、点P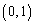 においてつなぎ合わせたグラフです。
においてつなぎ合わせたグラフです。 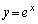 は
は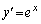 (微分の公式を参照)より点Pにおける接線の傾きは1です。また、
(微分の公式を参照)より点Pにおける接線の傾きは1です。また、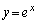 のグラフをy軸に関して対称移動させたグラフの点Pにおける接線の傾きは
のグラフをy軸に関して対称移動させたグラフの点Pにおける接線の傾きは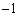 です。
です。
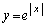 は、
は、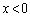 において、また、
において、また、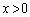 において、下に凸、また
において、下に凸、また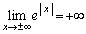 なので、直線②が
なので、直線②が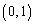 を通るとき、つまり、
を通るとき、つまり、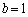 のとき、直線の傾きaが、
のとき、直線の傾きaが、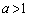 ,あるいは、
,あるいは、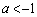 のときには、①と②は、
のときには、①と②は、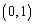 以外にも共有点をもってしまいます(微分法の方程式への応用2を参照)。従って、
以外にも共有点をもってしまいます(微分法の方程式への応用2を参照)。従って、(i) ただ1つの共有点が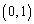 のとき、
のとき、 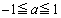 かつ
かつ 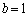
(ii) ただ1つの共有点が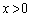 の部分に存在するとき、その共有点をQ
の部分に存在するとき、その共有点をQ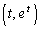 (
(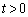 )として、直線②はQにおける①の接線になります。
)として、直線②はQにおける①の接線になります。 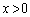 において①は
において①は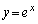 (
(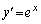 )になるので、接線の傾きaについて、
)になるので、接線の傾きaについて、∴ 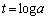 接線が点Qを通ることから、
接線が点Qを通ることから、 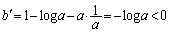 (
(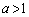 )
)これよりbは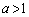 において単調減少(関数の増減を参照)。
において単調減少(関数の増減を参照)。
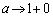 のとき
のとき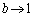 ,
,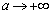 のとき
のとき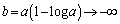
(iii) ただ1つの共有点が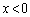 の部分に存在するとき、
の部分に存在するとき、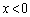 において①は
において①は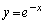 (
(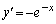 )であって、(ii)と同様に直線②は共有点Q
)であって、(ii)と同様に直線②は共有点Q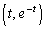 (
(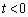 )における接線です。接線の傾きについて、
)における接線です。接線の傾きについて、 ∴ 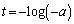 接線が点Qを通ることから、
接線が点Qを通ることから、 ∴ 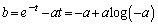
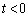 より、
より、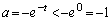
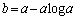 において
において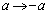 とすると
とすると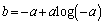 になるので、
になるので、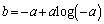 (
(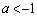 )のグラフは、
)のグラフは、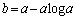 (
(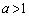 )のグラフをb軸に関して対称移動させたグラフです。
)のグラフをb軸に関して対称移動させたグラフです。 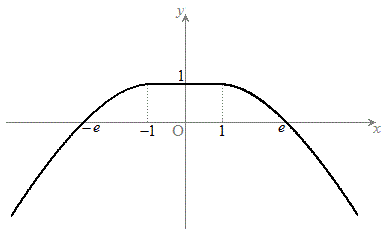 以上より、
以上より、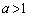 のとき
のとき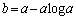 ,
,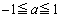 のとき
のとき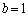 ,
,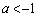 のとき
のとき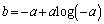 ,求めるグラフは右図実線。
,求めるグラフは右図実線。
(2) 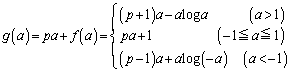
(i) 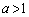 において、
において、 ・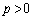 のとき、
のとき、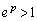
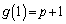 ,
,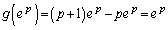
・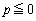 のとき、
のとき、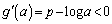
この範囲において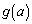 は単調減少で、
は単調減少で、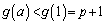
(ii) 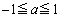 において、
において、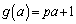
・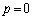 のとき
のとき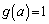 より、この範囲における最大値も1
より、この範囲における最大値も1 (iii) 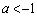 において、
において、 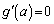 とすると、
とすると、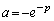
・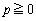 のとき、
のとき、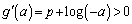
この範囲において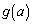 は単調増加で、
は単調増加で、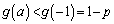
・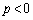 のとき、
のとき、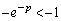
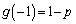 ,
,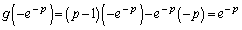
この範囲では最大値は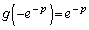
以上より、
・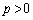 のとき、
のとき、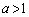 においての最大値
においての最大値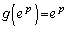 ,
,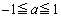 においての最大値
においての最大値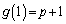 ,
,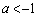 において
において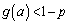
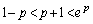 より、最大値は
より、最大値は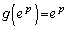
最大値は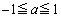 において
において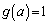
・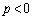 のとき、
のとき、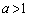 において
において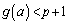 ,
,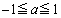 においての最大値
においての最大値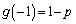 ,
,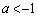 においての最大値
においての最大値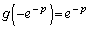
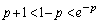 より、最大値は
より、最大値は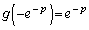
まとめると、
・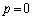 のとき、
のとき、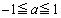 において最大値1
において最大値1
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
早大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。