�k�啨��'09�N�O��[3]
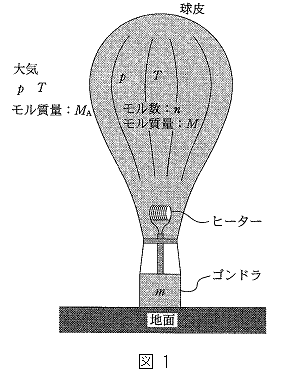 �}1�̂悤�ɁA�f�M�f�ނłł�������ƃS���h��������Ȃ�C�����n�ʂɒu����ĕ��ス���Î~���Ă���B��C(��C)�͉��x
�}1�̂悤�ɁA�f�M�f�ނłł�������ƃS���h��������Ȃ�C�����n�ʂɒu����ĕ��ス���Î~���Ă���B��C(��C)�͉��x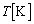 �̗��z�C�̂Ƃ݂Ȃ����Ƃ��ł���B��C�̈��͂͏d�͂̂��ߍ��x���Ⴂ�قǍ������A�����ł͂܂��A���̈��͂̍��x�ˑ��������ċC���̒��S�̍��x�ł̑�C�̈���
�̗��z�C�̂Ƃ݂Ȃ����Ƃ��ł���B��C�̈��͂͏d�͂̂��ߍ��x���Ⴂ�قǍ������A�����ł͂܂��A���̈��͂̍��x�ˑ��������ċC���̒��S�̍��x�ł̑�C�̈���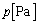 �ŋߎ�����B
�ŋߎ�����B
����A�����ꂽ������ɂ͑�C�Ɠ�������p�Ɖ��xT�����P���q���q���z�C�� �������Ă���A������̋C�̂̓����G�l���M�[
�������Ă���A������̋C�̂̓����G�l���M�[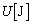 �́A�C�̒萔
�́A�C�̒萔 ��p���āA
��p���āA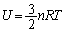 �Ə������Ƃ��ł���B����͍ŏ��\���ɂ��ڂ�Ԃł���A������ɑ������ꂽ�q�[�^�[�ɂ��A������̋C�̂̉��x���㏸�����C�̂̑̐ς�c�������邱�Ƃ��ł���B���̂Ƃ��A������̋C�̂̈��͂Ƒ�C���͏�ɂ荇���Ă���Ƃ���B�ȉ��̕��͂� (1) ���� (10) �ɓK�Ȑ��������A (11) �ɂ͗L������2���̐��l������B
�Ə������Ƃ��ł���B����͍ŏ��\���ɂ��ڂ�Ԃł���A������ɑ������ꂽ�q�[�^�[�ɂ��A������̋C�̂̉��x���㏸�����C�̂̑̐ς�c�������邱�Ƃ��ł���B���̂Ƃ��A������̋C�̂̈��͂Ƒ�C���͏�ɂ荇���Ă���Ƃ���B�ȉ��̕��͂� (1) ���� (10) �ɓK�Ȑ��������A (11) �ɂ͗L������2���̐��l������B
��1�@������̋C�̂̑̐ς́A��ԕ�������� (1) 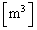 �Ə������Ƃ��ł���B���܃q�[�^�[�ɂ���ĔM��
�Ə������Ƃ��ł���B���܃q�[�^�[�ɂ���ĔM��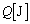 ���������C�̂ɗ^�����Ƃ���A�C�̂̉��x�Ƒ̐ς����ꂼ��
���������C�̂ɗ^�����Ƃ���A�C�̂̉��x�Ƒ̐ς����ꂼ��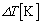 �����
�����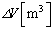 �����ω������B���̉ߒ��ŋ�����̋C�̂��O���ɂ����d���� (2)
�����ω������B���̉ߒ��ŋ�����̋C�̂��O���ɂ����d���� (2) 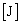 �ł���A���̓����G�l���M�[�̕ω��� (3)
�ł���A���̓����G�l���M�[�̕ω��� (3) 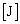 �ƂȂ�B���������āA�M�͊w���@�����AQ��
�ƂȂ�B���������āA�M�͊w���@�����AQ��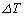 �����
�����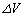 ��p����
��p����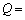 (4)
(4) 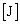 �ƕ\����B���̎��Ə�ԕ������ɂ��A������̋C�̂̒舳������M
�ƕ\����B���̎��Ə�ԕ������ɂ��A������̋C�̂̒舳������M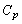
 (���͈��̏�����
(���͈��̏����� �̋C�̂�P�ʉ��x�㏸������̂ɕK�v�ȔM��)��R��p����
�̋C�̂�P�ʉ��x�㏸������̂ɕK�v�ȔM��)��R��p���� (5)
(5)  �Ə������Ƃ��ł���B
�Ə������Ƃ��ł���B
�S���h���̎��ʂ�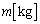 �C������̋C�̂Ƌ�C�̃�������(
�C������̋C�̂Ƌ�C�̃�������( ������̎���)�����ꂼ��
������̎���)�����ꂼ��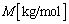 �����
�����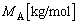 �Ƃ��A�d�͉����x�̑傫����
�Ƃ��A�d�͉����x�̑傫����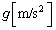 �Ƃ���B�܂��A�C���̎��ʂ͋�����̋C�̂ƃS���h���̎��ʂ݂̂��l�����A�ق��͂��ׂĖ�������B�C���̑̐ς͋�����̋C�̂̑̐ς݂̂��l�����A�ق��͂��ׂĖ�������B
�Ƃ���B�܂��A�C���̎��ʂ͋�����̋C�̂ƃS���h���̎��ʂ݂̂��l�����A�ق��͂��ׂĖ�������B�C���̑̐ς͋�����̋C�̂̑̐ς݂̂��l�����A�ق��͂��ׂĖ�������B
��2�@�C���ɓ����d�͂̑傫���� (6) 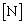 �ł���B����A�C����}1�̏�Ԃ��牷�߂đ̐ς�
�ł���B����A�C����}1�̏�Ԃ��牷�߂đ̐ς�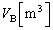 �ɂȂ����Ƃ���ƁA���̑̐�
�ɂȂ����Ƃ���ƁA���̑̐�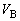 ���߂Ă�����C�̃������́AT��p��p���� (7)
���߂Ă�����C�̃������́AT��p��p���� (7)  �ƕ\����B�d�͂̂��ߑ�C�̈��͉͂����قǍ����B���̂��Ƃ��畂�͂�������B���͂̑傫���̓A���L���f�X�̌������琳�m�ɋ��߂��A�C���ɓ������͂̑傫���� (8)
�ƕ\����B�d�͂̂��ߑ�C�̈��͉͂����قǍ����B���̂��Ƃ��畂�͂�������B���͂̑傫���̓A���L���f�X�̌������琳�m�ɋ��߂��A�C���ɓ������͂̑傫���� (8) 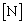 �ƂȂ�B�ȏ���A�C���コ����ɂ͂��̑̐�
�ƂȂ�B�ȏ���A�C���コ����ɂ͂��̑̐�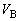 �� (9)
�� (9) 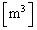 ���傫������K�v������A�C���� (10)
���傫������K�v������A�C���� (10) 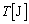 ��葽���M�ʂ�^���Ȃ���Ȃ�Ȃ��B
��葽���M�ʂ�^���Ȃ���Ȃ�Ȃ��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�M�C���コ���邽�߂ɁA�C�̂̉��x���ǂ�قǍ�������悢���A���l�����{���ł��B
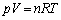 �@����@
�@����@�� 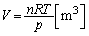
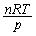 ......[��]
......[��](2) �̐���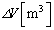 �ω�����Ƃ��A�C�̂��O���ɂ����d���́A
�ω�����Ƃ��A�C�̂��O���ɂ����d���́A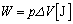
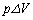 ......[��]
......[��]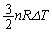 ......[��]
......[��]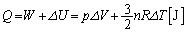 �@����A
�@����A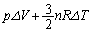 ......[��]
......[��](5) �q�[�^�[���M��^����Ƃ��A������̋C�̂�(��C���Ə�ɂ荇���Ă���̂�)�舳�ω����A�ω����������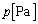 �ŁA��ԕ������F
�ŁA��ԕ������F 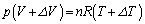 �@����B
�@����B�B�|�@���A
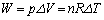 �@����C
�@����C�A���A
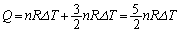 �@����D
�@����D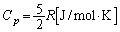
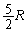 ......[��]
......[��]
��2(6) ������̋C�̂�������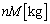 �C�S���h��������
�C�S���h��������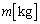 �ƍ��킹�āA
�ƍ��킹�āA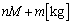
����ɓ����d���̑傫���́A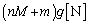
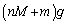 ......[��]
......[��](7) �̐�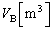 ���߂��C�̃�������
���߂��C�̃�������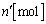 �Ƃ��āA��ԕ������F
�Ƃ��āA��ԕ������F �� 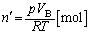
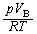 ......[��]
......[��](8) �A���L���f�X�̌������A�C���ɓ��������̑傫���́A������ɋ�C������Ƃ����Ƃ��̋�C�ɓ����d���̑傫���ɓ�����(�����̌������d���Ƌt����)�A 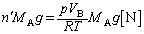
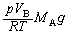 ......[��]
......[��](9) �C���ɓ��������̑傫�����C���ɓ����d���̑傫��������ƋC�������サ�܂��B
�� 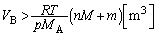 (
(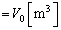 �Ƃ����܂�)
�Ƃ����܂�) 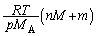 ......[��]
......[��](10) ������J�n����܂Ńq�[�^�[�ʼn��߂�Ԃ��̐ϕω��́A
�C�C�D���A�C���ɗ^����ׂ��M���́A
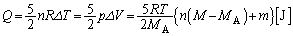 �@����E
�@����E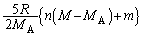 ......[��]
......[��](11) �C�������シ��Ƃ��̃w���E���K�X�����x��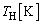 �Ƃ���ƁA������J�n����܂ł����x�ω��́A
�Ƃ���ƁA������J�n����܂ł����x�ω��́A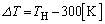
�E���ɐ��l������āA
�� 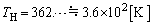
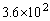 ......[��]
......[��]���D��蕶�ɗ^�����Ă��鐔�l�̗L���������o���o���ł����A���������ꍇ�ɂ́A�ł����Ȃ��L�������Ō���悤�ɂ��܂��B�{��ł́AM��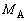 ��2�����ł����Ȃ��̂ŁA���L������2���œ����܂��B
��2�����ł����Ȃ��̂ŁA���L������2���œ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B