北大物理'10年後期[2]
次の文章の (1) から (8) に適切な数式を入れよ。また、 (i) と (ii) には選択肢の欄から適切なものを選び、記号で答えよ。
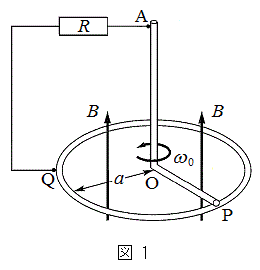問1 図1のように、磁束密度
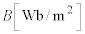の一様な鉛直上向きの磁場中に半径
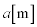の導体円環を水平に置き、その上にL字型の導体棒AOPを、Oが円環の中心にくるように乗せる。AOPは円環とPで接触しながら、AOのまわりで滑らかに回転できる。この導体棒と導体円環の間に抵抗
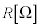の抵抗器を取り付けることにより、閉じた回路AOPQAをつくる。導体の太さ、抵抗および回路の自己インダクタンスは無視できるものとする。
導体棒を一定の角速度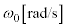
で図1の向きに回転させたところ、回路に電流が流れた。この回転によって導体棒OP中の自由電子は (i) に磁場からローレンツ力を受け、このことにより誘導起電力が発生する。時間
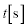の間にOPが円環内を通過する面積は (1) 
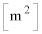と表されるので、OP間に生ずる誘導起電力の大きさは (2) 
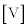となる。また、この時間tの間に抵抗器で発生するジュール熱は (3) 
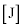である。
(i) の選択肢
(ア) OからPの向き (イ) PからOの向き
(ウ) Pの進む向き (エ) Pの進む向きと逆向き
(オ) 鉛直上向き (カ) 鉛直下向き |
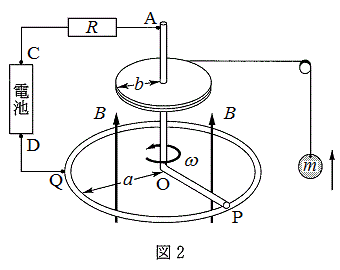問2 次に、図2のように、AOに半径
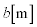の糸巻きを取り付け、糸の先端に質量
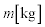のおもりをつける。さらに抵抗器と直列に、内部抵抗を無視できる起電力
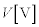の電池を接続する。重力加速度の大きさを
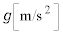とする。
電池を (ii) となるように接続したとき、導体棒と糸巻きが図2の向きに回転しておもりが巻き上がり、その回転はほどなく一定の角速度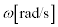
になった。このとき回路を流れる電流の大きさを
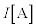とすれば、この電流による抵抗器での電圧降下と導体棒OPで発生する誘導起電力の和が
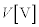であることから、
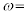(4) 
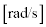と表される。また、このとき導体棒OPが磁場から受ける力の大きさは
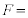(5) 
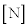である。
角速度が一定のときには、回転軸AOのまわりの力のモーメントがつりあっている。力FはOPに一様に作用しているので、モーメントを考える上では力の作用点はOPの中点と考えてよい。この力のモーメントとおもりによる大きさ (6)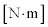 
の力のモーメントとのつりあいから、
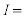(7) 
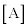の電流が流れていることがわかる。
時間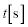
の間におもりが受ける仕事は、位置エネルギーの変化から、ω を用いて (8) 
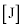と求められるが、この仕事と抵抗器で発生するジュール熱の和は、電池のする仕事
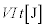に等しい。
(ii) の選択肢
| (ア) Cが正極、Dが負極 (イ) Dが正極、Cが負極 |
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円内を時計の針のように回る導体棒に発生する誘導起電力を扱う問題です。
問1(i) 導体棒OP中の自由電子(負電荷)は上から見て、反時計回りに回転するので、実質的に時計回りの方向に電流が流れる効果があります。これを左手中指の向きとします。磁場の向きを左手人差し指の向きとします。フレミング左手の法則より、自由電子は左手親指の向き、つまり、P→Oの向きに磁場からローレンツ力を受けます。(イ) ......[答] (1) 時間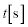
の間のOPの回転角は
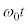です。この間にOPが円環内を通過する面積Sは、 
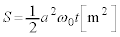(一般角を参照)
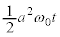......[答](2) 時間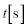
の間にOPが円環内を通過する部分を貫く磁束Φは、 
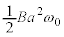......[答](3) 抵抗器に流れる電流Iは、
時間tの間に抵抗器で発生するジュール熱は、
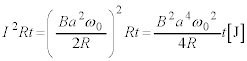(電力を参照)
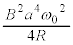......[答]
問2(ii) 図2の矢印の向きにOPを回転させるために、OPは、上から見て反時計回りの力を受けるはずです。この力の向きが、左手親指の方向、磁場の向きが左手人差し指の向き、すると、フレミング左の法則により、左手中指はP→Oの方向を向き、この方向に電流が流れるはずです。このように電流を流すとき、Dが正極、Cが負極となります。(イ) ......[答] (4) 抵抗器での電圧降下は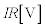
です。OPで発生する誘導起電力は、問1(2)と同様に、
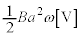，よって、 ∴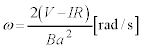 
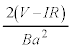......[答](5) 導体棒OPが磁場から受ける力の大きさは、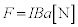
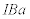......[答](6) おもりによるモーメントは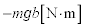
，モーメントの大きさは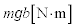
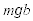......[答]∴ 
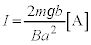
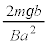......[答](8) おもりが巻き上がる速さは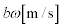
，時間
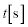の間に、おもりが上昇する距離は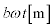
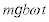......[答]この仕事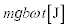
と抵抗器で発生するジュール熱
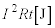の和は、 となり、電池がする仕事に一致します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(∵ (4))
に等しくなります。