慶大理工物理'10年[2]
以下の文章中の に適切な数式または数値を記入しなさい。ただし、解答に使える物理量は、
に適切な数式または数値を記入しなさい。ただし、解答に使える物理量は、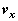 と
と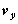 および、V,m,
および、V,m,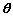 ,
,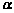 ,
,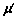 だけとする。
だけとする。
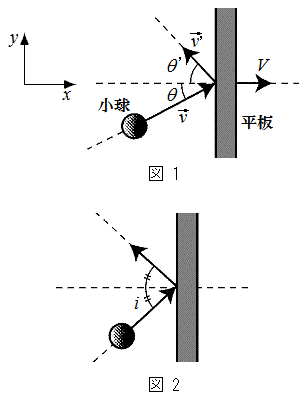 (1) 小球が図1のように、運動するなめらかな平板と弾性衝突をして進行方向を変える。x,y軸を図1の方向にとり、小球はx-y平面内で運動するものとする。小球が平板に衝突する前後の速度は、静止した観測者から見てそれぞれ
(1) 小球が図1のように、運動するなめらかな平板と弾性衝突をして進行方向を変える。x,y軸を図1の方向にとり、小球はx-y平面内で運動するものとする。小球が平板に衝突する前後の速度は、静止した観測者から見てそれぞれ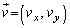 ,
,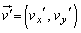 であり、
であり、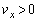 ,
,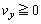 とする。平板はx軸に垂直で十分に広く、その速度のx成分は一定値Vであり、y成分は0で、これらは小球との衝突により変化しないとする。ただし、Vは正負いずれの値もとるが、小球と平板が衝突するように
とする。平板はx軸に垂直で十分に広く、その速度のx成分は一定値Vであり、y成分は0で、これらは小球との衝突により変化しないとする。ただし、Vは正負いずれの値もとるが、小球と平板が衝突するように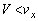 を満たす。図1のように小球の入射角をθ,反射角を
を満たす。図1のように小球の入射角をθ,反射角を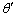 とすると、
とすると、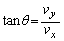 および
および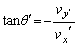 の関係がある。なお、重力や小球の回転運動は考えなくてよい。
の関係がある。なお、重力や小球の回転運動は考えなくてよい。平板とともに運動する観測者から見ると、小球の速度のx成分は、衝突前は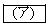 ,衝突後は
,衝突後は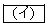 である。これを静止した観測者から見ると、衝突後の小球の速度のx成分は
である。これを静止した観測者から見ると、衝突後の小球の速度のx成分は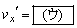 である。
である。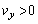 の場合は、平板とともに運動する観測者から見ると、小球と平板の衝突は図2のように見える。このときの入射角をiとすると、
の場合は、平板とともに運動する観測者から見ると、小球と平板の衝突は図2のように見える。このときの入射角をiとすると、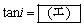 である。また、平板とともに運動する観測者から見ると、入射角と反射角が等しいこともわかる。一方、静止した観測者から見た反射角
である。また、平板とともに運動する観測者から見ると、入射角と反射角が等しいこともわかる。一方、静止した観測者から見た反射角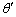 は、
は、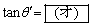 を満たす。このことから、
を満たす。このことから、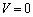 のときだけ
のときだけ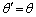 となり、
となり、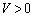 では
では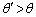 ,
,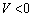 では
では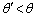 となることがわかる。また、(オ)より、
となることがわかる。また、(オ)より、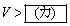 ならば
ならば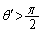 となり、小球は衝突後もx方向に進み続ける(
となり、小球は衝突後もx方向に進み続ける(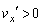 )。このように入射角がθ のとき、
)。このように入射角がθ のとき、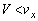 の範囲でVを変えれば、反射角
の範囲でVを変えれば、反射角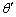 を
を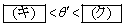 の領域で変化させることができる。
の領域で変化させることができる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 考えにくい相対運動の問題です。以下では細かく丁寧に検討していますが、空所補充問題でもあり、本番では、正負に注意すれば、もっと感覚的に解答してよいと思います。
(1)(ア) 衝突前、平板、小球のx方向の速度成分はそれぞれV,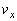 です。平板とともに運動する観測者から見ると、小球の速度のx成分は、
です。平板とともに運動する観測者から見ると、小球の速度のx成分は、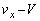 ......[答] (相対速度を参照)
......[答] (相対速度を参照) よって、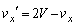
(イ) 衝突後、平板、小球のx方向の速度成分はそれぞれV,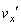 です。平板とともに運動する観測者から見ると、小球の速度のx成分は、
です。平板とともに運動する観測者から見ると、小球の速度のx成分は、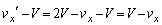
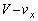 ......[答]
......[答](ウ) 静止した観測者から見ると、衝突後の小球の速度のx成分は、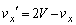 ......[答]
......[答] (エ) 平板とともに運動する観測者から見て、図2の小球の速度のx成分は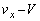 ,y成分は
,y成分は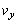 ,よって、
,よって、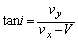
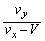 ......[答]
......[答]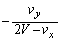 ......[答]
......[答]∴ 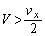
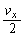 ......[答]
......[答]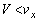 の範囲でVを変えると、
の範囲でVを変えると、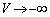 とするとき、
とするとき、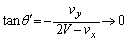
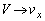 とするとき、
とするとき、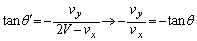
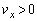 ,
,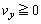 なので、
なので、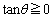 ,
,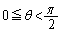
また、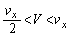 では
では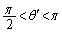 なので、
なので、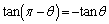 (三角関数を参照)に注意して、
(三角関数を参照)に注意して、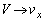 のとき、
のとき、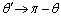
よって、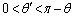
(キ) 0 ......[答]
(ク) 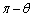 ......[答]
......[答]
(2)(ケ) 小球が平板からはね返らなかったので、衝突直後の小球の速度のx成分は時刻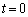 での平板の速度Vに一致します。(ウ)の結果で、
での平板の速度Vに一致します。(ウ)の結果で、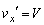 とすると、
とすると、 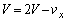 ,∴
,∴ 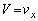
よって、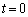 での平板の速度Vは、
での平板の速度Vは、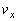 ......[答]
......[答] (コ) 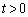 になっても小球は平板から離れず、平板(加速度
になっても小球は平板から離れず、平板(加速度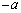 で運動する)とともに運動する観測者から見ると、x軸正方向に慣性力
で運動する)とともに運動する観測者から見ると、x軸正方向に慣性力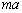 が働きます。また、小球は平板と接触しているので、平板からx軸負方向の垂直抗力N (
が働きます。また、小球は平板と接触しているので、平板からx軸負方向の垂直抗力N (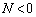 )を受けます。平板とともに運動する観測者から見て、力のつり合いより、
)を受けます。平板とともに運動する観測者から見て、力のつり合いより、 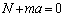 ∴
∴ 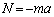
時刻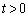 に小球が平板から受ける力のx成分は、
に小球が平板から受ける力のx成分は、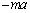 ......[答]
......[答] (サ) 静止した観測者から見て、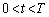 の間、小球はx方向に加速度
の間、小球はx方向に加速度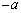 で等加速度運動をします。時刻tにおける小球の速度のx成分vは、
で等加速度運動をします。時刻tにおける小球の速度のx成分vは、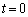 において
において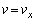 より、
より、 時刻Tにおける小球の速度のx成分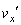 は、
は、 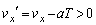 となるためには、
となるためには、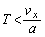
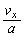 ......[答]
......[答](シ) 平板とともに運動する観測者から見て、平板と接触を続ける小球が平板からy方向に受ける力は、動摩擦力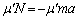 (摩擦力を参照)で、
(摩擦力を参照)で、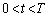 の間、小球はy方向に加速度
の間、小球はy方向に加速度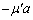 で等加速度運動します。
で等加速度運動します。 時刻tにおける小球の速度のy成分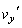 は、
は、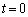 において
において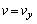 より、
より、 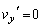 となる時刻は、
となる時刻は、小球はy方向に一旦停止すれば動摩擦が静止摩擦に変わり、そのまま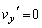 となります。
となります。
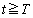 において
において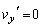 となるために、
となるために、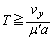
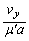 ......[答]
......[答](ス) 「このようなTが存在するための条件」とは、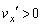 ,
,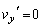 となるようなTが存在するための条件、ということであって、(サ)(シ)の条件をともに満たすTが存在するための条件で、
となるようなTが存在するための条件、ということであって、(サ)(シ)の条件をともに満たすTが存在するための条件で、 であれば、条件を満たすTが存在します。よって、
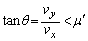
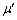 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 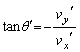 で与えると、
で与えると、