���啨��'04�N�O��[2]
���̕���ǂ�ŁA�@�@�ɓK�����������ꂼ��̉��ɋL������B�Ȃ��A�����ɑ}�����ꂽ��1�ɂ��ẮA���ɃO���t��`���B
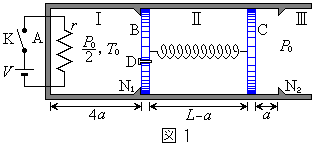 �@�}1�̂悤�ɁA��[����A�ŕ���ꂽ�A�f�ʐ�S�̃V�����_�[������A���C�Ȃ��œ������Ƃ��ł���s�X�g��B�CC�ɂ����3�̋�ԗ̈�T�C�U�C�V�ɕ������Ă���B�̈�T�ɂ͓d�C��Rr�̃j�N�������łł����q�[�^�[������A������R���ł���N�d��V�̓d�r�ƃX�C�b�`K�łł����O���̉�H�ɓ����łȂ���Ă���B�s�X�g��B�ɂ͂����ׂ��ʋC�����J�����Ă��邪�A�ŏ��͕�D�ɂ���ĕ����Ă���B�s�X�g��B�CC�́A�t�b�N�̖@���ɏ]�����R�̒�����L�̂˂Ō���Ă���B�V�����_�[���ɂ́A��A���狗��
�@�}1�̂悤�ɁA��[����A�ŕ���ꂽ�A�f�ʐ�S�̃V�����_�[������A���C�Ȃ��œ������Ƃ��ł���s�X�g��B�CC�ɂ����3�̋�ԗ̈�T�C�U�C�V�ɕ������Ă���B�̈�T�ɂ͓d�C��Rr�̃j�N�������łł����q�[�^�[������A������R���ł���N�d��V�̓d�r�ƃX�C�b�`K�łł����O���̉�H�ɓ����łȂ���Ă���B�s�X�g��B�ɂ͂����ׂ��ʋC�����J�����Ă��邪�A�ŏ��͕�D�ɂ���ĕ����Ă���B�s�X�g��B�CC�́A�t�b�N�̖@���ɏ]�����R�̒�����L�̂˂Ō���Ă���B�V�����_�[���ɂ́A��A���狗��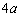 �̈ʒu�ɃX�g�b�p�[
�̈ʒu�ɃX�g�b�p�[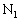 ���A�����
���A�����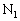 ����˂̎��R��L�ƃs�X�g��B�CC�̌��������킹�������̈ʒu�ɃX�g�b�p�[
����˂̎��R��L�ƃs�X�g��B�CC�̌��������킹�������̈ʒu�ɃX�g�b�p�[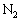 ���݂����A�s�X�g�����~�ł���悤�ɂȂ��Ă���B�������AL��
���݂����A�s�X�g�����~�ł���悤�ɂȂ��Ă���B�������AL��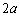 ���傫���B�܂��A�V�����_�[�ƃs�X�g���͂Ƃ��ɒf�M�ނłł��Ă���A�X�g�b�p�[�A�ˁA�فA�ʋC���A�q�[�^�[����ѓ����̑̐ς́A������������ł�����̂Ƃ���B�Ȃ��A��C����
���傫���B�܂��A�V�����_�[�ƃs�X�g���͂Ƃ��ɒf�M�ނłł��Ă���A�X�g�b�p�[�A�ˁA�فA�ʋC���A�q�[�^�[����ѓ����̑̐ς́A������������ł�����̂Ƃ���B�Ȃ��A��C����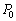 �Ƃ���B
�Ƃ���B
�ŏ��́A�̈�U�͐^��ŁA�̈�T�ɂ͒P���q���q���z�C�̂�������A���̈��͂Ɖ��x�����ꂼ��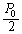 �C
�C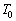 �ł������B�܂��A�̈�V�͏�ɑ�C��
�ł������B�܂��A�̈�V�͏�ɑ�C��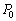 �̊O�C�ƒʂ��Ă���B�}1�Ɏ������悤�ɁA���̏�ԂŃs�X�g��B�̓X�g�b�p�[
�̊O�C�ƒʂ��Ă���B�}1�Ɏ������悤�ɁA���̏�ԂŃs�X�g��B�̓X�g�b�p�[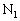 �ɐڐG���Ē�~���A�s�X�g��C�̓X�g�b�p�[
�ɐڐG���Ē�~���A�s�X�g��C�̓X�g�b�p�[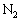 ���狗��a�̈ʒu�Œ�~���Ă����B���̂��Ƃ���A�˒萔���@�C�@�ł��邱�Ƃ�������B���̌�A�ȉ��̂悤�ɉߒ�(1)����(4)�̏��ɃV�����_�[�̏�Ԃ�ω��������B
���狗��a�̈ʒu�Œ�~���Ă����B���̂��Ƃ���A�˒萔���@�C�@�ł��邱�Ƃ�������B���̌�A�ȉ��̂悤�ɉߒ�(1)����(4)�̏��ɃV�����_�[�̏�Ԃ�ω��������B
(1) �X�C�b�`K����ĉ�H�ɓd���𗬂��ƁA�̈�T�̋C�̂̉��x�͂������Ə㏸���A���鎞���Ƀs�X�g��B���X�g�b�p�[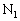 �𗣂�n�߂��B���̂Ƃ��̗̈�T�̋C�̂̉��x���@���@�ł������B�d�r�ɂ�苟�����ꂽ�G�l���M�[�����ׂċC�̂ɋz�����ꂽ�Ƃ���A���̎����̓X�C�b�`K����Ă��玞���@�n�@�̌�ł���B
�𗣂�n�߂��B���̂Ƃ��̗̈�T�̋C�̂̉��x���@���@�ł������B�d�r�ɂ�苟�����ꂽ�G�l���M�[�����ׂċC�̂ɋz�����ꂽ�Ƃ���A���̎����̓X�C�b�`K����Ă��玞���@�n�@�̌�ł���B (2) ���̌�A�s�X�g��B�͂������ƈړ����A�̈�T�̋C�̂̉��x���@�j�@�ɂȂ�ƁA�s�X�g��C���X�g�b�p�[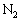 �ɐڐG����~�����B���̉ߒ��ŗ̈�T�̋C�̂��z�������M�ʂ��@�z�@�ł���B
�ɐڐG����~�����B���̉ߒ��ŗ̈�T�̋C�̂��z�������M�ʂ��@�z�@�ł���B (3) ����Ƀs�X�g��B�͂������ƈړ����A�s�X�g��B�CC�Ԃ̋������k�܂��Ă������B�˂̒�����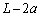 �ɒB�������_�ŃX�C�b�`K���J�����B���̂Ƃ��̈�T�̋C�̂̉��x���@�w�@�ł���A�ߒ�(3)�ŗ̈�T�̋C�̂��z�������M�ʂ��@�g�@�ł���B
�ɒB�������_�ŃX�C�b�`K���J�����B���̂Ƃ��̈�T�̋C�̂̉��x���@�w�@�ł���A�ߒ�(3)�ŗ̈�T�̋C�̂��z�������M�ʂ��@�g�@�ł���B 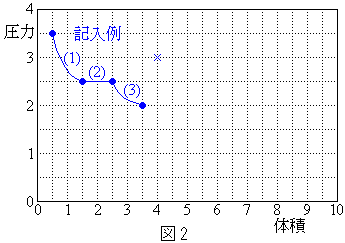 ��1 (1)����(3)�܂ł̉ߒ��ɂ�����̈�T�̋C�̂̏�ԕω��̗l�q���A�}2�̂悤�ɑ̐ς������ɁA���͂��c���ɂƂ�A���ɃO���t�Ŏ����B�O���t�p���̉����Əc���̖ڐ���̐��l�́A���ꂼ���
��1 (1)����(3)�܂ł̉ߒ��ɂ�����̈�T�̋C�̂̏�ԕω��̗l�q���A�}2�̂悤�ɑ̐ς������ɁA���͂��c���ɂƂ�A���ɃO���t�Ŏ����B�O���t�p���̉����Əc���̖ڐ���̐��l�́A���ꂼ���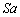 ��
��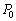 ��1�Ƃ��ĕ\���Ă���B�Ⴆ�ΐ}���́~��̓_�́A�̐ς�
��1�Ƃ��ĕ\���Ă���B�Ⴆ�ΐ}���́~��̓_�́A�̐ς�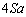 �C���͂�
�C���͂�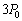 �̏�ԂɑΉ�����B�O���t�͊T�����������̂ł悢���A�}���̋L����ɂȂ���āA�e�ߒ��̎n�_�ƏI�_�ɍ��ہE���A����ɓK���Ȉʒu��(1)�C(2)�C(3)�̔ԍ���t���A�O���t�̂��ꂼ��̕������ǂ̉ߒ���\������������悤�ɂ��邱�ƁB
�̏�ԂɑΉ�����B�O���t�͊T�����������̂ł悢���A�}���̋L����ɂȂ���āA�e�ߒ��̎n�_�ƏI�_�ɍ��ہE���A����ɓK���Ȉʒu��(1)�C(2)�C(3)�̔ԍ���t���A�O���t�̂��ꂼ��̕������ǂ̉ߒ���\������������悤�ɂ��邱�ƁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�u�˂��s�X�g���v�Ƃ��������łȂ��A(4)�ł́A���R�c���܂ōl����̂ŁA��蕶�Ɂu�f�M�ω��v�Ƃ����q���g�͂���܂����A����ł��l������ł��܂��܂��B
(�C) �˒萔��k�Ƃ��܂��B�ŏ��A�s�X�g��C�ɂ́A�E�����ő傫��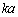 ��(�˂�)�e�����ƁA�������ő傫��
��(�˂�)�e�����ƁA�������ő傫��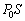 ����C���ɂ�����������āA�肠���Ă��܂��B
����C���ɂ�����������āA�肠���Ă��܂��B �͂̂荇���F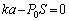
�� 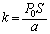 ......[��]�ŏ��̗̈�T�̋C��(�ȉ��A�C�̇T�Ƃ��܂�)�ɂ��āA��ԕ������F
......[��]�ŏ��̗̈�T�̋C��(�ȉ��A�C�̇T�Ƃ��܂�)�ɂ��āA��ԕ������F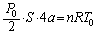 ����@
����@
(1)(��) �s�X�g��B���X�g�b�p�[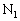 �𗣂��Ƃ�(�s�X�g��B�ƃX�g�b�p�[
�𗣂��Ƃ�(�s�X�g��B�ƃX�g�b�p�[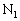 �̊Ԃ������R����0)�A�C�̇T��������P�C���x��
�̊Ԃ������R����0)�A�C�̇T��������P�C���x��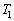 �Ƃ��āA�s�X�g��B�Ƃ˂ƃs�X�g��C���琬��n�ɓ������́A�C�̇T�������ɂ��E�����ő傫��
�Ƃ��āA�s�X�g��B�Ƃ˂ƃs�X�g��C���琬��n�ɓ������́A�C�̇T�������ɂ��E�����ő傫��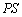 �����ƁA��C���ɂ�鍶�����ő傫��
�����ƁA��C���ɂ�鍶�����ő傫��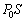 �����ŁA���̗��҂��͂̂荇�����A
�����ŁA���̗��҂��͂̂荇�����A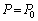
���̂Ƃ��̋C�̇T����ԕ������F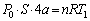 ����A
����A
�A���@���A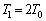 .......[��]
.......[��]
(�n) �X�C�b�`K����Ă���A�s�X�g��B���X�g�b�p�[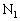 �𗣂��܂�(���̊Ԃ̕ω�����ϕω��ł�)��������t�Ƃ��āA�C�̇T���z�������M��
�𗣂��܂�(���̊Ԃ̕ω�����ϕω��ł�)��������t�Ƃ��āA�C�̇T���z�������M��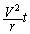
�C�̇T���̐��͕ω����Ă��Ȃ��̂ŁA�C�̇T�̂����d����0�C�̇T(�P���q���q���z�C�̂Ȃ̂���σ�����M��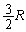 �ł�)�������G�l���M�[�̕ω��́A���x��
�ł�)�������G�l���M�[�̕ω��́A���x��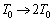 �ƕω������̂ŁA�@��p���āA
�ƕω������̂ŁA�@��p���āA �� 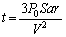 ......[��]
......[��]
(2)(�j) (1)�̌�A�s�X�g��B�Ƃ˂ƃs�X�g��C���琬��n�ɓ������́A�E�����̋C�̇T�������ɂ�����ƁA����������C���ɂ�����݂̂ł��B�s�X�g��B���������ړ������Ɩ�蕶�ɏ�����Ă���̂ŁA�����ł��邭�炢�̏��������x�������x�^�������ƍl����ƁA�ߒ�(2)�ɂ����Ă��A�s�X�g��B�Ƃ˂ƃs�X�g��C���琬��n�ɓ����͂̂荇�����������܂��B�]���āA�C�̇T��������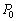 �ň��ɕۂ���Ă��āA�C�̇T���舳�ω������Ă��܂��B
�ň��ɕۂ���Ă��āA�C�̇T���舳�ω������Ă��܂��B �s�X�g��C���X�g�b�p�[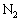 �ɐڐG�����Ƃ��A�C�̇T���̐���
�ɐڐG�����Ƃ��A�C�̇T���̐���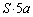 �ŁA���x��
�ŁA���x��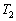 �Ƃ��āA�C�̇T����ԕ������F
�Ƃ��āA�C�̇T����ԕ������F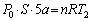 ����B
����B
�B���@���A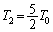 ......[��]
......[��]
(�z) �P���q���q���z�C�̂��舳������M��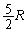 �ł��B�ߒ�(2)�ɂ����ċC�̇T�����x�́A
�ł��B�ߒ�(2)�ɂ����ċC�̇T�����x�́A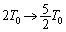 �ƕω����܂��B
�ƕω����܂��B �舳������M�̎���p����ƁA�ߒ�(2)�ɂ����ċC�̇T���z�������M���́A�@��p���āA
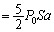 ......[��]
......[��]
(3)(�w) �˂̒�����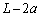 �ɒB�������_(�˂��k����
�ɒB�������_(�˂��k����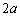 )�ŁA�C�̇T���̐���
)�ŁA�C�̇T���̐���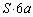 �ŁA������
�ŁA������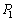 �C���x��
�C���x��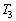 �Ƃ��āA
�Ƃ��āA �s�X�g��B�ɓ����͂̂荇���F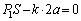 (�C)�̌��ʂ�p���āA
(�C)�̌��ʂ�p���āA ���̎��_�ł̋C�̇T����ԕ������F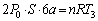 ����C
����C
�C���@���A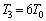 ......[��]
......[��]
(�g) �ߒ�(3)�ɂ����āA�s�X�g��C�̓X�g�b�p�[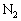 �ɉ��������Ă���̂ŁA�C�̇T�͑�C�ɑ��Ă��d���������A�˂ɑ��Ă̂��d�������܂��B
�ɉ��������Ă���̂ŁA�C�̇T�͑�C�ɑ��Ă��d���������A�˂ɑ��Ă̂��d�������܂��B �˂��k����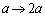 �ƕω�����̂ŁA�C�̇T���˂ɑ��Ă����d���A�����A�˂��~�����e���G�l���M�[�́A(�C)�̌��ʂ�p���āA
�ƕω�����̂ŁA�C�̇T���˂ɑ��Ă����d���A�����A�˂��~�����e���G�l���M�[�́A(�C)�̌��ʂ�p���āA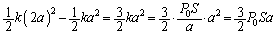
�C�̇T�����x��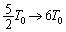 �ƕω�����̂ŁA���̊Ԃ̋C�̇T�������G�l���M�[�̕ω��́A
�ƕω�����̂ŁA���̊Ԃ̋C�̇T�������G�l���M�[�̕ω��́A 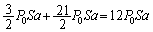 ......[��]
......[��]�Ȃ��A�ߒ�(3)�ɂ����āA�˂��k����x�Ƃ���(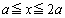 )�ƁA�C�̇T�̈���P���̐�
)�ƁA�C�̇T�̈���P���̐�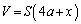 �̊Ԃɂ́A
�̊Ԃɂ́A
�s�X�g��B�ɓ����͂̂肠���F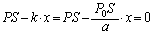
���x���������āA �� 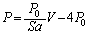 �@����D
�@����D
�Ƃ����W������܂��B 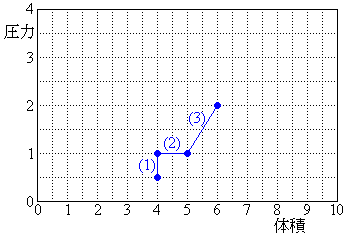 ��1�@�e�ߒ��ɂ����āA(�̐��C����)�̕ω����m�F���Ă����ƁA
��1�@�e�ߒ��ɂ����āA(�̐��C����)�̕ω����m�F���Ă����ƁA
�ߒ�(1)�ł́A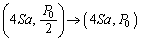 �@(��ϕω�)�ߒ�(2)�ł́A
�@(��ϕω�)�ߒ�(2)�ł́A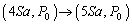 �@(�舳�ω�)�ߒ�(3)�ł́A
�@(�舳�ω�)�ߒ�(3)�ł́A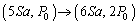 �ƕω����܂��B�D���A�O���t�͒����̈ꕔ���ɂȂ�܂��B��ԕω��̗l�q���O���t�ɕ\���ƉE�}�B
�ƕω����܂��B�D���A�O���t�͒����̈ꕔ���ɂȂ�܂��B��ԕω��̗l�q���O���t�ɕ\���ƉE�}�B
(4)(�`) �ߒ�(4)���f�M�ω��ŋC�̂̋z�������M����0�ł��B ��D���J����ƋC�̂͗̈�U�֘R��o���܂����A�̈�U�͐^��Ő^��ւ̖c��(���R�c��)�ł́A�C�̂��d�������܂���B�s�X�g��C���X�g�b�p�[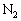 �ɐڐG�����܂܂Ȃ̂ŁA�C�̇T�͑�C�ɑ��Ă��d���������A�˂ɑ��Ă̂��d�������܂��B
�ɐڐG�����܂܂Ȃ̂ŁA�C�̇T�͑�C�ɑ��Ă��d���������A�˂ɑ��Ă̂��d�������܂��B
�˂��k����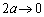 �ƕω�����̂ŁA�C�̇T���˂ɑ��Ă����d���A�����A�˂��~�����G�l���M�[�́A(3)�Ɠ��l�ɂ��āA
�ƕω�����̂ŁA�C�̇T���˂ɑ��Ă����d���A�����A�˂��~�����G�l���M�[�́A(3)�Ɠ��l�ɂ��āA ���ɂȂ�Ƃ������Ƃ́A�˂��e���G�l���M�[����o���ċC�̂ɑ����d��������(�C�̂��d�������ꂽ)�Ƃ������Ƃł��B
�ߒ�(4)�ɂ����āA�C�̇T�����x��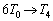 �ɂȂ����Ƃ��āA�C�̂������G�l���M�[�̕ω��́A
�ɂȂ����Ƃ��āA�C�̂������G�l���M�[�̕ω��́A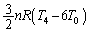
�M�͊w���@������A �@���A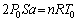 ������A
������A �� 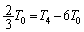 ��
�� 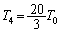 ......[��]
......[��]
(��) �˂����R���ɂ��ǂ����Ƃ��A�̈�T�C�̈�U�ɂ���C�̂��̐���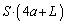 �C���̂Ƃ��̋C�̂����x��
�C���̂Ƃ��̋C�̂����x��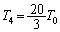 �C������
�C������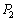 �Ƃ��āA
�Ƃ��āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B