京大物理'05年前期[1]
次の文を読んで、 には適した式を、 には適した数値を、それぞれ記せ。
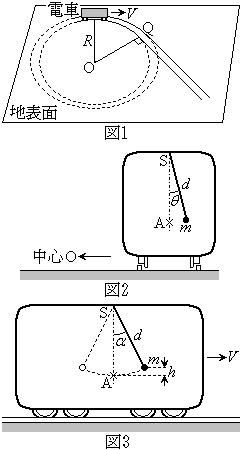 図1のように、水平な地表面上に敷かれたレールを電車が一定の速さVで動いているとする。このレールは、点Qの手前で点Oを中心とした半径Rの円弧状であり、点Qの先では点Qで円弧に接する直線状となっている。レールの幅、電車の幅、長さ、高さはいずれも、Rに比べて非常に小さいとする。以下の(1)〜(3)では電車は円弧状のレール上を動いているときについて、(4)では電車が直線状のレールを動いているときについて、車内での小物体の運動を考える。ここで、重力加速度の大きさをgとし、小物体の大きさと小物体に対する空気の抵抗はいずれも無視する。
図1のように、水平な地表面上に敷かれたレールを電車が一定の速さVで動いているとする。このレールは、点Qの手前で点Oを中心とした半径Rの円弧状であり、点Qの先では点Qで円弧に接する直線状となっている。レールの幅、電車の幅、長さ、高さはいずれも、Rに比べて非常に小さいとする。以下の(1)〜(3)では電車は円弧状のレール上を動いているときについて、(4)では電車が直線状のレールを動いているときについて、車内での小物体の運動を考える。ここで、重力加速度の大きさをgとし、小物体の大きさと小物体に対する空気の抵抗はいずれも無視する。
(1) 電車が点Qの手前の円弧状のレール上を走っているとき、図2のように、電車の天井の点Sから、質量の無視できる長さdの糸でつるされた質量mの小物体は、車内の観測者から見て静止していた。なお、図2はこの電車を進行方向から見たところであり、図の左方向が中心Oの方向である。また、点Aは電車が動いていないときの小物体の静止位置である。このとき、車内の観測者には、車内の小物体に大きさ ア の遠心力が働いているように見えるので、糸が鉛直線SAとなす角度θ は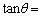 イ を満たす。また、糸の張力Tと重力
イ を満たす。また、糸の張力Tと重力 との比はθ のみを用いて、
との比はθ のみを用いて、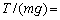 ウ と表される。
ウ と表される。 (2) 小物体が車内の観測者から見て動いているときでも、その速さがVに比べてじゅうぶんに小さければ、短い間に電車の加速度運動が小物体へ及ぼす影響は、大きさ ア の遠心力のみに現れると近似的に考えることができる。以下、この近似を使って考えることにする。この場合、車内の観測者から見て小物体には常に重力と大きさ ア の遠心力の合力が働くので、あたかも重力加速度の方向と大きさが変化したように見える。この見かけの重力加速度の大きさを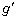 とすると、
とすると、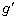 とgの比はθ のみを用いて表すことができて、
とgの比はθ のみを用いて表すことができて、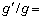 エ となる。
エ となる。 (3) 小物体を点Aから、車内の観測者から見て速さuで電車の進行方向に押し出した。この後、小物体は車内の観測者から見て円運動をした。この円運動の半径はdとθ を用いて表すと オ である。また、速さuはd,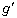 ,θ を用いて表すと
,θ を用いて表すと カ であり、円運動の周期はd,
カ であり、円運動の周期はd,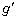 ,θ を用いて表すと キ となる。
,θ を用いて表すと キ となる。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難問なのですが、誘導に従って考えてゆけばゴールにたどりつけます。(3)のuと(4)のuが結びつけばよいのです。
 (1)(ア) 等速円運動している電車の加速度は
(1)(ア) 等速円運動している電車の加速度は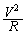 です。電車内の観測者から見て小物体に働く遠心力は、
です。電車内の観測者から見て小物体に働く遠心力は、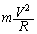 ......[答]
......[答](イ) 右図より、 ......[答]
......[答]
(ウ) 張力Tと見かけの重力 がつりあうから、
がつりあうから、 ......[答]
......[答]
(2)(エ) 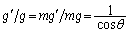 ......[答]
......[答]
(3)(オ) 電車内の観測者から見て、小物体は、Aを通り図2の糸の方向(つりあいのときの方向)と垂直な面内で等速円運動する。 円運動の半径は、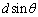 ......[答]
......[答] ∴  ......[答]
......[答] (キ) 円運動の周期を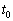 とし、円周の長さを考えて、
とし、円周の長さを考えて、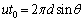
∴ 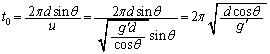 ......[答]
......[答]
∴ 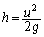 .......[答]
.......[答] (ケ) (2)の結果 ,(3)の結果
,(3)の結果 より、
より、 一方、図3より、
よって、
∴  ......[答]
......[答] (コ) 問題文の近似を行うと、
∴ 
1 ......[答]
(3)は、「見かけの重力」を重力のように考えて、糸に角度をつけて小物体に速度を与えると考えれば、円錐振り子になっていることがわかると思います。
(4)は、円錐振り子の円の接線方向の速度(等速円運動の速さ)が振動中心での速さになることに気づけばよいでしょう。振動を考える必要もなく、力学的エネルギー保存則の式を立てるのみで解決します。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 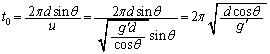 ......[答]
......[答]