���啨��'10�N[2]
�ȉ���(1)��(2)���@�@�ɂ͓K���������A���ꂼ��̉��ɋL������B�Ȃ��A�@�@�͂��ł��@�@�ŗ^����ꂽ���̂Ɠ�������\���B�܂��A��1�`��3�ł́A�w���ɂ��������āA�����ꂼ��̉��ɋL������B
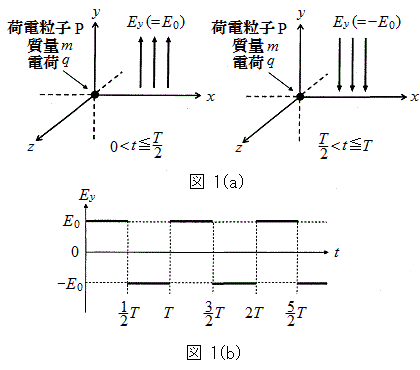 (1) �}1(a)�Ɏ����悤�ɁAxyz��Ԃɓd��
(1) �}1(a)�Ɏ����悤�ɁAxyz��Ԃɓd�� ���������Ă���B���̓d��́A�}1(b)�Ɏ����悤�ɁA������T�Ƃ��Ď��ԓI�ɕω����Ă���B�ŏ��̔������ɂ�y���̐��̌����ɑ傫��
���������Ă���B���̓d��́A�}1(b)�Ɏ����悤�ɁA������T�Ƃ��Ď��ԓI�ɕω����Ă���B�ŏ��̔������ɂ�y���̐��̌����ɑ傫�� �̓d�ꂪ�A���̔������ɂ�y���̕��̌����ɑ傫��
�̓d�ꂪ�A���̔������ɂ�y���̕��̌����ɑ傫��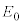 �̓d�ꂪ��������B��������d��́A��ԓI�ɂ͈�l�ł���B���ʂ�m�Ő��̓d��q�����דd���qP���A����t��
�̓d�ꂪ��������B��������d��́A��ԓI�ɂ͈�l�ł���B���ʂ�m�Ő��̓d��q�����דd���qP���A����t��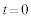 �Ō��_(
�Ō��_(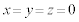 )�ɂ���B���̗��qP�́Ay�������̓d��ɂ���ĉ����x�^�������邪�A���̉^���̂悤����
)�ɂ���B���̗��qP�́Ay�������̓d��ɂ���ĉ����x�^�������邪�A���̉^���̂悤����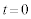 �ŗ��qP�ɗ^���鏉���x�ɂ���ĈقȂ�B�d�͂̉e���͖����ł���Ƃ���B
�ŗ��qP�ɗ^���鏉���x�ɂ���ĈقȂ�B�d�͂̉e���͖����ł���Ƃ���B
(1a) 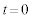 �ɂ����ė��qP�͌��_�ɐÎ~���Ă�����̂Ƃ���B
�ɂ����ė��qP�͌��_�ɐÎ~���Ă�����̂Ƃ���B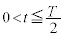 �̂Ƃ��ɂ́A���qP��y���̐��̌����ɉ��������B
�̂Ƃ��ɂ́A���qP��y���̐��̌����ɉ��������B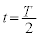 �ł̗��qP�̑��x��y����
�ł̗��qP�̑��x��y����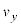 �ƍ��Wy�͂��ꂼ���@�C�@���@���@�ŕ\�����B
�ƍ��Wy�͂��ꂼ���@�C�@���@���@�ŕ\�����B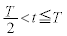 �̂Ƃ��ɂ́A���qP�́A
�̂Ƃ��ɂ́A���qP�́A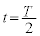 �ł̑��x��y�����@�C�@�ƍ��W�@���@�������l�Ƃ���y���̕��̌����ɉ��������B
�ł̑��x��y�����@�C�@�ƍ��W�@���@�������l�Ƃ���y���̕��̌����ɉ��������B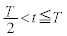 �̂Ƃ��A���qP�̑��x��y����
�̂Ƃ��A���qP�̑��x��y����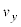 ������t�̊��Ƃ��ĕ\�����@�n�@�ƂȂ�B���̂Ƃ��̗��qP�̍��Wy������t�̊��Ƃ��ĕ\�����Ƃ��ł���B�����̌��ʂ���A
������t�̊��Ƃ��ĕ\�����@�n�@�ƂȂ�B���̂Ƃ��̗��qP�̍��Wy������t�̊��Ƃ��ĕ\�����Ƃ��ł���B�����̌��ʂ���A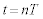 (
(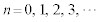 )�ł̗��qP�̑��x��y������0�ł��邪�A���qP�͎��Ԃ̌o�߂ƂƂ��Ɍ��_���痣��Ă������Ƃ��킩��B
)�ł̗��qP�̑��x��y������0�ł��邪�A���qP�͎��Ԃ̌o�߂ƂƂ��Ɍ��_���痣��Ă������Ƃ��킩��B
��1�@�ȏ�̌��ʂ����ƂɁA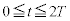 �ɂ����闱�qP�̑��x��y����
�ɂ����闱�qP�̑��x��y����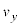 ������t�̊��Ƃ��ăO���t�Ɏ����B�O���t���ɂ�
������t�̊��Ƃ��ăO���t�Ɏ����B�O���t���ɂ�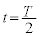 �ɂ����鑬�x��y����
�ɂ����鑬�x��y����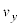 �̒l���L������B�܂��A
�̒l���L������B�܂��A �ɂ����闱�qP�̍��Wy�Ǝ���t�Ƃ̊W��\���Ȑ��̊T�v���O���t�Ɏ����B�������A�O���t����
�ɂ����闱�qP�̍��Wy�Ǝ���t�Ƃ̊W��\���Ȑ��̊T�v���O���t�Ɏ����B�������A�O���t����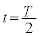 �ɂ�������Wy�̒l���L������K�v�͂Ȃ��B
�ɂ�������Wy�̒l���L������K�v�͂Ȃ��B
(1b)  �ɂ����āA���qP�̑��x��x����
�ɂ����āA���qP�̑��x��x����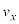 ��z����
��z����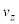 ��
��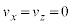 �Ƃ��āA���x��y����
�Ƃ��āA���x��y����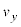 ��K�Ȓl�ɂ���A���Ԃ��o�߂��Ă����qP�����_���牓������Ă����Ȃ��悤�ɂ��邱�Ƃ��ł���B���̂Ƃ��A
��K�Ȓl�ɂ���A���Ԃ��o�߂��Ă����qP�����_���牓������Ă����Ȃ��悤�ɂ��邱�Ƃ��ł���B���̂Ƃ��A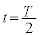 �����
�����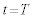 �ł̗��qP�̍��Wy���Ƃ���
�ł̗��qP�̍��Wy���Ƃ���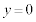 �ɂȂ�A�܂�
�ɂȂ�A�܂�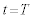 �ł̑��x��y����
�ł̑��x��y����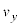 ��
��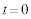 �̂Ƃ��Ɠ����l�ł���B���̏����́A
�̂Ƃ��Ɠ����l�ł���B���̏����́A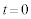 �ł̗��qP�̑��x��y����
�ł̗��qP�̑��x��y����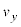 ���@�j�@�̏ꍇ�ɖ��������B���̂Ƃ��A
���@�j�@�̏ꍇ�ɖ��������B���̂Ƃ��A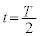 �ɂ����闱�qP�̑��x��y����
�ɂ����闱�qP�̑��x��y����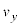 �́|�@�j�@�ƂȂ�B
�́|�@�j�@�ƂȂ�B 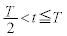 �̂Ƃ��ɂ́A���qP��
�̂Ƃ��ɂ́A���qP��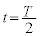 �ł̑��x�ƍ��W�������l�Ƃ���y���̕��̌����ɉ��������B
�ł̑��x�ƍ��W�������l�Ƃ���y���̕��̌����ɉ��������B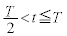 �̂Ƃ��̗��qP�̑��x��y����
�̂Ƃ��̗��qP�̑��x��y����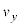 ������t�̊��Ƃ��ĕ\�����@�z�@�ƂȂ�B���̂Ƃ��̗��qP�̍��Wy������t�̊��Ƃ��ĕ\�����Ƃ��ł���B
������t�̊��Ƃ��ĕ\�����@�z�@�ƂȂ�B���̂Ƃ��̗��qP�̍��Wy������t�̊��Ƃ��ĕ\�����Ƃ��ł���B
��2�@�ȏ�̌��ʂ����ƂɁA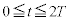 �ɂ����闱�qP�̑��x��y����
�ɂ����闱�qP�̑��x��y����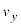 ������t�̊��Ƃ��ăO���t�Ɏ����B�O���t���ɂ�
������t�̊��Ƃ��ăO���t�Ɏ����B�O���t���ɂ�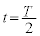 �ɂ����鑬�x��y����
�ɂ����鑬�x��y����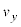 �̒l���L������B�܂��A
�̒l���L������B�܂��A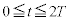 �ɂ����闱�qP�̍��Wy�Ǝ���t�Ƃ̊W��\���Ȑ��̊T�v���O���t�Ɏ����B�������A�O���t����
�ɂ����闱�qP�̍��Wy�Ǝ���t�Ƃ̊W��\���Ȑ��̊T�v���O���t�Ɏ����B�������A�O���t����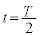 �ɂ�������Wy�̒l���L������K�v�͂Ȃ��B
�ɂ�������Wy�̒l���L������K�v�͂Ȃ��B
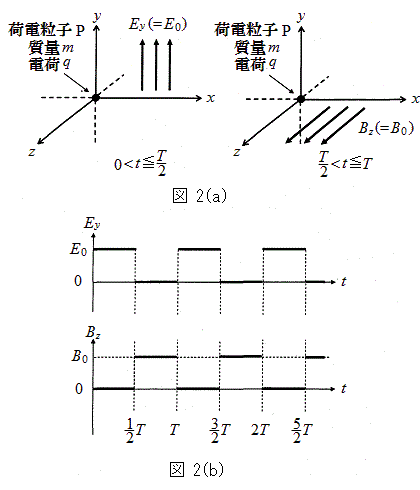 (2) �}2(a)�Ɏ����悤�ɁAxyz��Ԃɓd��
(2) �}2(a)�Ɏ����悤�ɁAxyz��Ԃɓd��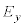 �܂��͎���
�܂��͎���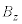 ����������B�����̓d��Ǝ���́A�}2(b)�Ɏ����悤�ɁA������T�Ƃ��Ď��ԓI�ɕω����Ă���B�ŏ��̔������ɂ�y���̐��̌����ɑ傫��
����������B�����̓d��Ǝ���́A�}2(b)�Ɏ����悤�ɁA������T�Ƃ��Ď��ԓI�ɕω����Ă���B�ŏ��̔������ɂ�y���̐��̌����ɑ傫��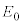 �̓d��݂̂��A���̔������ɂ�z���̐��̌����Ɏ������x�̑傫��
�̓d��݂̂��A���̔������ɂ�z���̐��̌����Ɏ������x�̑傫��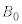 �̎���݂̂���������B��������d��⎥��́A��ԓI�ɂ͈�l�ł���B���ʂ�m�Ő��̓d��q�������qP��
�̎���݂̂���������B��������d��⎥��́A��ԓI�ɂ͈�l�ł���B���ʂ�m�Ő��̓d��q�������qP��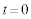 �Ō��_(
�Ō��_(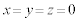 )�ɂ���B
)�ɂ���B�ŏ��ɁA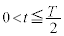 �̂Ƃ��̗��qP�̉^����(1b)�̏ꍇ�Ɠ����ɂȂ�悤�ɁA
�̂Ƃ��̗��qP�̉^����(1b)�̏ꍇ�Ɠ����ɂȂ�悤�ɁA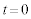 �ł̗��qP�̑��x��x����
�ł̗��qP�̑��x��x����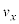 ��z����
��z����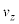 ��
��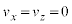 �Ƃ��āA���x��y����
�Ƃ��āA���x��y����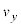 ���@�j�@�Ƃ���B
���@�j�@�Ƃ���B
����A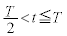 �̂Ƃ��ɂ́A����̉e�����đ傫�����@�w�@�̃��[�����c�͂����qP�ɍ�p����B���̂��߁A���qP��xy���ʓ��ʼn~�^�����n�߂�B���̉~�^���̒��S��x����ɂ���A����x���W���@�g�@�ŗ^������B���̂Ƃ��A�~�^���̔��a�͎������x�̑傫��
�̂Ƃ��ɂ́A����̉e�����đ傫�����@�w�@�̃��[�����c�͂����qP�ɍ�p����B���̂��߁A���qP��xy���ʓ��ʼn~�^�����n�߂�B���̉~�^���̒��S��x����ɂ���A����x���W���@�g�@�ŗ^������B���̂Ƃ��A�~�^���̔��a�͎������x�̑傫��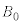 �ɉ����ĕω����邪�A
�ɉ����ĕω����邪�A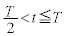 �̊Ԃɗ��qP���^������O�Ղ̒������@�`�@�ƂȂ�A�������x�̑傫��
�̊Ԃɗ��qP���^������O�Ղ̒������@�`�@�ƂȂ�A�������x�̑傫��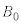 �ɂ��Ȃ��B
�ɂ��Ȃ��B
���܁A�������x�̑傫��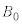 ���@���@�ɑI�ԂƁA���qP�́A
���@���@�ɑI�ԂƁA���qP�́A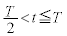 �̊Ԃ�xy���ʓ��ʼn~�O����������A
�̊Ԃ�xy���ʓ��ʼn~�O����������A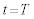 �ɂ����čĂ�
�ɂ����čĂ�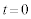 �̂Ƃ��Ɠ������x��y����
�̂Ƃ��Ɠ������x��y����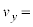 �@�j�@�ƍ��W
�@�j�@�ƍ��W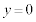 �����悤�ɂ��邱�Ƃ��ł���B���̂Ƃ��A���qP��x���W���@�k�@�ƂȂ�B����ȍ~��
�����悤�ɂ��邱�Ƃ��ł���B���̂Ƃ��A���qP��x���W���@�k�@�ƂȂ�B����ȍ~��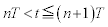 (
(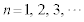 )�̂Ƃ��ɂ́A���qP�́Ay�������ɂ�
)�̂Ƃ��ɂ́A���qP�́Ay�������ɂ�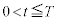 �̂Ƃ��Ɠ����^�����s���Ax�������ɂ͌��_���痣��Ă����B
�̂Ƃ��Ɠ����^�����s���Ax�������ɂ͌��_���痣��Ă����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�d���C�̊�{�ƁA�������x�^���A�~�^���Ƃ̗Z�����ł��B�ȉ��̖�1�C��2�ł́A���x��y����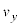 �����łȂ�y���W�ɂ��Ă��v�Z�������߂���ŃO���t�������Ă��܂����A����I�ɂ́A�v�Z�Ȃ��Ŋ��o�I�ɃO���t��`�������Ƃ���ł��B
�����łȂ�y���W�ɂ��Ă��v�Z�������߂���ŃO���t�������Ă��܂����A����I�ɂ́A�v�Z�Ȃ��Ŋ��o�I�ɃO���t��`�������Ƃ���ł��B
�ׂ������Ƃł����A��2��蕶���́u�O���t����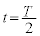 �ɂ�������Wy�̒l���L������K�v�͂Ȃ��B�v��
�ɂ�������Wy�̒l���L������K�v�͂Ȃ��B�v��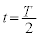 �́A��蕶����
�́A��蕶����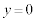 �Ǝw�肳��Ă���̂ŁA
�Ǝw�肳��Ă���̂ŁA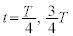 �̊ԈႢ�ł͂Ȃ����Ǝv���܂��B
�̊ԈႢ�ł͂Ȃ����Ǝv���܂��B
(��)����������Ηǂ��̂��A���X�Y�ނ����m��܂���B�~�^���̔����̒���(�`)��2�ʂ�ɕ\����邱�Ƃ𗘗p���܂��B
(1)(1a)(�C)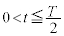 �ɂ����āA y�����������d��
�ɂ����āA y�����������d��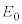 ���d��q�������qP�ɁAy���������ɑ傫��
���d��q�������qP�ɁAy���������ɑ傫��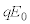 �������y�ڂ��܂�(�d�E���Q��)�B���qP�������x��a�Ƃ��āA�^���������F
�������y�ڂ��܂�(�d�E���Q��)�B���qP�������x��a�Ƃ��āA�^���������F 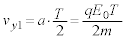 ......[��]
......[��]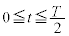 �ɂ����āA���x��y����
�ɂ����āA���x��y����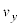 ������t�̊��Ƃ��ĕ\���ƁA
������t�̊��Ƃ��ĕ\���ƁA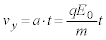 �@����@
�@����@y���W������t�̊��Ƃ��ĕ\���ƁA
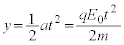 �@����A
�@����A
(��) �A���A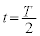 �ɂ����闱�q��y���W
�ɂ����闱�q��y���W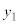 �́A
�́A 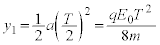 ......[��]
......[��]
(�n) 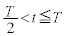 �ɂ����ẮA�d���̌������t�ɂȂ�A�����x��
�ɂ����ẮA�d���̌������t�ɂȂ�A�����x��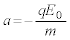 �ƂȂ�̂ŁA���qP������t�ɂ��������x��y����
�ƂȂ�̂ŁA���qP������t�ɂ��������x��y����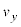 �́A
�́A 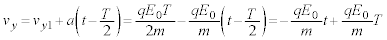 ......[��]�@����B
......[��]�@����B����t�ɂ�����y���W�́A
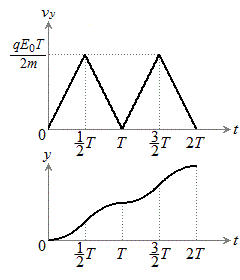 ��1�@
��1�@ �ɂ�����
�ɂ�����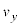 -t �O���t�́A
-t �O���t�́A ��
��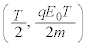 �����Ԑ����ł��B
�����Ԑ����ł��B �ɂ�����
�ɂ�����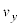 -t �O���t�́A
-t �O���t�́A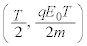 �C
�C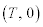 �����Ԑ����ł��B�Ȍ�A
�����Ԑ����ł��B�Ȍ�A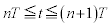 (
(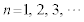 )�ɂ�����
)�ɂ�����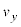 -t�̃O���t�́A
-t�̃O���t�́A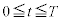 �ɂ�����O���t�̌J��Ԃ��ɂȂ�܂��B
�ɂ�����O���t�̌J��Ԃ��ɂȂ�܂��B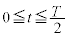 �ɂ�����y-t �O���t�́A
�ɂ�����y-t �O���t�́A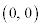 �_�Ƃ��鉺�ɓʂȕ������A
�_�Ƃ��鉺�ɓʂȕ������A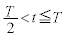 �ɂ�����y-t �O���t�́A
�ɂ�����y-t �O���t�́A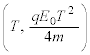 �_�Ƃ����ɓʂȕ������ł��B�Ȍ�A
�_�Ƃ����ɓʂȕ������ł��B�Ȍ�A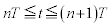 �ɂ�����y-t �O���t�́A
�ɂ�����y-t �O���t�́A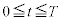 �ɂ�����O���t�s�ړ������O���t�ɂȂ�܂��B
�ɂ�����O���t�s�ړ������O���t�ɂȂ�܂��B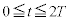 �ɂ����闼�O���t��}������ƁA�E�}�����B
�ɂ����闼�O���t��}������ƁA�E�}�����B(1b)(�j) 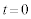 �ɂ��������x��y������
�ɂ��������x��y������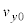 �Ƃ��āA����t (
�Ƃ��āA����t (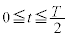 )�ɂ�����y���W�́A
)�ɂ�����y���W�́A
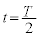 �ɂ�����y���W��
�ɂ�����y���W��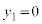 �ɂȂ�Ƃ��āA
�ɂȂ�Ƃ��āA�� 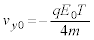 ......[��]
......[��]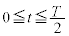 �ɂ����āA
�ɂ����āA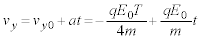 �ƂȂ�̂ŁA���̂Ƃ��A
�ƂȂ�̂ŁA���̂Ƃ��A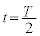 �ɂ����闱�qP�����x��y����
�ɂ����闱�qP�����x��y����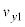 �ɂ��āA
�ɂ��āA ���A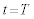 �ɂ�����y���W
�ɂ�����y���W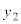 ���A��蕶�ɂ���悤�ɁA
���A��蕶�ɂ���悤�ɁA �ƂȂ�܂��B
(�z) 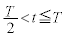 �ɂ��������x��y����
�ɂ��������x��y����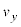 �́A�����x��
�́A�����x��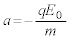 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA 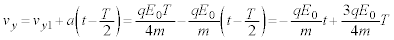 ......[��]
......[��]
 ��2�@
��2�@ �ɂ��������x��y������
�ɂ��������x��y������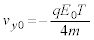 �ɂȂ�ƁA
�ɂȂ�ƁA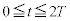 �ɂ�����
�ɂ�����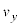 -t �O���t�́A��1��
-t �O���t�́A��1��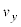 -t �O���t��
-t �O���t��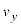 ����������
����������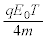 �������s�ړ������O���t�ɂȂ�܂��B�܂��A
�������s�ړ������O���t�ɂȂ�܂��B�܂��A�Ȍ�A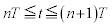 (
(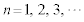 )�ɂ�����y-t �O���t�́A
)�ɂ�����y-t �O���t�́A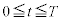 �ɂ�����O���t�̌J��Ԃ��ɂȂ�܂��B
�ɂ�����O���t�̌J��Ԃ��ɂȂ�܂��B
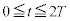 �ɂ����闼�O���t��}������ƁA�E�}�����B
�ɂ����闼�O���t��}������ƁA�E�}�����B
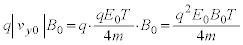 ......[��]
......[��]
(�g) ���q�ɂ͒��S���������[�����c���̂ݓ����A�~�̐ڐ��̕����ɂ����������Ȃ��̂ŁA���q�̉^���������~�^���ł��B�~�^�������a��r�Ƃ��āA���q���^���������́A �� 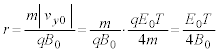 �~�^���̒��S��x���W��r�ɓ������A
�~�^���̒��S��x���W��r�ɓ������A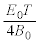 ......[��]
......[��]
(�`) ��������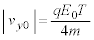 ������
������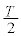 �^������̂ŁA�O�Ղ������́A
�^������̂ŁA�O�Ղ������́A 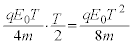 ......[��]
......[��]
(��) ����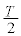 �ŗ��q����������̂�(�`)�̌��ʂ�
�ŗ��q����������̂�(�`)�̌��ʂ�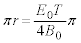 �ɓ������A
�ɓ������A �� 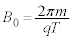 ......[��]
......[��]
(�k) �~�O��������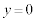 �ƂȂ����Ƃ���x���W�́A
�ƂȂ����Ƃ���x���W�́A 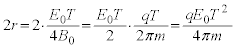 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �_�Ƃ����ɓʂȕ������ł��B�Ȍ�A
�_�Ƃ����ɓʂȕ������ł��B�Ȍ�A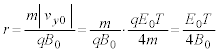
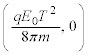 �𒆐S�Ƃ����a
�𒆐S�Ƃ����a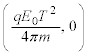 �ɓ��B���܂��B�Ȍ�Ax�������Ɍ��_���痣��čs���Ȃ���Ay�������ɂ�
�ɓ��B���܂��B�Ȍ�Ax�������Ɍ��_���痣��čs���Ȃ���Ay�������ɂ�