磁性体における磁界、磁束密度
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
磁荷率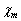 の磁性体中における磁界を
の磁性体中における磁界を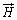 ,磁化を
,磁化を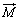 として、
として、
磁束密度を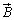 として、
として、
ここで、μは透磁率と言い、真空の透磁率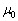 との間に、
との間に、
という関係がある。
磁性体が持つ磁化を、電気における分極のように考えることができます(誘電体がある場合のガウスの法則を参照)。
原点Oに位置する半径aの微小な円周上を電流Iが流れるとき、充分に離れた位置P、即ち、円形電流から距離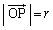 (
(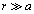 )だけ離れた位置Pにおける磁位Vは、
)だけ離れた位置Pにおける磁位Vは、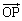 がz軸(円の中心を通り、円が乗っている平面に垂直な軸)となす角をθ として、
がz軸(円の中心を通り、円が乗っている平面に垂直な軸)となす角をθ として、
で与えられます(磁気双極子を参照)。ここで、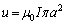 は磁気双極子モーメントの大きさです。
は磁気双極子モーメントの大きさです。
円筒座標で考えると(座標系を参照)、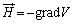 より、磁界のr成分
より、磁界のr成分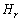 ,θ 成分
,θ 成分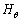 は、
は、
これらは、大きさpの電気双極子モーメントをもつ電気双極子が位置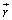 (
(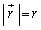 ,z軸と
,z軸と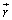 のなす角をθ とする)に作る電界
のなす角をθ とする)に作る電界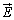 のr方向成分
のr方向成分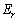 ,θ 方向成分
,θ 方向成分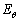 が、
が、
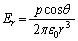 ,
,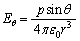
磁化ベクトル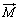 は、磁気双極子モーメントの密度N、つまり、単位体積当たりの磁気双極子の密度Nと磁気双極子モーメント
は、磁気双極子モーメントの密度N、つまり、単位体積当たりの磁気双極子の密度Nと磁気双極子モーメント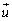 (大きさがuで、向きは円形電流が右ねじの回る向きに流れるとして、右ねじの進む向き)の積
(大きさがuで、向きは円形電流が右ねじの回る向きに流れるとして、右ねじの進む向き)の積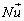 として定義されます。密度Nの単位は[
として定義されます。密度Nの単位は[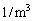 ],磁気双極子モーメント
],磁気双極子モーメント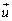 の単位は、
の単位は、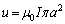 の単位を考えて、
の単位を考えて、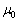 が[
が[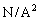 ],Iが[A],
],Iが[A],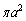 が[
が[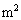 ]で、
]で、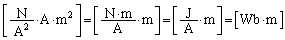 ,より、磁化の単位は、
,より、磁化の単位は、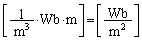 となります。
となります。
ここで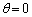 の方向(z軸、つまり双極子モーメントの方向)、
の方向(z軸、つまり双極子モーメントの方向)、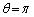 の方向を考えると、
の方向を考えると、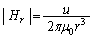 ,
,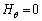 より、磁界の方向と双極子モーメント
より、磁界の方向と双極子モーメント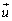 の方向は一致します。常磁性体、強磁性体に磁界
の方向は一致します。常磁性体、強磁性体に磁界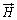 をかけると、磁化ベクトル
をかけると、磁化ベクトル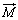 は磁界
は磁界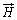 と同じ向きとなり、
と同じ向きとなり、
と書けます。比例定数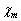 は磁化率で、常磁性体、強磁性体では、
は磁化率で、常磁性体、強磁性体では、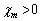 です。
です。
反磁性体では双極子モーメントの向きと磁界の向きは正反対の向きになり、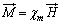 において、
において、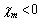 です(磁性体を参照)。
です(磁性体を参照)。
磁化率の単位は、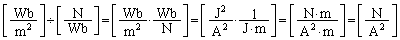 (真空の透磁率
(真空の透磁率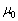 と同じ単位)
と同じ単位)
電荷QからQ本伸びるとして電束を考えた(ガウスの法則の一般化を参照)ように、磁気でも、磁荷mからm本の磁束が伸びると考えます。磁束の単位も磁荷の磁気量と同じく[Wb]です。磁束を磁束が貫く面の面積で割ったものを磁束密度と言います。磁束密度の単位は、磁化と同じく、[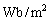 ]です。[
]です。[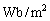 ]を一つにまとめて[T](テスラ)とします。
]を一つにまとめて[T](テスラ)とします。
真空中で、磁界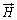 が存在する場所における磁束密度
が存在する場所における磁束密度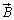 は、
は、
となります。
ここに磁性体を置くと、磁性体の中では、磁性体内の磁化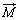 の分だけ磁力線の本数が減り、磁界が弱まります。磁性体内部の磁界が
の分だけ磁力線の本数が減り、磁界が弱まります。磁性体内部の磁界が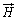 のとき、磁力線の本数分の磁束密度は
のとき、磁力線の本数分の磁束密度は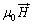 ,これと磁化
,これと磁化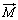 を合わせた磁束密度
を合わせた磁束密度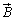 は、
は、
となります。ここで、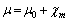 をこの磁性体の透磁率と言います。つまり、磁性体内では、
をこの磁性体の透磁率と言います。つまり、磁性体内では、
となります。透磁率の単位は[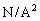 ]です。
]です。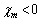 ということがあり得る(反磁性体の場合)ので、透磁率は、誘電率とは異なり、
ということがあり得る(反磁性体の場合)ので、透磁率は、誘電率とは異なり、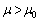 とは限りません。
とは限りません。
磁界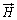 に関する、真空中における微分型のガウスの法則:
に関する、真空中における微分型のガウスの法則:
は、磁性体中でも、やはり単一磁荷は存在せず、円形電流の作る磁気双極子が単位になっているので、磁束密度について、
となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。