磁気におけるガウスの法則
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
磁気における微分型のガウスの法則：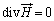
電気と同様に、磁気においても、単一磁荷が存在すると仮定して、一般化されたガウスの法則を考えます。
基礎事項については、磁界、磁力線を参照してください。
真空中で原点Oに磁荷mが置かれているとき、Oを中心とする半径rの球面上の磁界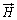
は、
と考えられます(磁気におけるクーロンの法則を参照)。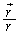
は、原点と球面上の点(位置ベクトル：
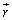)を結ぶ方向の単位ベクトルです。
原点Oを取り囲む任意の閉曲面Uについて、閉曲面上の各点における磁界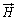
の面積分を考えると、
複数の単一磁荷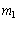
，
，･･･，
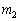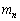が存在する場合には、電気の場合と同様(複数の電荷が存在する場合のガウスの法則を参照)にして、
しかしながら、単一磁荷の存在は否定されているので、空間内には同じ大きさの磁荷が正負必ずペアで存在し、この右辺の和はゼロです。
よって、ガウスの定理により、左辺の閉曲面U上の面積分を、閉曲面Uで囲まれた領域Vの体積分に変換すると、
閉曲面U，つまり、領域Vは空間内に任意に取れるので、
これが、磁気における微分型のガウスの法則となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理基礎事項TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
