������w2008�N�O�������������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 [1]�@����m�̔������C�̂Ȃ����炩�Ȑ����ʏ�ɐÎ~���Ă����Ƃ���B���̔����A����0����ړ������n�߂Ă��傤�ǎ���T�ɋ���L�������ꂽ�n�_��ʉ߂����邱�Ƃ��l���悤�BA�CB�CC��3�l�����ꂼ��ʁX�̗͂̉����������Ĕ����ړ��������B�`�̔��͍ŏ�����Ō�܂ň��̉����x�ʼn^�������BB�̔��͋���
[1]�@����m�̔������C�̂Ȃ����炩�Ȑ����ʏ�ɐÎ~���Ă����Ƃ���B���̔����A����0����ړ������n�߂Ă��傤�ǎ���T�ɋ���L�������ꂽ�n�_��ʉ߂����邱�Ƃ��l���悤�BA�CB�CC��3�l�����ꂼ��ʁX�̗͂̉����������Ĕ����ړ��������B�`�̔��͍ŏ�����Ō�܂ň��̉����x�ʼn^�������BB�̔��͋���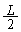 �̒��Ԓn�_�܂ň��̉����x�ʼn������A���Ԓn�_�ȍ~�͂��̎��̑��x�œ����x�^���������BC�͂˂�p���Ĉړ��������B�}1�̂悤�ɁA�˂����R���̏�ԂŔ����S�[���n�_�ɂ���悤�ɃZ�b�g���A��������˂�L�����k�߂ď���0�ŗ������BA�CB�CC�S�Ă̏ꍇ�ɂ����āA���͎���0�ŐÎ~������Ԃ��瓮���n�߁A�꒼����������ɐi�݁A����T�ɃX�^�[�g�n�_���瓯������L�������ꂽ�n�_��ʉ߂����B
�̒��Ԓn�_�܂ň��̉����x�ʼn������A���Ԓn�_�ȍ~�͂��̎��̑��x�œ����x�^���������BC�͂˂�p���Ĉړ��������B�}1�̂悤�ɁA�˂����R���̏�ԂŔ����S�[���n�_�ɂ���悤�ɃZ�b�g���A��������˂�L�����k�߂ď���0�ŗ������BA�CB�CC�S�Ă̏ꍇ�ɂ����āA���͎���0�ŐÎ~������Ԃ��瓮���n�߁A�꒼����������ɐi�݁A����T�ɃX�^�[�g�n�_���瓯������L�������ꂽ�n�_��ʉ߂����B
�T�@C���p�����˂̂˒萔k��m�CT��p���ĕ\���B
�U�@�`�CB�CC���ꂼ��̏ꍇ�ɂ��āA���̑���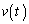 ������t (
������t ( )�̊��Ƃ��ăO���t�ɂ��A�e�X�̏ꍇ�̎���T�ɂ����鑬��
)�̊��Ƃ��ăO���t�ɂ��A�e�X�̏ꍇ�̎���T�ɂ����鑬��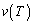 ��T�CL��p���ĕ\���B
��T�CL��p���ĕ\���B
�V�@A�CB�CC���ꂼ��̏ꍇ�ɂ��āA����T�܂łɔ��ɂ����d����m�CT�CL��p���ĕ\���A�ǂ̏ꍇ�ł��d�������Ȃ�������������B�܂����ꂼ��̏ꍇ�ɂ��āA���ɂ����d���ƇU�ŋ��߂�����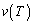 �Ƃ̊W�����߂�B
�Ƃ̊W�����߂�B
�W�@����Î~������Ԃ��瓮�����n�߁A�ŏ��̎d���ł��傤�ǎ���T�ɋ���L�������ꂽ�Ƃ����ʉ߂����邽�߂̗͂̉����������߂����B�������A���ɉ����邱�Ƃ̂ł���ő�̗͂�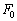 �Ƃ��A
�Ƃ��A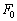 ��A�CB�CC�̉������ǂ̗͂����傫���Ƃ���B�܂��^���̌����Ƌt�����̗͂������邱�Ƃ͂Ȃ��Ƃ���B���ɂ���d�����ŏ��̏ꍇ�ɂ��āA���ɉ�������
��A�CB�CC�̉������ǂ̗͂����傫���Ƃ���B�܂��^���̌����Ƌt�����̗͂������邱�Ƃ͂Ȃ��Ƃ���B���ɂ���d�����ŏ��̏ꍇ�ɂ��āA���ɉ�������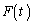 �̎��ԕω����O���t�ɂ��A����T�܂łɔ��ɂ����d������B
�̎��ԕω����O���t�ɂ��A����T�܂łɔ��ɂ����d������B [��]
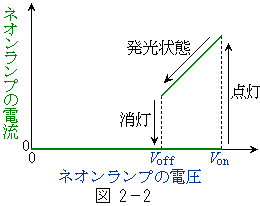
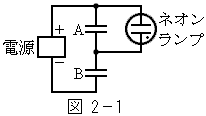 [2]�@�}2�|1�̂悤�ɁA�d�������R�ɕς����钼���d���ƃR���f���T�[A����уR���f���T�[B��ɂȂ��A�R���f���T�[A�ƕ���Ƀl�I�������v���Ȃ��B���̃l�I�������v�͐}2�|2�Ɏ����d���|�d�������������A�[�q�Ԃɂ�����d����
[2]�@�}2�|1�̂悤�ɁA�d�������R�ɕς����钼���d���ƃR���f���T�[A����уR���f���T�[B��ɂȂ��A�R���f���T�[A�ƕ���Ƀl�I�������v���Ȃ��B���̃l�I�������v�͐}2�|2�Ɏ����d���|�d�������������A�[�q�Ԃɂ�����d����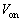 �ɒB����Ɠ_������B�_�������l�I�������v�́A�d����
�ɒB����Ɠ_������B�_�������l�I�������v�́A�d����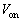 ��������Ă������𑱂��邪�A�d����
��������Ă������𑱂��邪�A�d����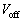 �܂ʼn�����Ə�������B�Ȃ��A�l�I�������v�̓d�C�e�ʂ͖����ł�����̂Ƃ��A�R���f���T�[A�CB�̓d�C�e�ʂ����ꂼ��
�܂ʼn�����Ə�������B�Ȃ��A�l�I�������v�̓d�C�e�ʂ͖����ł�����̂Ƃ��A�R���f���T�[A�CB�̓d�C�e�ʂ����ꂼ��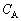 �C
�C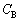 �ŕ\���B
�ŕ\���B
�T�@���ׂẴR���f���T�[����d��������A�d���d��V��0���班�����グ�Ă����ƁA����d��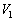 �Ńl�I�������v���_�����A���̌�A���������B�ȉ��̖�ɓ�����B�������A����
�Ńl�I�������v���_�����A���̌�A���������B�ȉ��̖�ɓ�����B�������A���� �C
�C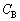 �C
�C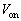 �C
�C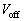 ��p���ĕ\���B�܂��A�l�I�������v���_�����Ă����������܂ł̊ԁA�d���d���͈��ł�����̂Ƃ��Ă悢�B
��p���ĕ\���B�܂��A�l�I�������v���_�����Ă����������܂ł̊ԁA�d���d���͈��ł�����̂Ƃ��Ă悢�B (1) ���̂Ƃ��̓d���d��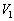 �����߂�B
�����߂�B (2) �_�����O�ɃR���f���T�[A�CB�ɒ~�����Ă����Ód�G�l���M�[�����ꂼ��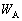 �C
�C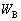 �Ƃ����A��������ɃR���f���T�[A�CB�ɒ~�����Ă���Ód�G�l���M�[�����ꂼ��
�Ƃ����A��������ɃR���f���T�[A�CB�ɒ~�����Ă���Ód�G�l���M�[�����ꂼ��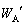 �C
�C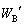 �Ƃ����B���̊Ԃ̐Ód�G�l���M�[�̕ω�
�Ƃ����B���̊Ԃ̐Ód�G�l���M�[�̕ω�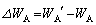 �����
�����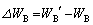 �����߂�B
�����߂�B (3) �d���́A�d�����ŕ��ɂ��琳�ɂ֓d�ׂ��^�Ԃ��Ƃɂ��A�l�I�������v����уR���f���T�[�ɃG�l���M�[���������Ă���B�܂��A�l�I�������v���_�����Ă����������܂ł̊Ԃɓd�����^�d�ׂ̗ʂ́A���̊ԂɃR���f���T�[B�ɐV���ɒ~����ꂽ�d�ׂ̗ʂƓ������B�l�I�������v���_�����Ă����������܂ł̊Ԃɓd�������������G�l���M�[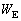 �����߂�B
�����߂�B (4) �_�����Ă����������܂ł̊ԂɃl�I�������v�������M�Ƃ��Ď���ꂽ�G�l���M�[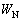 �����߂�B
�����߂�B
�U�@�l�I�������v�̏�����A����ɓd���d��V��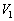 ���班�����グ�Ă����ƁA����d��
���班�����グ�Ă����ƁA����d��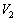 �Ńl�I�������v���Ăѓ_�����A���̌�A���������B�ȉ��̖�ɓ�����B
�Ńl�I�������v���Ăѓ_�����A���̌�A���������B�ȉ��̖�ɓ�����B  (1) ��T�ɂ����āA�_�����Ă����������܂ł̊ԂɃl�I�������v��ʉ߂����d�ׂ̗ʂ�Q�Ƃ���B�d���d��V��
(1) ��T�ɂ����āA�_�����Ă����������܂ł̊ԂɃl�I�������v��ʉ߂����d�ׂ̗ʂ�Q�Ƃ���B�d���d��V��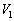 ����
����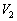 �ɒB����܂ł̊ԁA�R���f���T�[A�ɂ�����d��
�ɒB����܂ł̊ԁA�R���f���T�[A�ɂ�����d��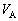 ��
��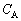 �C
�C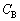 �CQ�CV��p���ĕ\���B�������A���̊ԁA�l�I�������v�ɓd��������邱�Ƃ͂Ȃ����߁A�}2�|1�̉�H�͐}2�|3�̉�H�Ɠ����ł���B�܂��A�d�ׂ��R���f���T�[��ʂ蔲���邱�Ƃ͂Ȃ����߁A�R���f���T�[A�CB�ɒ~�����Ă���d�ׂ����ꂼ��
�CQ�CV��p���ĕ\���B�������A���̊ԁA�l�I�������v�ɓd��������邱�Ƃ͂Ȃ����߁A�}2�|1�̉�H�͐}2�|3�̉�H�Ɠ����ł���B�܂��A�d�ׂ��R���f���T�[��ʂ蔲���邱�Ƃ͂Ȃ����߁A�R���f���T�[A�CB�ɒ~�����Ă���d�ׂ����ꂼ��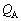 �C
�C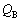 �Ƃ����A�R���f���T�[A�̉����̋ɔƃR���f���T�[B�̏㑤�̋ɔ��Ȃ��������ɒ~����ꂽ�����̓d�ׂ̗�
�Ƃ����A�R���f���T�[A�̉����̋ɔƃR���f���T�[B�̏㑤�̋ɔ��Ȃ��������ɒ~����ꂽ�����̓d�ׂ̗�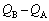 ��V�ɂ�炸���ł���AQ�Ɠ��������Ƃ�p���Ă悢�B
��V�ɂ�炸���ł���AQ�Ɠ��������Ƃ�p���Ă悢�B
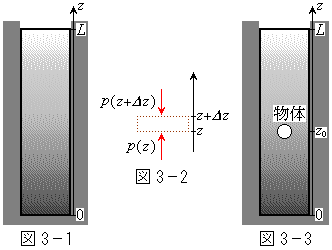 [3]�@�}3�|1�̂悤�ɁA�\���ȍ���L���������A�f�ʐ�S�̉~���e���n�����̋C�̂����Ė����A�C�̂̐�Ή��x�����̒lT�ɕۂB���̂Ƃ��A��l�ȏd�͂̍�p���ł́A�C�̖̂��x�͗e��̒�ɋ߂��قǑ傫���A���x�Ɍ��z�̂����ԂɂȂ�B�e��̒ꂩ�瑪����������z�C�P�ʑ̐ϓ�����̋C�̂̃�������c�Ƃ���Ac��z�̊��Ƃ݂Ȃ����Ƃ��ł��A�W��
[3]�@�}3�|1�̂悤�ɁA�\���ȍ���L���������A�f�ʐ�S�̉~���e���n�����̋C�̂����Ė����A�C�̂̐�Ή��x�����̒lT�ɕۂB���̂Ƃ��A��l�ȏd�͂̍�p���ł́A�C�̖̂��x�͗e��̒�ɋ߂��قǑ傫���A���x�Ɍ��z�̂����ԂɂȂ�B�e��̒ꂩ�瑪����������z�C�P�ʑ̐ϓ�����̋C�̂̃�������c�Ƃ���Ac��z�̊��Ƃ݂Ȃ����Ƃ��ł��A�W��
�@�@�@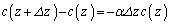 �@�@�@(��)
�@�@�@(��)
���悢�ߎ��łȂ肽�B�����ŁA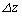 �͍����̍��ł���Aα�͍���z�ɂ��Ȃ����W���ł���B
�͍����̍��ł���Aα�͍���z�ɂ��Ȃ����W���ł���B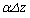 �͏\�����������̂Ƃ���B�܂��A�C��1����������̎��ʂ�m�C�C�̒萔��R�C�d�͉����x�̑傫����g�Ƃ���B
�͏\�����������̂Ƃ���B�܂��A�C��1����������̎��ʂ�m�C�C�̒萔��R�C�d�͉����x�̑傫����g�Ƃ���B
�T�@�e����̋C�̂𗝑z�C�̂Ƃ݂Ȃ��āA�ȉ��̖�ɓ�����B
(1) ����z�ɂ�����C�̂̈��͂�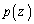 �Ƃ���B
�Ƃ���B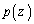 ��
��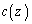 �CT�����R��p���ĕ\���B
�CT�����R��p���ĕ\���B (2) �}3�|2�̂悤�ɁA����z�̈ʒu�ɂ���A����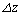 �C�f�ʐ�S�̋C���ɒ��ڂ���B�����ŁA����z�C
�C�f�ʐ�S�̋C���ɒ��ڂ���B�����ŁA����z�C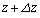 �ɂ�����C�̂̈��͂͂��ꂼ��
�ɂ�����C�̂̈��͂͂��ꂼ��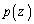 �C
�C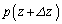 �ł���B�܂��A�C������
�ł���B�܂��A�C������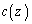 �̕ω��͏\���������A�C�����̋C�̂̃�������
�̕ω��͏\���������A�C�����̋C�̂̃�������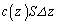 �ŗ^��������̂Ƃ���B���̋C���ɂ͂��炭���������̗͂̂荇����\������^����B
�ŗ^��������̂Ƃ���B���̋C���ɂ͂��炭���������̗͂̂荇����\������^����B (3) ���(1)�C(2)�̌��ʂ���A�W��(��)�̌W��α��m�Cg�CT�����R��p���ĕ\���B
(4) �C�̂̉��x����l��13���̏ꍇ�ɁA�P�ʑ̐ς�����̋C�̂̃�����c��0.10����������悤�ȍ����̍�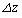 �����߂�B�������A�C��1����������̎��ʂ�
�����߂�B�������A�C��1����������̎��ʂ�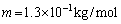 �C�C�̒萔��
�C�C�̒萔��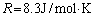 �C�d�͉����x�̑傫����
�C�d�͉����x�̑傫����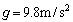 �Ƃ���B
�Ƃ���B (5) �e��̒�Ə�[�ł̒P�ʑ̐ς�����̋C�̂̃������̍�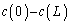 ��m�Cg�CT�CR�Cn�����S��p���ĕ\���B
��m�Cg�CT�CR�Cn�����S��p���ĕ\���B
�U�@�}3�|3�̂悤�ɁA�y���ĕό`���Ȃ������ȕ��̂�e����̋C�̂̒��ɓ���Ă������Ƃ���A�₪�č���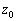 �̈ʒu�ŐÎ~�����B���̂̑̐ς�v�C���ʂ�M�Ƃ��āA�ȉ��̖�ɓ�����B
�̈ʒu�ŐÎ~�����B���̂̑̐ς�v�C���ʂ�M�Ƃ��āA�ȉ��̖�ɓ�����B (1) ����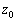 �ɂ�����P�ʑ̐ς�����̋C�̂̃�����
�ɂ�����P�ʑ̐ς�����̋C�̂̃�����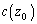 ��M�Cv�����m��p���ĕ\���B
��M�Cv�����m��p���ĕ\���B (2) ���̂�����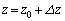 (
(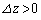 )�ɂ���Ƃ��A���̂ɂ͂��炭��F�̑傫����M�Cg�Cα�C�����
)�ɂ���Ƃ��A���̂ɂ͂��炭��F�̑傫����M�Cg�Cα�C�����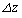 ���g���ĕ\���A�܂��A���̌�������B�������A
���g���ĕ\���A�܂��A���̌�������B�������A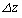 �͏\���������A�W��(��)���Ȃ肽���̂Ƃ��Ă悢�B
�͏\���������A�W��(��)���Ȃ肽���̂Ƃ��Ă悢�B [��]
�e�⌟��
[1](��������)�@���̖��́A���ȏ��������ł��Ă���Ή\�ł��B���ʂȒm����l�����Ȃǂ�m���Ă���K�v�͂���܂���B�ŋ߂̕����̋��ȏ��́A�F����Ő}�\�Ȃǂ��ӂ�ɐ��荞�݁A���������������₷���H�v����Ă��Ă悭�ł��Ă��܂�(�w�K�w���v�̂̍����ɔ����J���L��������̂������ȓ_�͂���܂���)�B���ɁA���Z1�C2�N���́A���ȏ�����������ǂݍ���ł����ׂ��ł��B��b�������}�X�^�[�ł��Ă��Ȃ��̂ɁA�͊w�I�G�l���M�[�ۑ��̓���ȍl����(�����e94�N�O��[1]�Ȃ�)��������Ɏ��g��ł��Ӗ��͂Ȃ��̂ł��B���̖��̏o��҂̈Ӑ}�͂��������Ƃ���ɂ���Ǝv���܂��B
���̖������邽�߂ɕK�v�Ȏ����́A
�n�̃G�l���M�[��D���悤�ȊO�͂��Ȃ���Η͊w�I�G�l���M�[�͕ۑ������Ƃ��������A
�������x�^���̌����F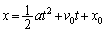 �C
�C
���xv�ƈʒux�̊W�F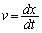
�P�U���̌����F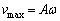 (�܂��́A�ːU��q�̌����F
(�܂��́A�ːU��q�̌����F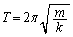 )�C
)�C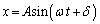
�^���G�l���M�[�F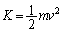
���ꂾ���ł��B����ȍl���������镔���͂���܂���B�{�����[���͂����Ղ肠��̂ŁA�������x�͖���܂����A�m���ʂ�v������Ă���킯�ł͂���܂���B
���啨�������N���ׂĂ̖�肪��b�I�Ȗ�����A�Ƃ����킯�ł͂���܂��A�܂��́A��b�ł߂̂��߂ɂ�������Ƌ��ȏ����悭�ǂ�ł����Ă��������B
[2](��������)�@�l�I�������v�̓d���|�d�������̐}���o�Ă����肷��̂ŁA����R�̂悤�ȓ�₩�A�ƁA�����邩���m��܂���B�ł����A����Ă݂�ƁA��蕶���̃q���g�ɏ]���Čv�Z���Ă䂯�Ή��Ƃ��Ȃ�܂��B�q���g�Ȃ����ƌ��������ł��傤�B�����A�����̖��Ƃ��Ă͌v�Z���ʓ|�Ń{�����[��������̂ŁA�ǂ�ǂ�v�Z��i�߂čs���Ȃ��Ǝ��Ԃ�����Ȃ��Ȃ�܂��B
���̖���'08�N�O��[1]�Ɠ��l�ɁA����ȋZ�I�╨���I�ȍl�@������K�v�͂���܂���B�R���f���T�[�̊�{�����F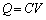 �C
�C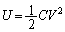 ���x�ŏ[���ɑΉ��ł��܂��B��N�܂łƔ�ׂāA���啨���́A����{�I�ȏo��ɕ����]�������̂ł��傤���H��N��'07�N�O��[3]�����߂������Ƃ̔��Ȃ�����̂����m��܂���B
���x�ŏ[���ɑΉ��ł��܂��B��N�܂łƔ�ׂāA���啨���́A����{�I�ȏo��ɕ����]�������̂ł��傤���H��N��'07�N�O��[3]�����߂������Ƃ̔��Ȃ�����̂����m��܂���B
����ȏݒ�ɘf�킳��Ȃ��悤�ɂ���A���ȏ��̓��e���悭�������A��{�I�Ȗ����K��ς�ł������Ƃɂ��A�����������ɑΏ��ł���͂��ł��B�o��҂̑_�������������Ƃ���ɂ���Ǝv���܂��B���ł���A��������������܂��B�܂��́A��b���K�b�`���ł߂Ă����ė~�����A�Ƃ����A����̃��b�Z�[�W�Ǝ~�߂܂��傤�B
[3](��������)�@���̖�肪�A���Ƃ���3��̒��ł͍ł������g�����ł��B�Ƃ͌����Ă��A�T(1)�`(4)�͊�{���ł��B�U�����̂̉^�����P�U���ł��邱�Ƃ������Ƃ��ɂ悭�o�Ă���`�Ȃ̂ŁA�����Ȗ�肾�Ǝv���܂��B��b���������肵�Ă�����ɂ͉��ł��Ȃ������ł��傤�B
���͇T(5)�ł��B[�ʉ�]�Ɏs�̖{�Ȃǂɏo�Ă�����@�A�K�����̍l�����ɂ��������Ă����܂������A������̎������Ɏv������ł��傤���H�v��������͗��h���Ǝ��͎v���܂����A���̖��̐��������ǂꂭ�炢�Ȃ̂��A����ɕ����Ă݂����Ƃ���ł��B
���́A�����������ł́A���ϕ����g���Ă��܂������Ղ����Ǝv���܂��B
���o����A �C
�C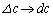 �Ƃ��āA
�Ƃ��āA
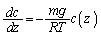 �@����D
�@����D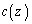 ���o�Ă���̂ŁA���ʂ́A���̎����A�t���̔����@�̌�����p���āA
���o�Ă���̂ŁA���ʂ́A���̎����A�t���̔����@�̌�����p���āA
�Ƃ��Đϕ����A
 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)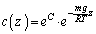 (
( �C
�C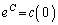 )
)
�ȂǂƂ���Ǝv���܂����A����ł́A
�ƂȂ��Ă��܂��āA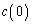 ���c���Ă��܂��܂��B�����Y��Ă������������̂ł��B���́A�����ł͂��߂āA�e����̋C�̗̂ʂ�n�����ł���A�Ƃ��������ɋC�Â��܂����B�K������̘a�̂悤�ȍl�������v�������Ƃ��āA���̏����ɋC�Â���ł��傤���H��蕶�Ƀq���g���~�����C�����܂��B�e����̋C�̗̂ʂ�n�����Ƃ��������́A
���c���Ă��܂��܂��B�����Y��Ă������������̂ł��B���́A�����ł͂��߂āA�e����̋C�̗̂ʂ�n�����ł���A�Ƃ��������ɋC�Â��܂����B�K������̘a�̂悤�ȍl�������v�������Ƃ��āA���̏����ɋC�Â���ł��傤���H��蕶�Ƀq���g���~�����C�����܂��B�e����̋C�̗̂ʂ�n�����Ƃ��������́A
�ƁA�\����܂��B����ŁA�D�̌`�̂܂܁AS��������z�Őϕ�����悢���낤�A�Ƃ������ƂɂȂ�܂��B
�������A�K������̘a�̂悤�ɍl���Ă��āA�e���z������N�ɕ����āA
�Ƃ���Γ������Ƃł����A'08�O��[2]�ɐe�ȗU�������Ă���̂Ɣ�ׂ�ƁA���̖��́A������Ɩ����ȋC�����܂��B�����A�قƂ�ǂ̎��͂������p�X���ćU�ɐi��ł��܂��Ă���Ǝv���̂ŁA�����I�Ȕ�Q�������͂قƂ�ǂ��Ȃ������Ǝv���܂�����ǂ��B����ƁA���́A�K������̂悤�ȍl������S���v���������܂���ł����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���啨��TOP�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B