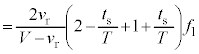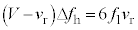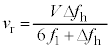東大物理'24年前期[3]
音波に関する以下の設問に答えよ。空気中の音速をVとし、風の影響は無視せよ。
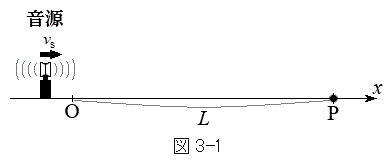 Ⅰ x軸正負の方向に音波を発生する音源が、一定の速さ
Ⅰ x軸正負の方向に音波を発生する音源が、一定の速さ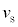 (
(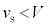 )でx軸上を正の向きに運動している。音源の振動数は
)でx軸上を正の向きに運動している。音源の振動数は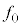 で一定である。時刻
で一定である。時刻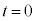 に音源は
に音源は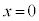 の原点Oを通過した。音源の大きさは無視できる。
の原点Oを通過した。音源の大きさは無視できる。図3-1のように、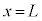 の点をPとする。ただし、
の点をPとする。ただし、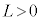 とする。時刻
とする。時刻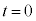 に音源で発生した音波が点Pに到達する時刻を
に音源で発生した音波が点Pに到達する時刻を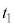 とする。
とする。
(1) 時刻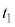 に音源で発生した音波が点Pに到達する時刻を
に音源で発生した音波が点Pに到達する時刻を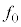 ,
,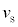 ,V,Lのうち必要なものを用いて表せ。
,V,Lのうち必要なものを用いて表せ。
(2) 点Pでの音波の位相が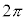 だけ変化するために要する時間を
だけ変化するために要する時間を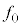 ,
,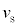 ,V,Lのうち必要なものを用いて表せ。
,V,Lのうち必要なものを用いて表せ。 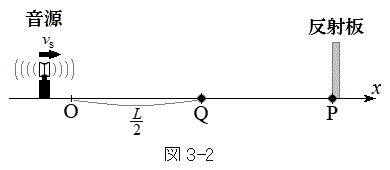 続いて、図3-2のように、反射板を点Pに置く。音源から直接届く音波と反射板で反射されて届く音波の干渉によりうなりが生じる。
続いて、図3-2のように、反射板を点Pに置く。音源から直接届く音波と反射板で反射されて届く音波の干渉によりうなりが生じる。
(3) 観測者が音源とともに運動する場合を考える。観測者と音源の距離は小さく、観測者は音源と同じ位置にいるとしてよい。音源が反射板に到達するまでの間に観測されるうなりの振動数(うなりの周期の逆数)を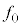 ,
,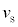 ,V,Lのうち必要なものを用いて表せ。
,V,Lのうち必要なものを用いて表せ。
(4) 観測者が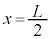 の点Qに静止している場合を考える。ある時刻にうなりが観測され始めた。うなりが観測され始める時刻と、観測されるうなりの振動数をそれぞれ
の点Qに静止している場合を考える。ある時刻にうなりが観測され始めた。うなりが観測され始める時刻と、観測されるうなりの振動数をそれぞれ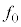 ,
, ,V,Lのうち必要なものを用いて表せ。ただし、音源が原点Oを通過するとき、反射板で反射された音波は原点Oに到達しているものとする。また、音源の運動は観測者に影響されることはなく、音波は音源や観測者に遮られない。
,V,Lのうち必要なものを用いて表せ。ただし、音源が原点Oを通過するとき、反射板で反射された音波は原点Oに到達しているものとする。また、音源の運動は観測者に影響されることはなく、音波は音源や観測者に遮られない。
Ⅱ 音源から出る音波の振動数が時刻t によって変化する場合を考える。音源は原点Oに静止している。反射板はx軸上を運動できる。音源の大きさは無視できる。
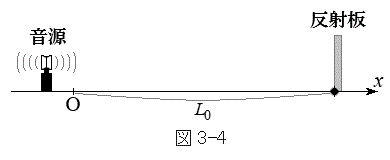 (1) 振動数が図3-3(A)のように時間変化する音波を音源から発生させる。図3-4のように反射板は位置
(1) 振動数が図3-3(A)のように時間変化する音波を音源から発生させる。図3-4のように反射板は位置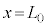 に静止している。ただし、
に静止している。ただし、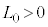 である。このとき、うなりの振動数は
である。このとき、うなりの振動数は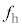 であった。
であった。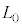 を
を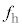 ,
,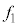 ,T,Vのうち必要なものを用いて表せ。
,T,Vのうち必要なものを用いて表せ。
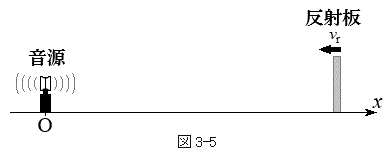 次に、図3-5のように反射板が音源に向って一定の速さ
次に、図3-5のように反射板が音源に向って一定の速さ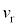 で近づく場合を考える。ただし、時刻
で近づく場合を考える。ただし、時刻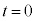 での反射板の位置を
での反射板の位置を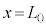 とし、
とし、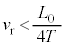 とする。
とする。
(2) 振動数が図3-3(A)のように時間変化する音波を音源から発生させる。時刻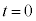 に音源で発生した音波は、ある位置
に音源で発生した音波は、ある位置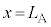 で反射板により反射され、時刻
で反射板により反射され、時刻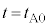 に原点Oに到達した。
に原点Oに到達した。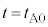 に観測されるうなりの振動数を
に観測されるうなりの振動数を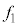 ,T,
,T,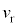 ,V,
,V,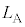 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(3) 振動数が図3-3(B)のように時間変化する音波を音源から同時に発生させる。時刻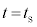 に音源で発生した音波は、ある位置
に音源で発生した音波は、ある位置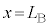 で反射板により反射され、時刻
で反射板により反射され、時刻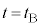 に原点Oに到達した。ただし、
に原点Oに到達した。ただし、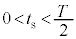 とする。時刻
とする。時刻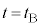 に観測されるうなりの振動数を
に観測されるうなりの振動数を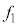 ,
,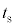 ,T,
,T,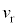 ,V,
,V,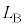 のうち必要なものを用いて表せ。
のうち必要なものを用いて表せ。
(4) 振動数が図3-3(A)と図3-3(B)のように時間変化する音波を音源から同時に発生させる。振動数が図3-3(A)のように時間変化する音波とその反射波によるうなりの振動数を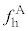 ,振動数が図3-3(B)のように時間変化する音波とその反射波によるうなりの振動数を
,振動数が図3-3(B)のように時間変化する音波とその反射波によるうなりの振動数を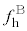 とする。うなりの振動数の差
とする。うなりの振動数の差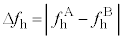 を
を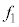 ,T,
,T,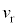 ,Vのうち必要なものを用いて表せ。
,Vのうち必要なものを用いて表せ。
(5) 設問Ⅱ(4)における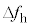 の測定により
の測定により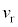 を求めることができる。
を求めることができる。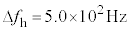 ,
,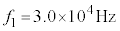 ,
,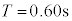 ,
,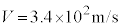 として、
として、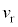 を有効数字2桁で求めよ。
を有効数字2桁で求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 ドップラー効果によるうなりの振動数の測定により、運動する物体の位置、速度を求める、という問題です。Ⅱ(3)でうなりを起こす2つの振動数のどちらが大きいのかが問題になるのですが、(5)の問題文の数値と(1)の結果から判断するしかありません。
(1) 時間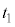 の間に音源は
の間に音源は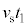 進んでいるので、音波が進む距離は
進んでいるので、音波が進む距離は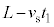 ,この距離を音波が進む時間
,この距離を音波が進む時間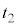 は、
は、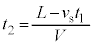 ・・・②
・・・② よって、音波が点Pに到達する時刻は、①より、
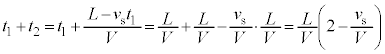 ......[答]
......[答]
(2) 点Pで位相が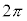 だけ変化する時間は、音波の周期です。音波の波長をλとして、点Pに音波が到着したのと同時に、点Pから波長λだけ離れた位置から発せられた音波が点Pに到着する時間です。よって、①,②のL→λとして、その時間
だけ変化する時間は、音波の周期です。音波の波長をλとして、点Pに音波が到着したのと同時に、点Pから波長λだけ離れた位置から発せられた音波が点Pに到着する時間です。よって、①,②のL→λとして、その時間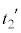 は、
は、 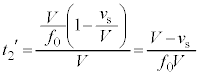 ......[答]
......[答]注.本問は、ドップラー効果の公式を覚えていなくても解答できるように配慮されているので上記では②を用いましたが、②によらず、ドップラー効果の公式を用いて、点Pで聞く音波の振動数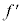 は、
は、 求める時間はこの逆数で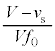 ,として解答できます。以後は、ドップラー効果の公式を用いて解答します。
,として解答できます。以後は、ドップラー効果の公式を用いて解答します。
(3) 反射板で聞く音波の振動数は、ドップラー効果の公式より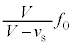 です。反射音を聞く観測者は、速さ
です。反射音を聞く観測者は、速さ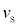 で反射音の音源である反射板に近づくので、観測者が聞く振動数
で反射音の音源である反射板に近づくので、観測者が聞く振動数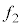 は、ドップラー効果の公式より、
は、ドップラー効果の公式より、 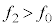 に注意して、うなりの振動数は、
に注意して、うなりの振動数は、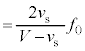 ......[答]
......[答]
(4) 音源が点Qに到達するまでは、点Qにいる観測者が聞く振動数は、直接音、反射音ともに、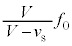 なので、うなりは生じません。うなりが観測され始めるのは、音源が点Qを通過したときで、その時刻は
なので、うなりは生じません。うなりが観測され始めるのは、音源が点Qを通過したときで、その時刻は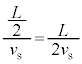 ......[答]
......[答] 音源が点Qを通過すると、点Qで聞く反射音の振動数は変わらず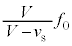 ですが、点Qで聞く直接音の振動数は
ですが、点Qで聞く直接音の振動数は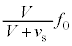 となります。点Qで観測されるうなりの振動数は、
となります。点Qで観測されるうなりの振動数は、 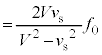 ......[答]
......[答]
Ⅱ(1) 音源を出た音波が反射板との間を往復する時間は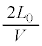 です。反射音が音源を出た時刻を
です。反射音が音源を出た時刻を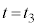 として、反射板は静止しているので、観測者が聞く反射音の振動数は
として、反射板は静止しているので、観測者が聞く反射音の振動数は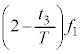 ,直接音の振動数は
,直接音の振動数は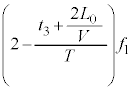 です(
です(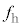 )。うなりの振動数が
)。うなりの振動数が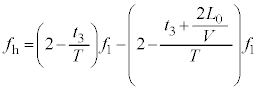 だったので、
だったので、 ∴ 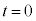 ......[答]
......[答]
(2) 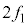 に音源を出た音波の振動数は
に音源を出た音波の振動数は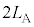 です。問題文より
です。問題文より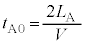 にいる反射板で反射されるので、この音波は距離
にいる反射板で反射されるので、この音波は距離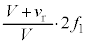 を往復して原点Oにいる音源に戻ってきます。その時間は、
を往復して原点Oにいる音源に戻ってきます。その時間は、 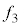 ・・・③
・・・③ドップラー効果の公式より、この音波を反射板が聞く振動数は、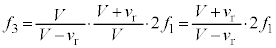 ,音源のすぐ近くにいる観測者が聞く反射音の振動数
,音源のすぐ近くにいる観測者が聞く反射音の振動数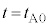 は、
は、 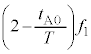 ・・・④
・・・④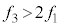 に音源が発生する音波の振動数は
に音源が発生する音波の振動数は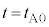 です。観測者は反射音とともにこの振動数の音波を聞きます。
です。観測者は反射音とともにこの振動数の音波を聞きます。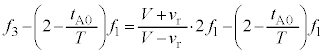 に注意して、
に注意して、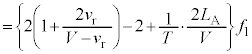 に観測されるうなりの振動数は、④より、
に観測されるうなりの振動数は、④より、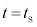 (∵ ③)
(∵ ③)
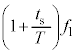 ......[答]
......[答]
(3) 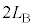 に音源を出た音波の振動数は
に音源を出た音波の振動数は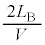 です。この音波が距離
です。この音波が距離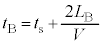 を往復して原点に戻ってくるまでの時間は
を往復して原点に戻ってくるまでの時間は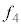 です。よって、
です。よって、 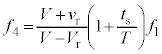 ・・・⑤
・・・⑤(2)と同様にドップラー効果の公式を用いると、この音波が反射板で反射して、音源のすぐ近くにいる観測者が聞く反射音の振動数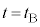 は、
は、 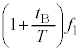 ・・・⑥
・・・⑥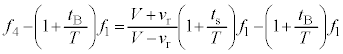 に音源が発生する音波の振動数は
に音源が発生する音波の振動数は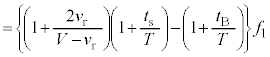 です。両振動数の差をとると、⑥より、
です。両振動数の差をとると、⑥より、下記注より、これは負なので、うなりの振動数は、
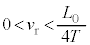 ......[答]
......[答]注.上記中カッコ内の正負を調べます。音波が反射板に到達するまでの時間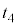 は、
は、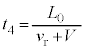 です。
です。 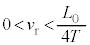 なので、
なので、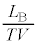 は、
は、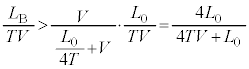 ・・・⑦
・・・⑦一方で、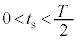 より、
より、 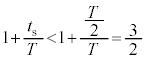 ・・・⑧
・・・⑧(1)の結果より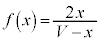 ですが、
ですが、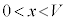 なので、
なので、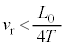 ・・・⑨
・・・⑨
つまり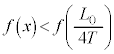 ,
,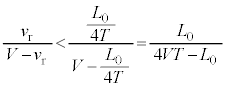 です。関数
です。関数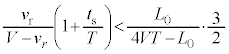 は、
は、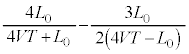 において単調増加なので、
において単調増加なので、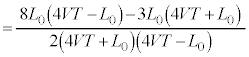 より
より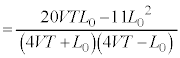 です。よって、
です。よって、 ⑧と合わせて、
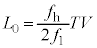 ・・・⑩
・・・⑩⑦の右辺-⑩の右辺より、
⑨より、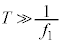 と考えられます。つまり、
と考えられます。つまり、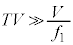 であって、
であって、 つまり、(3)のうなりの振動数の結果は正です。
ただ試験会場でこんな確認作業をやっている余裕はありません。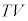 という条件は、音速Vをかけると、
という条件は、音速Vをかけると、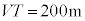 となり、
となり、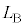 は音波の波長で、距離
は音波の波長で、距離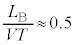 が音波の波長(1cm~30m程度)よりも充分に大きい、ということを言っています。(5)で与えられる数値によると
が音波の波長(1cm~30m程度)よりも充分に大きい、ということを言っています。(5)で与えられる数値によると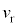 程度で、
程度で、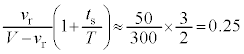 が100m程度として
が100m程度として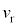 ,ここで
,ここで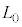 を大きめに見積もって50m/s程度(自転車程度)として
を大きめに見積もって50m/s程度(自転車程度)として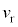 であれば、つまり、問題文が想定している程度の状況では、反射音よりも音源から直接来る音波の方が振動数が大きい、と考えることができます。ただ、
であれば、つまり、問題文が想定している程度の状況では、反射音よりも音源から直接来る音波の方が振動数が大きい、と考えることができます。ただ、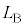 が250m/s,
が250m/s,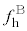 が1000m程度になる(ミサイルを迎撃する、というような状況)と、
が1000m程度になる(ミサイルを迎撃する、というような状況)と、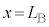 が大きく
が大きく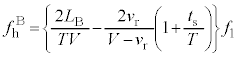 が小さくなり、反射音の方が振動数が大きくなることもあり得て、状況は微妙になります。(4)の
が小さくなり、反射音の方が振動数が大きくなることもあり得て、状況は微妙になります。(4)の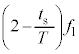 はどちらの振動数の方が大きいのか判断しないといけませんが、(3)だけなら絶対値をつけて解答する方がよいと思います。
はどちらの振動数の方が大きいのか判断しないといけませんが、(3)だけなら絶対値をつけて解答する方がよいと思います。
(4) (3)と同様に反射板が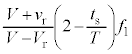 に来ているとして、(3)より、
に来ているとして、(3)より、 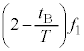 ・・・⑪
・・・⑪また、図3-3(A)のように振動数が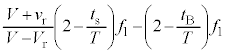 と時間変化する音波の場合も、(3)と同様に考えて、反射音を聞く振動数
と時間変化する音波の場合も、(3)と同様に考えて、反射音を聞く振動数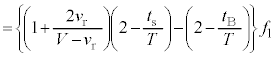 と直接音を聞く振動数
と直接音を聞く振動数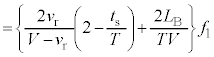 との差は、
との差は、 中カッコ内は正なので、
⑪より、
(5) (5)の結果より、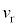
数値代入して、
よって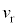 は、有効数字2桁で、
は、有効数字2桁で、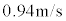 ......[答] (これは歩く速さ程度です)
......[答] (これは歩く速さ程度です)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大物理TOP 物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 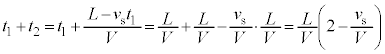 ......[答]
......[答]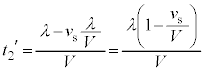
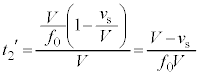 ......[答]
......[答]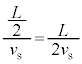 ......[答]
......[答]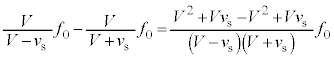
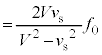 ......[答]
......[答]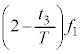 ,直接音の振動数は
,直接音の振動数は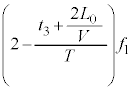 です(
です(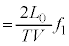
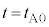 です。観測者は反射音とともにこの振動数の音波を聞きます。
です。観測者は反射音とともにこの振動数の音波を聞きます。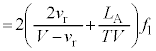
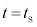 (∵ ③)
(∵ ③)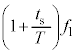 ......[答]
......[答]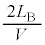 です。この音波が距離
です。この音波が距離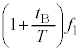 ・・・⑥
・・・⑥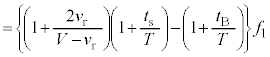 です。両振動数の差をとると、⑥より、
です。両振動数の差をとると、⑥より、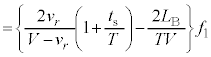
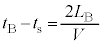
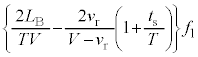
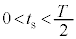 (∵ ⑤)
(∵ ⑤)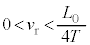 ......[答]
......[答]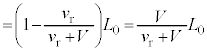
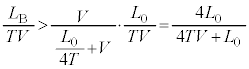 ・・・⑦
・・・⑦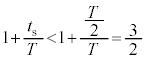 ・・・⑧
・・・⑧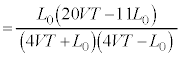
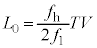 ・・・⑩
・・・⑩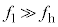
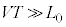
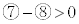
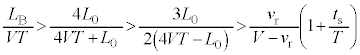
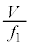
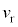 であれば、つまり、問題文が想定している程度の状況では、反射音よりも音源から直接来る音波の方が振動数が大きい、と考えることができます。ただ、
であれば、つまり、問題文が想定している程度の状況では、反射音よりも音源から直接来る音波の方が振動数が大きい、と考えることができます。ただ、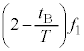 ・・・⑪
・・・⑪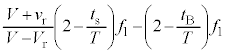 と時間変化する音波の場合も、(3)と同様に考えて、反射音を聞く振動数
と時間変化する音波の場合も、(3)と同様に考えて、反射音を聞く振動数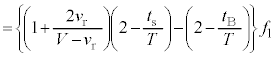 と直接音を聞く振動数
と直接音を聞く振動数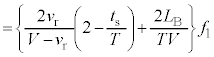 との差は、
との差は、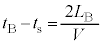
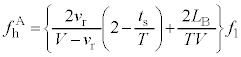
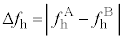
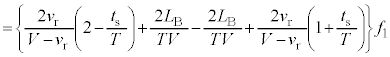 (∵ ⑤)
(∵ ⑤)