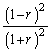力学(分裂・衝突)演習問題
筑波大物理'08年[1]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
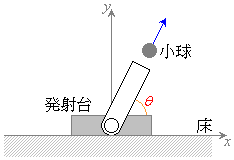 図のように水平な床に置かれた発射台を考える。この発射台は、一定のエネルギー
図のように水平な床に置かれた発射台を考える。この発射台は、一定のエネルギー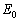 を瞬時に小球と発射台の運動エネルギーに変換することで小球を発射できる。この小球は大きさが無視でき、質量mをもつ。小球を含まない発射台の質量をMとする。床と発射台の間には摩擦がなく、発射台は床の上の直線上を自由に動くことができる。この直線をx軸とし、x軸に垂直で鉛直上向きをy軸とする。この小球の発射方向はx-y面内で動かすことができ、発射方向とx軸正方向のなす角θ は
を瞬時に小球と発射台の運動エネルギーに変換することで小球を発射できる。この小球は大きさが無視でき、質量mをもつ。小球を含まない発射台の質量をMとする。床と発射台の間には摩擦がなく、発射台は床の上の直線上を自由に動くことができる。この直線をx軸とし、x軸に垂直で鉛直上向きをy軸とする。この小球の発射方向はx-y面内で動かすことができ、発射方向とx軸正方向のなす角θ は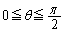 の範囲で調整することができる。小球は床の高さから発射されるとしてよい。重力加速度は鉛直下向きでその大きさをgとする。また、空気抵抗、小球発射前後での
の範囲で調整することができる。小球は床の高さから発射されるとしてよい。重力加速度は鉛直下向きでその大きさをgとする。また、空気抵抗、小球発射前後での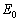 にかかわる質量変化はないものとする。
にかかわる質量変化はないものとする。
以下、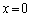 の位置で静止している発射台から小球を発射する場合を考える。
の位置で静止している発射台から小球を発射する場合を考える。
問1 小球発射直後の小球と発射台の速度をそれぞれ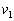 ,
,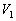 とするとき、小球発射前後でのエネルギー保存、水平方向の運動量保存を表す式を示せ。
とするとき、小球発射前後でのエネルギー保存、水平方向の運動量保存を表す式を示せ。 問2 発車直後の小球の速度の水平(x)成分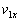 ,垂直(y)成分
,垂直(y)成分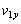 をm,M,
をm,M,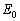 ,θ を用いて表せ。
,θ を用いて表せ。 問3 発射直後の小球の発射台に対する相対速度の大きさをm,M,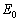 ,θ を用いて表せ。
,θ を用いて表せ。 問4 発射された小球が床に最初に落ちる位置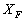 をg,m,M,
をg,m,M,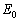 ,θ を用いて表せ。
,θ を用いて表せ。 問5 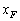 を最大にするための角度θ は
を最大にするための角度θ は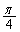 より大きいか小さいかを理由とともに示せ。
より大きいか小さいかを理由とともに示せ。 [解答へ]
上智大理工物理'09年[1]
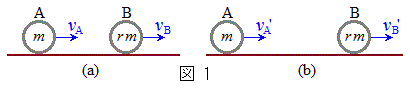 摩擦がなく左右に無限に広がっている床の上に、図1のように一直線上に物体A,Bがある。物体Aと物体Bの質量はそれぞれmとそのr倍、
摩擦がなく左右に無限に広がっている床の上に、図1のように一直線上に物体A,Bがある。物体Aと物体Bの質量はそれぞれmとそのr倍、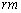 である。
である。
 次に、図2のように物体A,Bの右側に質量がmの物体Cを置き、物体BとCを静止させた状態で、一番左の物体Aに右向きに速度v (
次に、図2のように物体A,Bの右側に質量がmの物体Cを置き、物体BとCを静止させた状態で、一番左の物体Aに右向きに速度v (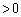 )を与えた。物体同士の衝突は弾性衝突とする。
)を与えた。物体同士の衝突は弾性衝突とする。
2.AがBに衝突したあとのAとBの速度はそれぞれ、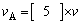 ,
,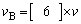 である。この衝突の後、Aは右向きに進んだ。これより、
である。この衝突の後、Aは右向きに進んだ。これより、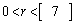 であることがわかる。
であることがわかる。 3.次に、BはCに衝突する。この衝突後のCの速度は、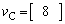 である。また、衝突後のBの速度は
である。また、衝突後のBの速度は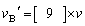 なので、Bは左向きに進むことがわかる。
なので、Bは左向きに進むことがわかる。 4.3.の衝突後、左向きに進むBは、右向きに進んでいるAと衝突する。この衝突の結果、Aは静止し、Bは右向きに進んだ。Aが静止したことにより、質量がmと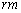 の2個の物体(物体Cと物体B)が動いている状態となる。したがって、Cの速度はこの衝突直前のAの速度
の2個の物体(物体Cと物体B)が動いている状態となる。したがって、Cの速度はこの衝突直前のAの速度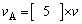 と等しいはずである。よって、
と等しいはずである。よって、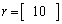 であることがわかる。また、右向きに進むBの速度も2.での衝突後のBの速度
であることがわかる。また、右向きに進むBの速度も2.での衝突後のBの速度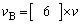 に等しい。
に等しい。 5.Bの方が速いので、BとCは再び衝突する。衝突後の速度は、それぞれ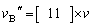 ,
,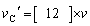 となる。
となる。
[ 1 ]〜[ 6 ],[ 8 ],[ 9 ],[ 11 ],[ 12 ]の選択肢
a) 0 b) 1 c) 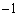 d)
d) 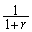 e)
e) 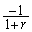 f)
f) 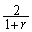 g)
g) 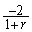 h)
h) 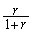 i)
i) 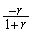 j)
j) 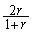 k)
k) 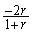 l)
l) 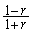 m)
m) 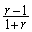 n)
n) 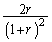 o)
o) 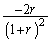 p)
p) 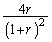 q)
q) 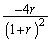 r)
r) 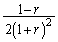 s)
s) 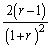 t)
t) 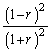
[ 7 ],[ 10 ]の選択肢
a) 0 b) 1 c) 2 d) 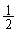 e)
e) 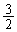 f)
f) 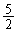 g)
g) 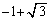 h)
h) 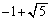 i)
i) 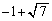 j)
j) 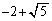 k)
k) 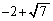 l)
l) 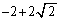
[解答へ]
名工大物理'09年[1]
粗い平板の上を転がることなくすべる小さな物体の運動に関する以下の問いに答えよ。ただし、重力加速度の大きさを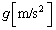 とする。物体の大きさは考えなくてよい。また、必要であれば以下の関係を用いよ。
とする。物体の大きさは考えなくてよい。また、必要であれば以下の関係を用いよ。
「初項が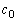 で公比r (
で公比r (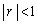 )の無限等比級数の和は
)の無限等比級数の和は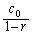 で表せる。」
で表せる。」 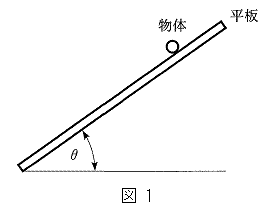 問1 次の文中の(ア)〜(ウ)の空欄に適切な式を入れよ。
問1 次の文中の(ア)〜(ウ)の空欄に適切な式を入れよ。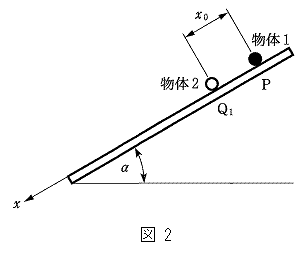 問2 図2に示すように粗い平板を水平から測った傾斜角が
問2 図2に示すように粗い平板を水平から測った傾斜角が となるよう固定した(
となるよう固定した(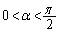 )。平板に沿ってx軸をとり、図中の矢の向きを正とする。質量が
)。平板に沿ってx軸をとり、図中の矢の向きを正とする。質量が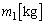 の物体1を点Pに、質量が
の物体1を点Pに、質量が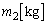 の物体2を点Pからx軸の正の向きに
の物体2を点Pからx軸の正の向きに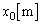 だけ離れた点
だけ離れた点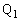 において静かに離した。物体2は静止したままであったが、物体1はその直後にすべり始め、物体2に衝突した。物体1と物体2の反発係数(はねかえり係数)はe (
において静かに離した。物体2は静止したままであったが、物体1はその直後にすべり始め、物体2に衝突した。物体1と物体2の反発係数(はねかえり係数)はe (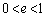 )である。衝突は瞬時に起こるものとする。また、平板と物体1の動摩擦係数は
)である。衝突は瞬時に起こるものとする。また、平板と物体1の動摩擦係数は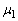 ,平板と物体2の動摩擦係数は
,平板と物体2の動摩擦係数は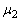 である。
である。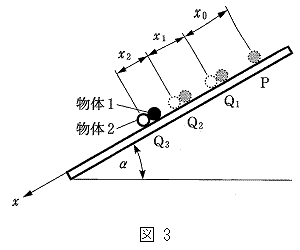 (2) 点
(2) 点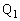 での衝突後、物体1は再度すべり始め、図3に示すように点
での衝突後、物体1は再度すべり始め、図3に示すように点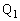 からx方向に
からx方向に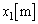 だけ離れた点
だけ離れた点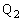 において物体2と再衝突した。この再衝突の直前に物体2の速度はちょうど0となった。このとき、
において物体2と再衝突した。この再衝突の直前に物体2の速度はちょうど0となった。このとき、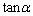 を
を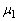 と
と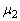 を用いて表せ。また、
を用いて表せ。また、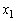 を求めよ。
を求めよ。(3) 点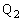 での衝突直後の物体1,2の速度
での衝突直後の物体1,2の速度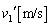 ,
,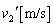 を求めよ。
を求めよ。 (4) 点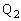 での衝突後、物体1は再度すべり始め、図3に示すように点
での衝突後、物体1は再度すべり始め、図3に示すように点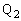 からx方向に
からx方向に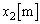 だけ離れた点
だけ離れた点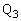 において物体2と再衝突した。この点
において物体2と再衝突した。この点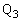 における衝突直後の物体2の速度
における衝突直後の物体2の速度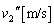 を求めよ。また、
を求めよ。また、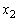 を求めよ。
を求めよ。 (5) このように、物体1,2は衝突を繰り返しながら斜面をすべり、やがて両物体とともに斜面上で静止した。物体1が点Pから静止するまでにすべった距離を求めよ。
[解答へ]
早大理工物理'09年[3]
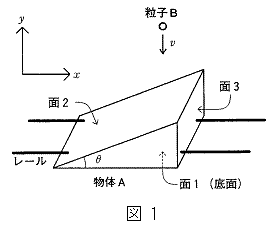 空間に固定された無限に長い2本のレールがある。レールはx軸に平行である。このレールにそって運動する質量Mの物体Aを考える(図1)。物体Aは5つのなめらかな面をもつ。面1は2辺がレールに平行な長方形で、かつ、y軸に垂直である。面2は面1とのなす角がθ の斜面である。面3はx軸に垂直である。残りの2つの面はそれぞれ面1に垂直である。
空間に固定された無限に長い2本のレールがある。レールはx軸に平行である。このレールにそって運動する質量Mの物体Aを考える(図1)。物体Aは5つのなめらかな面をもつ。面1は2辺がレールに平行な長方形で、かつ、y軸に垂直である。面2は面1とのなす角がθ の斜面である。面3はx軸に垂直である。残りの2つの面はそれぞれ面1に垂直である。
y軸の負の方向に一定の速さvで運動する質量mの粒子Bが物体Aに衝突する。衝突は弾性衝突とする。粒子Bと物体Aとの間の摩擦、および重力は無視する。このとき、以下の問いに答えよ。
まず、物体Aがレールに固定された状況を考える。
問1 粒子Bが物体Aの面2に衝突するとき、粒子Bは面2に垂直な力積を受ける。力積の大きさをPとし、粒子Bの衝突後の速度のx成分とy成分をそれぞれ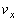 ,
,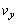 として、
として、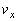 とPの関係式、および
とPの関係式、および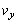 とPの関係式をそれぞれ書け。
とPの関係式をそれぞれ書け。 問2 衝突の前後で粒子Bの運動エネルギーが保存されることを用いて、Pを求めよ。答はv,m,θ のうち適当なものを用いて表せ。
つぎに、物体Aがレールにそって自由に動ける状況を考える。レールと物体Aとの間の摩擦は無視する。
問3 速さVでx軸の正の方向に動いている物体Aの面2に粒子Bが衝突するとき、問1と同様に、粒子Bは面2に垂直な力積を受ける。このとき、粒子Bが受ける力積の大きさ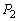 を求めよ。答はv,V,m,M,θ のうち適当なものを用いて表せ。
を求めよ。答はv,V,m,M,θ のうち適当なものを用いて表せ。 問4 速さVでx軸の正の方向に動いている物体Aの面3に粒子Bが衝突するとき、粒子Bは面3に垂直な力積を受ける。この力積の大きさ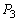 を求めよ。答はv,V,m,M,θ のうち適当なものを用いて表せ。
を求めよ。答はv,V,m,M,θ のうち適当なものを用いて表せ。 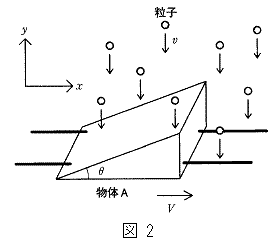 さらに、粒子Bと同じ粒子が空間に一様に分布しており、それぞれがy軸の負の方向に一定の速さvで運動し、物体Aと衝突する状況を考える(図2)。単位体積あたりの粒子数をnとする。物体Aの質量Mが粒子の質量mよりも十分に大きく、さらにnが十分に大きいとき、多数の粒子の衝突によって生じる平均の力により、物体Aはなめらかに運動する。このときの物体Aの運動について考える。粒子と物体Aとの衝突はすべて弾性衝突とする。レールと物体Aとの間の摩擦、粒子と物体Aとの間の摩擦、および重力は無視する。また、粒子同士の衝突、および粒子とレールとの衝突も無視する。このとき、以下の問いに答えよ。
さらに、粒子Bと同じ粒子が空間に一様に分布しており、それぞれがy軸の負の方向に一定の速さvで運動し、物体Aと衝突する状況を考える(図2)。単位体積あたりの粒子数をnとする。物体Aの質量Mが粒子の質量mよりも十分に大きく、さらにnが十分に大きいとき、多数の粒子の衝突によって生じる平均の力により、物体Aはなめらかに運動する。このときの物体Aの運動について考える。粒子と物体Aとの衝突はすべて弾性衝突とする。レールと物体Aとの間の摩擦、粒子と物体Aとの間の摩擦、および重力は無視する。また、粒子同士の衝突、および粒子とレールとの衝突も無視する。このとき、以下の問いに答えよ。
問5 物体Aがx軸の正の方向に速さVで動いているとき、時間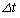 の間に粒子が物体Aの面2に及ぼす平均の力のx成分を
の間に粒子が物体Aの面2に及ぼす平均の力のx成分を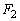 ,面3に及ぼす平均の力を
,面3に及ぼす平均の力を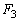 とする。物体Aの質量は粒子の質量よりも十分に大きく(
とする。物体Aの質量は粒子の質量よりも十分に大きく(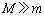 )、さらに時間
)、さらに時間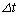 は十分に短いため、
は十分に短いため、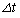 間の物体Aの速さは一定とみなせる。
間の物体Aの速さは一定とみなせる。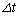 の間に物体Aの面2、および面3に衝突する粒子の数をそれぞれ
の間に物体Aの面2、および面3に衝突する粒子の数をそれぞれ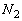 ,
,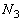 として、
として、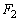 ,
,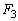 をそれぞれ求めよ。答はm,v,V,
をそれぞれ求めよ。答はm,v,V,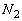 ,
,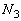 ,
,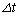 ,θ のうち適当なものを用いて表せ。
,θ のうち適当なものを用いて表せ。 問6 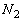 ,
,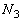 をそれぞれ求めよ。ただし、面2の体積をSとする。答はv,V,n,
をそれぞれ求めよ。ただし、面2の体積をSとする。答はv,V,n,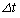 ,θ,Sのうち適当なものを用いて表せ。
,θ,Sのうち適当なものを用いて表せ。 問7 十分に時間がたつと、物体Aは初速度によらずにx軸の正の方向に等速度運動をするようになる。物体Aの質量は粒子の質量よりも十分に大きいとして(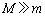 )、このときの物体Aの速さを求めよ。答はvとθ を用いて表せ。
)、このときの物体Aの速さを求めよ。答はvとθ を用いて表せ。 [解答へ]
名大物理'10年[1]
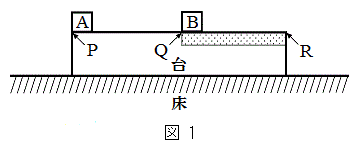 図1のように、水平な床の上に質量
図1のように、水平な床の上に質量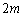 の水平な台を置き、大きさが無視できる2つの小物体A,Bの台の上面での運動を考える。紙面に垂直な方向の運動は考えない。小物体A,Bの質量はともにmとする。台の上面のうちPQ間はなめらかであり、この区間では台と小物体A,Bとの間の摩擦は無視できる。QR間には摩擦があり、小物体A,Bと台の上面QR間との間の静止摩擦係数はμ,動摩擦係数は
の水平な台を置き、大きさが無視できる2つの小物体A,Bの台の上面での運動を考える。紙面に垂直な方向の運動は考えない。小物体A,Bの質量はともにmとする。台の上面のうちPQ間はなめらかであり、この区間では台と小物体A,Bとの間の摩擦は無視できる。QR間には摩擦があり、小物体A,Bと台の上面QR間との間の静止摩擦係数はμ,動摩擦係数は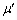 である。また、小物体Aと小物体Bの衝突における反発係数(はねかえり係数)eは
である。また、小物体Aと小物体Bの衝突における反発係数(はねかえり係数)eは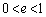 を満たす。重力加速度をgとして、以下の問いに答えよ。
を満たす。重力加速度をgとして、以下の問いに答えよ。
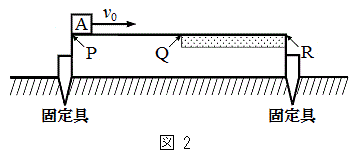 はじめに、台を床に固定具で固定し、小物体Bを台上から取り除く。台上での小物体Aの運動を考える。図2のように、小物体Aを台の上面のP点から初速度
はじめに、台を床に固定具で固定し、小物体Bを台上から取り除く。台上での小物体Aの運動を考える。図2のように、小物体Aを台の上面のP点から初速度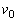 で右向きに滑らせたところ、小物体AはQ点から距離
で右向きに滑らせたところ、小物体AはQ点から距離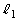 だけ離れた台上の点で静止した。
だけ離れた台上の点で静止した。
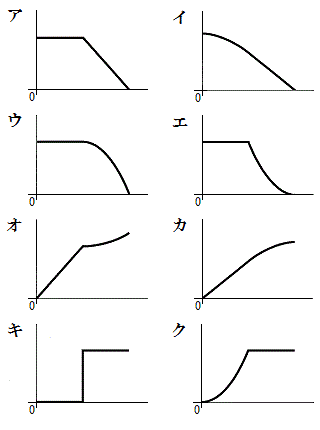 設問(1):運動をはじめてから静止するまでの小物体Aの運動を考える。(a)小物体Aの速度の時間変化、(b)運動エネルギーの時間変化、(c)P点から小物体Aまでの距離の時間変化を示すグラフとして適切なものを次のア〜クからそれぞれ一つずつ選べ。ただし、グラフの横軸は小物体Aが運動を開始してからの時間を表し、縦軸は速度、運動エネルギー、または距離を表すものとする。
設問(1):運動をはじめてから静止するまでの小物体Aの運動を考える。(a)小物体Aの速度の時間変化、(b)運動エネルギーの時間変化、(c)P点から小物体Aまでの距離の時間変化を示すグラフとして適切なものを次のア〜クからそれぞれ一つずつ選べ。ただし、グラフの横軸は小物体Aが運動を開始してからの時間を表し、縦軸は速度、運動エネルギー、または距離を表すものとする。
設問(2):距離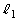 を、m,μ,
を、m,μ,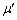 ,e,g,
,e,g,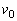 の中から適切なものを用いて表せ。
の中から適切なものを用いて表せ。
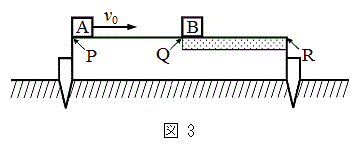 次に、台を床に固定具で固定したまま、小物体Bを台上のQ点に静かに置く。図3のように台の上面のP点から、初速度
次に、台を床に固定具で固定したまま、小物体Bを台上のQ点に静かに置く。図3のように台の上面のP点から、初速度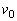 で小物体Aを右向きに滑らせると、小物体Aと小物体Bは衝突を起こし、衝突後、Q点からそれぞれ右に距離
で小物体Aを右向きに滑らせると、小物体Aと小物体Bは衝突を起こし、衝突後、Q点からそれぞれ右に距離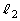 ,
,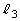 だけ離れた台上の点に静止した。
だけ離れた台上の点に静止した。
設問(3):衝突直後の小物体Aと小物体Bの運動エネルギーを、m,μ,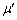 ,e,g,
,e,g,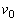 の中から適切なものを用いてそれぞれ表せ。
の中から適切なものを用いてそれぞれ表せ。
設問(4):距離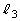 と距離
と距離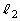 との差
との差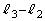 を、m,μ,
を、m,μ,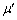 ,e,g,
,e,g,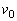 の中から適切なものを用いて表せ。
の中から適切なものを用いて表せ。
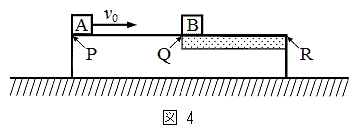 次に、台を床に固定する固定具を取り外し、台が床の上を自由に滑ることができるようにする。床と台との間の摩擦は無視できる。静止した台の上のQ点に小物体Bを静かに置く。図4のように、台上のP点から初速度
次に、台を床に固定する固定具を取り外し、台が床の上を自由に滑ることができるようにする。床と台との間の摩擦は無視できる。静止した台の上のQ点に小物体Bを静かに置く。図4のように、台上のP点から初速度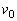 で小物体Aを右向きに滑らせると、小物体Aと小物体Bは衝突した。衝突直後の台の速度は0であった。小物体Aは、小物体Bとの衝突後、QR間の点で台との間の相対速度が0となり、以降は台と一体となって運動した。さらにその後、小物体Bは、QR間の点で台との間の相対速度が0となり、以降は台と一体となって右向きに速度
で小物体Aを右向きに滑らせると、小物体Aと小物体Bは衝突した。衝突直後の台の速度は0であった。小物体Aは、小物体Bとの衝突後、QR間の点で台との間の相対速度が0となり、以降は台と一体となって運動した。さらにその後、小物体Bは、QR間の点で台との間の相対速度が0となり、以降は台と一体となって右向きに速度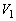 で運動した。
で運動した。
設問(5):速度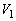 を、m,μ,
を、m,μ,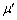 ,e,g,
,e,g,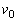 の中から適切なものを用いて表せ。
の中から適切なものを用いて表せ。
設問(6):小物体Aと台との間の相対速度が0となってから、小物体Bと台との間の相対速度が0となるまでの間の台の運動を考える。小物体Aと小物体Bが台に及ぼす力をすべて解答欄の図中に矢印で示し、それらの力の大きさを解答欄の図中に数式で記せ。解答に際しては、力の向きに留意して矢印を図示せよ。数式は、m,μ,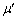 ,e,g,
,e,g,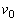 の中から適切なものを用いて表せ。
の中から適切なものを用いて表せ。 [解答へ]
早大理工物理'10年[2]
以下の問題の にあてはまる式、数字、文字、または語句を解答用紙の該当欄に記入せよ。
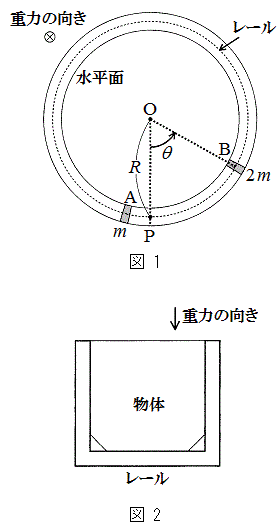 図1のように、水平な面内で、半径Rの円形をしたレール上にある質量mの物体Aと質量
図1のように、水平な面内で、半径Rの円形をしたレール上にある質量mの物体Aと質量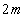 の物体Bの運動を考える。それぞれの物体は、図2の断面図のようにレールの壁および床とつねに接しており、レールの円周方向に沿ってのみ運動できる。物体A,Bとレールの壁、床との摩擦はない。運動を考えるとき、物体の大きさとレールの幅は無視できるものとする。点Oを中心にして、線分OPを基準とした回転角を
の物体Bの運動を考える。それぞれの物体は、図2の断面図のようにレールの壁および床とつねに接しており、レールの円周方向に沿ってのみ運動できる。物体A,Bとレールの壁、床との摩擦はない。運動を考えるとき、物体の大きさとレールの幅は無視できるものとする。点Oを中心にして、線分OPを基準とした回転角を で表し、
で表し、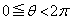 の範囲で定義する。重力加速度はgで表す。
の範囲で定義する。重力加速度はgで表す。
最初(時刻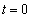 のとき)、物体Aは
のとき)、物体Aは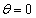 にあり、一定の速さ
にあり、一定の速さ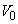 で反時計回りに等速円運動をしていた。また、
で反時計回りに等速円運動をしていた。また、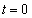 のとき、物体Bは
のとき、物体Bは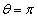 で静止していた。このとき、物体Aは、レールの底面および内壁から抗力を受け、全抗力の大きさは (1) となる。なお、壁から受ける抗力は、
で静止していた。このとき、物体Aは、レールの底面および内壁から抗力を受け、全抗力の大きさは (1) となる。なお、壁から受ける抗力は、 を向く。一方、物体Bに働くレールからの抗力の大きさは (3) である。二つの物体は、
を向く。一方、物体Bに働くレールからの抗力の大きさは (3) である。二つの物体は、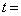 (4) で1回目の衝突をする。ここで、物体AとBの衝突は弾性衝突であり、衝突時間は短く無視できるものとすると、衝突後の物体Aの速さは (5) であり、物体Bの速さは (6) である。さらに、
(4) で1回目の衝突をする。ここで、物体AとBの衝突は弾性衝突であり、衝突時間は短く無視できるものとすると、衝突後の物体Aの速さは (5) であり、物体Bの速さは (6) である。さらに、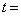 (7) のとき、2回目の衝突が
(7) のとき、2回目の衝突が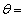 (8) で起こる。2回目の衝突後、物体Aの速さは (9) となり、物体Bの速さは (10) となる。以上のことから、衝突の起こるレール上の位置は全部で (11) カ所あり、2010回目の衝突は
(8) で起こる。2回目の衝突後、物体Aの速さは (9) となり、物体Bの速さは (10) となる。以上のことから、衝突の起こるレール上の位置は全部で (11) カ所あり、2010回目の衝突は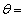 (12) で起こることがわかる。また、2010回目の衝突の直前の物体Aの速さは (13) であり、物体Bの速さは (14) である。
(12) で起こることがわかる。また、2010回目の衝突の直前の物体Aの速さは (13) であり、物体Bの速さは (14) である。
次に、物体Bの代わりに、レールの底面とのみ摩擦のある物体Cを用いた場合を考える。運動を考えるとき、物体の大きさとレールの幅は無視できるものとする。ここで、物体Cと底面との間の動摩擦係数を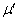 で表し、物体Cの質量は物体Aと等しくmとする。最初(
で表し、物体Cの質量は物体Aと等しくmとする。最初(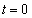 のとき)、物体Aは
のとき)、物体Aは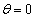 にあり、一定の速さ
にあり、一定の速さ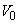 で反時計回りに等速円運動をしていた。このとき、物体Cは
で反時計回りに等速円運動をしていた。このとき、物体Cは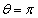 で静止していた。物体AとCの衝突は弾性衝突であり、衝突時間は短く無視できるものとする。さらに、衝突時間が短いため、物体Cに働く静止摩擦力による力積は無視できるものとする。1回目の衝突直後、運動している物体Cに働く摩擦力の大きさは (15) であり、物体Cが角度α
で静止していた。物体AとCの衝突は弾性衝突であり、衝突時間は短く無視できるものとする。さらに、衝突時間が短いため、物体Cに働く静止摩擦力による力積は無視できるものとする。1回目の衝突直後、運動している物体Cに働く摩擦力の大きさは (15) であり、物体Cが角度α 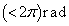 だけ進んだときの、二つの物体の運動エネルギーの和は (16) で与えられる。したがって、物体Cが物体Aと再度衝突するためには、速さ
だけ進んだときの、二つの物体の運動エネルギーの和は (16) で与えられる。したがって、物体Cが物体Aと再度衝突するためには、速さ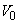 は (17) より大きくなければならない。
は (17) より大きくなければならない。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。