力学(万有引力)演習問題
名大物理'08年[1]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
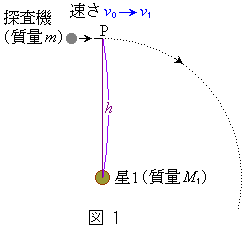1．図1のように宇宙空間を進む探査機が、点Pで探査機からnモルのアルゴンガス(単原子分子気体、1モルの質量
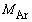)を、探査機の進む方向に瞬間的に噴射した。探査機は点Pで速さが
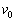から
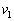に減速され、その後、星1のまわりを等速円運動した。ここで、アルゴンガス噴射前の探査機の質量mは星1の質量
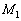に比べ充分に小さいものとする。以下の問いに答えよ。
(1) 探査機が星1のまわりを半径hで等速円運動するための速さ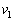
を求めよ。 (2) 噴射されたアルゴンガスの平均速度の大きさは、星1から見て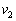
であった。探査機の速さを
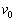から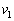
に減速するために噴射されるアルゴンガスのモル数nを
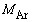，m，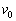
，
，
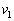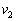を用いて表せ。ただし、噴射による探査機の質量変化も考慮せよ。 (3) 絶対温度Tのアルゴンガスにおける気体分子の熱運動の2乗平均速度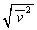
を、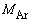
，R，Tを用いて表せ。 
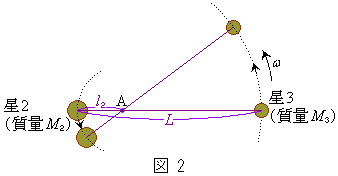2．図2のように、質量
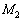の星2と質量
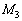の星3が、点Aを中心に、同じ角速度ω で等速円運動している。ここで、星2と星3の距離をL，点Aから星2までの距離を
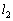とし、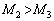
とする。また、星2と星3以外の天体の影響は無視できるものとして以下の問いに答えよ。
(1) 星2と星3について、それぞれ遠心力と万有引力のつり合いの式をG，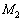
，
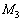，L，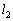
，ω を用いて表せ。 
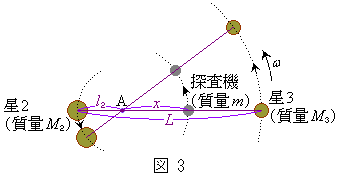次に、質量mの探査機を操作し、図3のように、点Aと星3を結ぶ線分上に置き、点Aを中心とする半径xで、星2と星3と同じ角速度ω で等速円運動させた。ただし、探査機の質量mは星2，星3の質量に比べ充分に小さいものとし、探査機の操作に伴う質量mの変化は無視できるものとする。
(3) 探査機に働く遠心力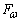
をm，ω，xを用いて表し、探査機に働く万有引力の合力
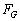をG，m，
，
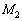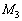，L，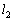
，xを用いて表せ。力の符号は点Aから星3の向きを正とする。 (4) 
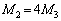とするとき、点Aと星3を結ぶ線分上では探査機に働く遠心力と万有引力の合力
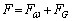がゼロとなる位置が
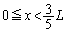の範囲には1つある。その位置を求めるため、合力FをG，m，
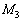，L，xを用いて表せ。さらに、
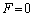となるxが存在する範囲を次の(ア)〜(ウ)の中から選び、その記号を記せ。 [解答へ]
早大教育物理'08年[1]
銀河系には、原子時計並の高い精度の周期で電波のパルスを放射しているパルサーと呼ばれる天体が存在する。その信号を地球で観測すると、地球の公転周期のためにパルスの到達する時間がずれ、その変化から以下のように太陽の質量を求めることができる。
(A) ケプラーの第3法則と太陽の質量
問1 地球は太陽を中心に円運動しているとし、その半径を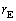
，公転周期を
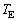とする。太陽が地球に及ぼす重力は地球が受ける向心力に等しい。
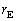と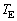
，および重力定数(万有引力定数)Gを用いて太陽の質量を表せ。 この式を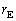
と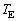
の関係式とみなすと、ケプラーの第3法則になっている。以下に示すように、長期にわたってパルスを記録する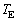と
と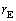
が求まり、太陽の質量が決定される。 
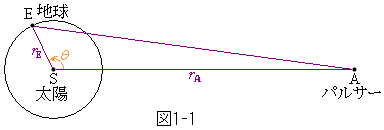(B) 到達時間の遅れ
簡単のためパルサーが地球の軌道面上にある場合を考える。パルサーの位置をA，太陽の位置をS，地球の位置はEとし、各天体間の距離を図1-1のように、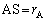
，
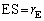とする。パルサーと太陽を結ぶ直線を基準として太陽に対する地球の公転運動の回転角を、図1-1のようにθ [ラジアン]と定める。
問2 天体の位置関係が図1-1のようなときに、地球とパルサーの距離EAを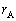
，
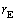，θ で表せ。 ヒント：余弦定理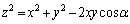 
問3 
に比べて
が十分に小さく、1と比べて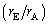
は無視できないが
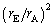はゼロとみなせる近似のもとに考える。地球Eで観測される特定のパルスの到達時刻は、太陽Sで観測される同じパルスの到達時刻を基準にすると
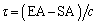遅れる。ただし、cは光速である。τ は正負どちらの値もとり得る。τ を
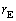，c，θ で表せ。 ヒント：pが1に比べ十分に小さいときqが実数であっても、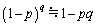
の近似が成立する。 問4 τ を時間tの関数として表そう。まず、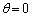
ラジアンとなる時刻を時間の原点
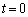にとり、θ を
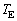とtで表せ。この結果と問3をもとに、τ を
，
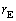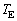，c，tで表せ。 問5 縦軸をτ にとり、横軸をtにとったグラフの概形を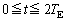
の範囲でかけ。縦軸には最大値と最小値を表す式を入れよ。 問6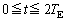 
の間で、地球に到達するパルスの時刻が太陽に到達する時刻に比べて最も早くなる(τ が最小となる)のは、tがいくらといくらのときか。すべて書き出せ。 問7 τ の季節変動を測定できれば、問5の理論曲線との比較により、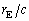
と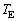
が精確に求まり、太陽の質量が問1より決まる。太陽の質量を1桁の精度で計算せよ。単位系はMKSでもcgsでもよいが、単位を書くこと。以下の数値を用いてよい。 測定から得られる値の近似値：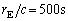
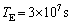
物理定数：重力定数(万有引力定数)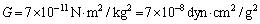 
光速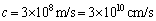 
問8 地球で観測されるパルスとパルスの間隔は季節によって異なる。観測されるパルスの間隔が一番長くなるtを、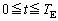
の範囲において求めよ。 [解答へ]
中大理工物理'08年[2]
次の文章の空欄にもっとも適した数式または数値を、それぞれ記せ。数値は有効数字2桁で答えよ。
楕円(だえん)とは、平面上で、ある2点(焦点という)からの距離の和が一定である点がえがく曲線である。ケプラーの第1法則として知られているように、太陽系の惑星の軌道は太陽を焦点の1つとする楕円である。ただし、地球や水星のような惑星の楕円軌道はほぼ円とみなしてよいものなので、以下では惑星の軌道は円軌道として計算することにする。
惑星の質量をm，円軌道の半径(惑星−太陽間の距離)をrとする。惑星が速さvで等速円運動しているとすると、向心力の大きさは (1) である。この力は太陽と惑星の間にはたらく万有引力であり、その大きさは、太陽の質量をM，万有引力定数をGとしたとき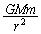
で与えられる。このことから、惑星の公転速度は
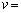(2) と定められる。この値vで軌道円周の長さ
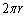を割ることによって、公転周期を求めることができる。
地球と太陽の間の距離を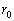
として、これを単位として考えることにする。太陽から木星までの距離を
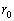のp倍とする。すると、木星の公転速度は地球の公転速度の (3) 倍であることになる。したがって、木星は (4) 年で太陽を1周する計算になる。
探査機を打ち上げて図1のような軌道で木星探査を実現させたい。
この探査機は木星と同様にケプラーの法則にしたがって運動するものとする。(つまり、太陽と探査機との間の万有引力は考慮するが、地球や木星といった惑星と探査機との間の万有引力は無視してよいものとする。)
このことから導かれることを、順に考えてみよう。
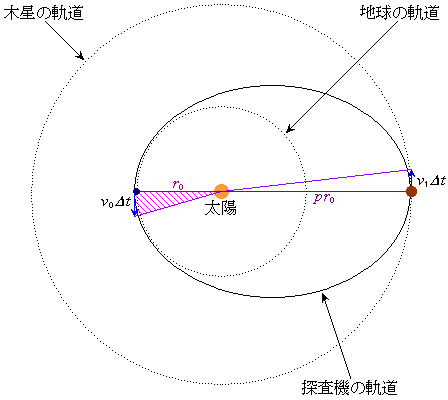まずケプラーの第1法則より、探査機の軌道も太陽を焦点の1つとする楕円軌道であることになる。地球の軌道上から出発したときの速さを
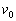とすると、探査機と太陽を結ぶ線分がある短い時間
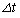の間にえがく面積は、近似的には図1の斜線を施した三角形の面積
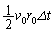で与えられる。探査機が木星の軌道近くを通過するときの速さを
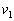とすると、ケプラーの第2法則(面積速度一定の法則)より
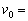(5)
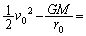(6) 
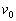は地球の公転速度の (7) 倍でなければならないことがわかる。
太陽から探査機までの距離は、地球の軌道上から出発したときに最小値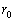
をとり、木星の軌道を通過するときに最大値
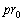をとる。この最小値と最大値の平均値
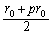を楕円軌道の半長軸という。ケプラーの第3法則より、公転周期の2乗は半長軸の3乗に比例する。したがって、探査機は地球の軌道上から出発して (8) 年後に木星の軌道に到達することになる。
具体的な数値を計算してみよう。木星−太陽間距離は地球−太陽間距離の約5.2倍である(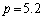
)。よって、木星の公転周期は約 (9) 年である。地球の公転速度は約
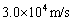である。これより、探査機が地球の軌道上から出発するときの速さは、
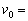(10) 
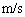，木星の軌道までの航行期間は約 (11) 年と求められる。ただし、
，
，
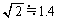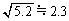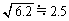として計算せよ。
[解答へ]
慶大理工物理'09年[1]
以下の文章中の に適切な数または式を記入しなさい。
人工衛星が地表すれすれを等速円運動するとき、その速さvは第一宇宙速度と呼ばれる。地球を質量M，半径Rの静止した球とし、万有引力定数をGとすると、万有引力が円運動の向心力となることから、第一宇宙速度は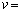
ア と表される。ただし空気抵抗はないものとする。一方、地上から打ち上げた人工衛星が無限の遠方にまで飛び去ってしまう最小の初速度は、第二宇宙速度と呼ばれる。これは、力学的エネルギー保存則により第一宇宙速度vの イ 倍であることがわかる。
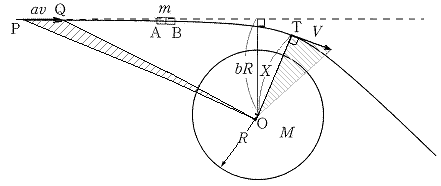図のように、宇宙船が地球の重力の作用だけで地球に戻ることを考える。質量mの宇宙船の速さは、地球から遠く離れた点Pにおいて、第一宇宙速度のa倍の速さ
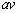である。点Pでは地球からの万有引力を無視できるとすると、宇宙船の力学的エネルギーは ウ である。点Pでの宇宙船の軌道を延長した直線と中心Oとの距離を半径Rのb倍とする。ただし、
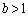である。このときの面積速度は、点Oと点P，および点Pから単位時間直進した後の宇宙船の位置Qの三点を結んでできる△OPQ(斜線)の面積である。したがって、面積速度は エ と求められる。
その後、宇宙船が地球に近づくと、万有引力のためにその軌道は地球の中心Oに向かって曲げられる。地球に最も近づいた位置を点Tとして、距離TOをX，点Tにおける宇宙船の速さをVとする、点Tでの面積速度は オ である。一方、点Tでは地球からの万有引力も考慮して、宇宙船の力学的エネルギーは カ となる。
以下では、宇宙船が地球をかすめるように通過する場合を考える。このとき最接近距離は地球の半径であるから、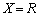
である。ケプラーの第二法則により、面積速度は一定、すなわち(エ)＝(オ)であることを用いると、再接近点での速さは
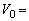キ である。さらに、力学的エネルギー保存則も成り立つので、(ウ)＝(カ)である。
これと(ア)の結果を用いると、変数としてaだけを含む式で、bは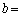
ク と表される。
しかし、この速さ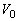
は第二宇宙速度より大きいため、宇宙船は地球をかすめた後、無限の遠方に飛び去ってしまう。そこで再接近点で宇宙船の一部分Bを進行方向前方に打ち出して、残りの部分Aに地表すれすれの等速円運動をさせた。このとき、AとBの質量が等しいとすると、Aから見たBを打ち出す速さは、
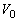とvを用いて ケ と表される。
[解答へ]
静岡大物理'10年[1]
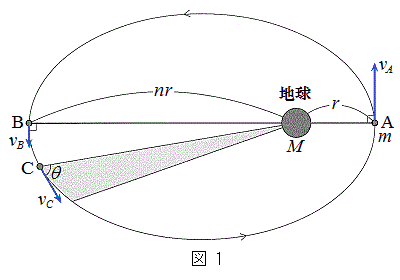図1に示すように地球と点Aの距離が
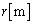，点Bとの距離がrのn倍である軌道上を周回する質量
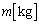の人工衛星がある。点Aを通過する人工衛星の速さを
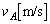，地球の質量を
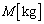，万有引力定数を
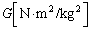とし、次の問いに答えよ。
問1 人工衛星が楕円軌道(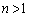
)で周回している場合を考える。ただし、地球と人工衛星との間にはケプラーの法則が成り立ち、地球の中心と人工衛星を結ぶ線分が単位時間に描く面積(面積速度という)が一定である。図1の点Cでは、この面積速度
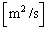の大きさは線分の長さ
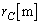，速さ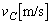
，線分と速度のなす角
を用いて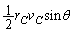
で表される。なお、線分ABは楕円の長軸であり、点A，点Bにおける速度の方向は線分ABに対して垂直である。 (1) 点Aにおける力学的エネルギー
を表せ。 (2) 点Aにおける面積速度をr，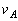
を用いて表せ。 (3) 点Bにおける速さ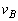
を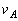
，nを用いて表せ。 (4) 点Aにおける速さ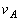
をn，G，M，rを用いて表せ。 (5) nが限りなく大きくなるときの速さ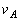
を求めよ。
問2 人工衛星が速さ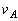
，半径rで等速円運動(
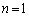)している場合を考える。ただし、地球は球体で自転による影響は無視できるものとする。 (1) 人工衛星に働く遠心力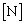
を表せ。 (2) 人工衛星に働く力のつり合いの式を表せ。
(3) 人工衛星の速さが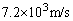
のとき、地表からの高さ
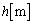はいくらか。ただし、地球の半径は
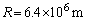，地表の重力加速度の大きさは
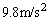とし、有効数字2桁で答えよ。 (4) 人工衛星の地表からの高さが地球の半径Rに等しいとき、人工衛星に働く重力加速度の大きさは地表の重力加速度の大きさの何倍か。有効数字2桁で答えよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
物理TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
を
，
，Lを用いて表し、角速度ω をG，
，
，Lを用いて表せ。
(イ) 
(ウ) 