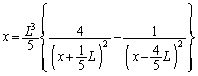���啨��'08�N[1]
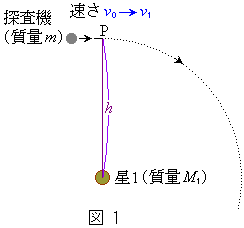 1�D�}1�̂悤�ɉF����Ԃ�i�ޒT���@���A�_P�ŒT���@����n�����̃A���S���K�X(�P���q���q�C�́A1�����̎���
1�D�}1�̂悤�ɉF����Ԃ�i�ޒT���@���A�_P�ŒT���@����n�����̃A���S���K�X(�P���q���q�C�́A1�����̎���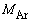 )���A�T���@�̐i�ޕ����ɏu�ԓI�ɕ��˂����B�T���@�͓_P�ő�����
)���A�T���@�̐i�ޕ����ɏu�ԓI�ɕ��˂����B�T���@�͓_P�ő�����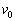 ����
����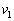 �Ɍ�������A���̌�A��1�̂܂����~�^�������B�����ŁA�A���S���K�X���ˑO�̒T���@�̎���m�͐�1�̎���
�Ɍ�������A���̌�A��1�̂܂����~�^�������B�����ŁA�A���S���K�X���ˑO�̒T���@�̎���m�͐�1�̎���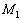 �ɔ�[���ɏ��������̂Ƃ���B�ȉ��̖₢�ɓ�����B
�ɔ�[���ɏ��������̂Ƃ���B�ȉ��̖₢�ɓ�����B
(1) �T���@����1�̂܂��ah�œ����~�^�����邽�߂̑���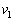 �����߂�B
�����߂�B (2) ���˂��ꂽ�A���S���K�X�̕��ϑ��x�̑傫���́A��1���猩��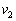 �ł������B�T���@�̑�����
�ł������B�T���@�̑�����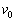 ����
���� �Ɍ������邽�߂ɕ��˂����A���S���K�X�̃�����n��
�Ɍ������邽�߂ɕ��˂����A���S���K�X�̃�����n��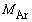 �Cm�C
�Cm�C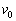 �C
�C �C
�C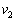 ��p���ĕ\���B�������A���˂ɂ��T���@�̎��ʕω����l������B
��p���ĕ\���B�������A���˂ɂ��T���@�̎��ʕω����l������B (3) ��Ή��xT�̃A���S���K�X�ɂ�����C�̕��q�̔M�^����2�敽�ϑ��x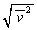 ���A
���A �CR�CT��p���ĕ\���B
�CR�CT��p���ĕ\���B 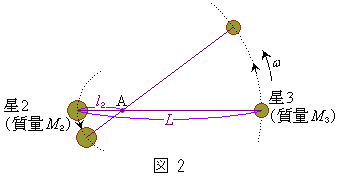 2�D�}2�̂悤�ɁA����
2�D�}2�̂悤�ɁA����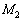 �̐�2�Ǝ���
�̐�2�Ǝ��� �̐�3���A�_A�𒆐S�ɁA�����p���xω �œ����~�^�����Ă���B�����ŁA��2�Ɛ�3�̋�����L�C�_A���琯2�܂ł̋�����
�̐�3���A�_A�𒆐S�ɁA�����p���xω �œ����~�^�����Ă���B�����ŁA��2�Ɛ�3�̋�����L�C�_A���琯2�܂ł̋�����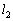 �Ƃ��A
�Ƃ��A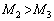 �Ƃ���B�܂��A��2�Ɛ�3�ȊO�̓V�̂̉e���͖����ł�����̂Ƃ��Ĉȉ��̖₢�ɓ�����B
�Ƃ���B�܂��A��2�Ɛ�3�ȊO�̓V�̂̉e���͖����ł�����̂Ƃ��Ĉȉ��̖₢�ɓ�����B
(1) ��2�Ɛ�3�ɂ��āA���ꂼ�ꉓ�S�͂Ɩ��L���͂̂荇���̎���G�C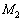 �C
�C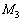 �CL�C
�CL�C �Cω ��p���ĕ\���B
�Cω ��p���ĕ\���B 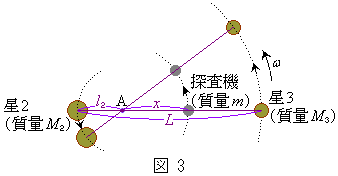 ���ɁA����m�̒T���@�𑀍삵�A�}3�̂悤�ɁA�_A�Ɛ�3�����Ԑ�����ɒu���A�_A�𒆐S�Ƃ��锼�ax�ŁA��2�Ɛ�3�Ɠ����p���xω �œ����~�^���������B�������A�T���@�̎���m�͐�2�C��3�̎��ʂɔ�[���ɏ��������̂Ƃ��A�T���@�̑���ɔ�������m�̕ω��͖����ł�����̂Ƃ���B
���ɁA����m�̒T���@�𑀍삵�A�}3�̂悤�ɁA�_A�Ɛ�3�����Ԑ�����ɒu���A�_A�𒆐S�Ƃ��锼�ax�ŁA��2�Ɛ�3�Ɠ����p���xω �œ����~�^���������B�������A�T���@�̎���m�͐�2�C��3�̎��ʂɔ�[���ɏ��������̂Ƃ��A�T���@�̑���ɔ�������m�̕ω��͖����ł�����̂Ƃ���B
(3) �T���@�ɓ������S��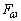 ��m�Cω�Cx��p���ĕ\���A�T���@�ɓ������L���͂̍���
��m�Cω�Cx��p���ĕ\���A�T���@�ɓ������L���͂̍���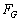 ��G�Cm�C
��G�Cm�C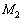 �C
�C �CL�C
�CL�C �Cx��p���ĕ\���B�͂̕����͓_A���琯3�̌����𐳂Ƃ���B
�Cx��p���ĕ\���B�͂̕����͓_A���琯3�̌����𐳂Ƃ���B (4) 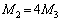 �Ƃ���Ƃ��A�_A�Ɛ�3�����Ԑ�����ł͒T���@�ɓ������S�͂Ɩ��L���͂̍���
�Ƃ���Ƃ��A�_A�Ɛ�3�����Ԑ�����ł͒T���@�ɓ������S�͂Ɩ��L���͂̍���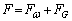 ���[���ƂȂ�ʒu��
���[���ƂȂ�ʒu��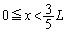 �͈̔͂ɂ�1����B���̈ʒu�����߂邽�߁A����F��G�Cm�C
�͈̔͂ɂ�1����B���̈ʒu�����߂邽�߁A����F��G�Cm�C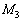 �CL�Cx��p���ĕ\���B����ɁA
�CL�Cx��p���ĕ\���B����ɁA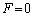 �ƂȂ�x�����݂���͈͂�����(�A)�`(�E)�̒�����I�сA���̋L�����L���B
�ƂȂ�x�����݂���͈͂�����(�A)�`(�E)�̒�����I�сA���̋L�����L���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1�D��2�D�͓Ɨ��Ȗ��ɂȂ��Ă��܂��B2�D(4)�́A�����I�ȍl�@�̗]�n���Ȃ��A�܂Ƃ��Ɍv�Z���Ă͎��Ԃ�������܂��B���œ����Ă��������ǂ������m��܂���B
1�D(1) �A���S���K�X���o��̒T���@�������� �Ƃ��āA�T���@������
�Ƃ��āA�T���@������ �̐�1��������L�����́A
�̐�1��������L�����́A �C����
�C����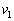 �������~�^����������T���@�������x��
�������~�^����������T���@�������x��
(2) �T���@�̃A���S���K�X���o�O���^������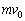 �C���o���������m����
�C���o���������m����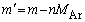 �ƂȂ葬����
�ƂȂ葬����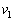 �ƂȂ�̂�
�ƂȂ�̂�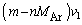 �ł��B
�ł��B ���o���ꂽ�A���S���K�X���^������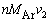 �ł��B�A���S���K�X���^�������T���@���^�����Ɠ��������ł��邱�Ƃɒ��ӂ��Ă��������B
�ł��B�A���S���K�X���^�������T���@���^�����Ɠ��������ł��邱�Ƃɒ��ӂ��Ă��������B
���o�O����^���ʕۑ����A ��  ......[��]
......[��]
(3) �A�{�K�h����(1�����̕����̕��q��)�� �Ƃ��āA�A���S���K�X1���q������������́A1������������
�Ƃ��āA�A���S���K�X1���q������������́A1������������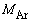 �Ȃ̂ŁA
�Ȃ̂ŁA �C����
�C���� �ʼn^������A���S���K�X1���q�̉^���G�l���M�[�́A
�ʼn^������A���S���K�X1���q�̉^���G�l���M�[�́A �ł��B�A���S���K�X�͒P���q���q���z�C���ł����āA����́A�{���c�}���萔��k�Ƃ���
�ł��B�A���S���K�X�͒P���q���q���z�C���ł����āA����́A�{���c�}���萔��k�Ƃ���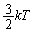 �ɓ�����(�C�̕��q�^���_���Q��)�A
�ɓ�����(�C�̕��q�^���_���Q��)�A  ���A
���A ......[��]
......[��]
2�D(1) ��2�Ɛ�3�̊Ԃɓ������L������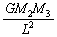
��2�������S���� (�����~�^�����Q��)�C��3�̉~�^�������a��
(�����~�^�����Q��)�C��3�̉~�^�������a��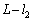 �Ȃ̂ŁA��3�������S����
�Ȃ̂ŁA��3�������S����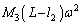
��2�ɂ��āA�͂̂荇���F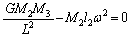 �@����@
�@����@
��3�ɂ��āA�͂̂荇���F �@����A
�@����A
(2) �@�C�A���A
��  ......[��]�@�ɑ������ƁA
......[��]�@�ɑ������ƁA �� 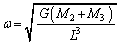 ......[��]
......[��]
(3) �T���@�ɓ������S���͐������ŁA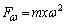 ......[��]
......[��] �T���@�Ɛ�2�������� �Ȃ̂ŁA�T���@����2��������L�����͕������ŁA
�Ȃ̂ŁA�T���@����2��������L�����͕������ŁA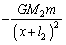
�T���@�Ɛ�3�������� �Ȃ̂ŁA�T���@����3��������L�����͐������ŁA
�Ȃ̂ŁA�T���@����3��������L�����͐������ŁA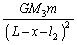
����āA���L�����������́A 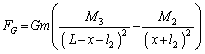 ......[��]
......[��]
(4) 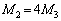 ��(2)�̌��ʂɑ������ƁA
��(2)�̌��ʂɑ������ƁA 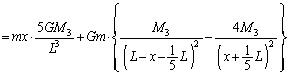
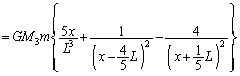 ......[��]
......[��]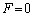 �Ƃ��āA
�Ƃ��āA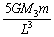 �Ŋ���ƁA
�Ŋ���ƁA�E�ӂ�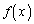 �Ƃ����āA
�Ƃ����āA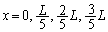 �̂Ƃ��A
�̂Ƃ��A ��x�̑召�W�ׂĂ݂܂��B
��x�̑召�W�ׂĂ݂܂��B ����āA �ƂȂ�x�����݂���͈͂́A
�ƂȂ�x�����݂���͈͂́A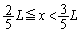 �ł����āA(�E) ......[��]
�ł����āA(�E) ......[��] �NjL�D��蕶�ɁAF���[���ƂȂ�ʒu��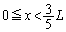 �͈̔͂ɂ�1����A�Ə����Ă���̂ŁA����ŗǂ��킯�ł����A
�͈̔͂ɂ�1����A�Ə����Ă���̂ŁA����ŗǂ��킯�ł����A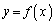 �̃O���t��
�̃O���t��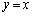 �ɂ���݂��悤�ɕω����镡�G�Ȋ����ƁA��L�̎�����������͉��Ƃ������Ȃ����ƂɂȂ�܂��B�����ł́A�ꉞ
�ɂ���݂��悤�ɕω����镡�G�Ȋ����ƁA��L�̎�����������͉��Ƃ������Ȃ����ƂɂȂ�܂��B�����ł́A�ꉞ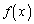 �̕ω����m���߂Ă������Ƃɂ��܂��B
�̕ω����m���߂Ă������Ƃɂ��܂��B 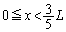 �ɂ����āA
�ɂ����āA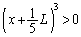 �C
�C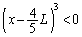 �Ȃ̂ŁA
�Ȃ̂ŁA �ł��B����āA���͈̔͂�
�ł��B����āA���͈̔͂�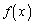 �͒P�������ł�(���̑������Q��)�Bx�̕��͒P�������Ȃ̂ŁA
�͒P�������ł�(���̑������Q��)�Bx�̕��͒P�������Ȃ̂ŁA�ł���A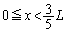 �ɂ����āA������
�ɂ����āA������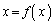 �́A
�́A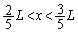 �͈̔͂ɂ���1�̉������ƒf��ł��܂��B
�͈̔͂ɂ���1�̉������ƒf��ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@����TOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 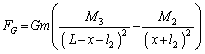 ......[��]
......[��]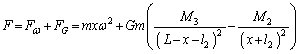
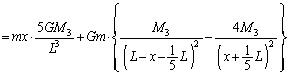
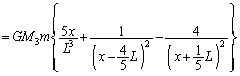 ......[��]
......[��]