共通テスト数学IA '22年第2問
[1] p,qを実数とする。
花子さんと太郎さんは、次の二つの2次方程式について考えている。
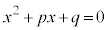 ・・・①
・・・①
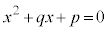 ・・・②
・・・②①または②を満たす実数xの個数をnとおく。
(2) 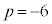 のとき、
のとき、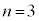 になる場合を考える。
になる場合を考える。
花子:例えば、①と②をともに満たす実数xがあるときは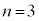 になりそうだね。
になりそうだね。 太郎:それをaとしたら、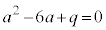 と
と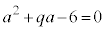 が成り立つよ。
が成り立つよ。 花子:なるほど。それならば、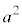 を消去すれば、aの値が求められそうだね。
を消去すれば、aの値が求められそうだね。 太郎:確かにaの値が求まるけど、実際に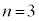 になっているかどうかの確認が必要だね。
になっているかどうかの確認が必要だね。 花子:これ以外にも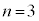 となる場合がありそうだね。
となる場合がありそうだね。 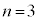 となるqの値は
となるqの値はである。ただし、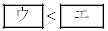 とする。
とする。 (3) 花子さんと太郎さんは、グラフ表示ソフトを用いて、①,②の左辺をyとおいた2次関数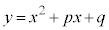 と
と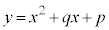 のグラフの動きを考えている。
のグラフの動きを考えている。 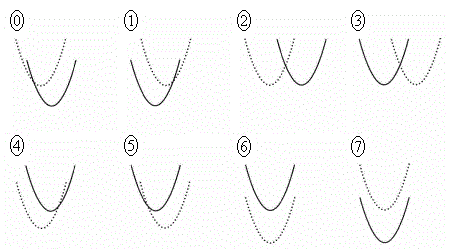
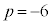 に固定したまま、qの値だけを変化させる。
に固定したまま、qの値だけを変化させる。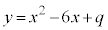 ・・・③
・・・③
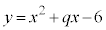 ・・・④
・・・④(4) 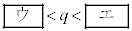 とする。全体集合Uを実数全体の集合とし、Uの部分集合A,Bを
とする。全体集合Uを実数全体の集合とし、Uの部分集合A,Bを とする。Uの部分集合Xに対し、Xの補集合を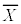 と表す。このとき、次のことが成り立つ。
と表す。このとき、次のことが成り立つ。  ,
, の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) 必要条件であるが、十分条件ではない
必要条件であるが、十分条件ではない 十分条件であるが、必要条件ではない
十分条件であるが、必要条件ではない 必要十分条件である
必要十分条件である 必要条件でも十分条件でもない
必要条件でも十分条件でもない
[2] 日本国外における日本語教育の状況を調べるために、ある行政機関では「海外日本語教育機関調査」を実施しており、各国における教育機関数、教員数、学習者数が調べられている。2018年度において学習者数が5000人以上の国と地域(以下、国)は29か国であった。これら29か国について、2009年度と2018年度のデータが得られている。
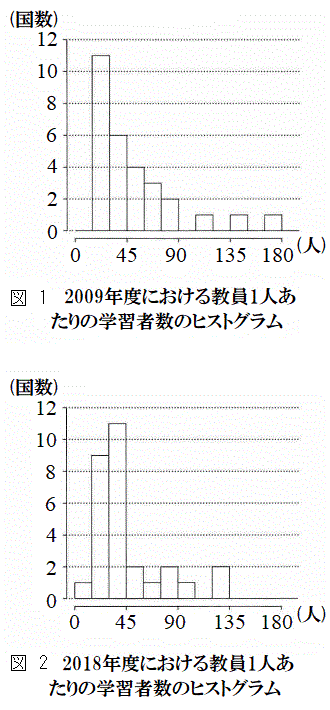 (1) 各国において、学習者数を教員数で割ることにより、国ごとの「教員1人あたりの学習者数」を算出することができる。図1と図2は、2009年度および2018年度における「教員1人あたりの学習者数」のヒストグラムである。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
(1) 各国において、学習者数を教員数で割ることにより、国ごとの「教員1人あたりの学習者数」を算出することができる。図1と図2は、2009年度および2018年度における「教員1人あたりの学習者数」のヒストグラムである。これら二つのヒストグラムから、9年間の変化に関して、後のことが読み取れる。なお、ヒストグラムの各階級の区間は、左側の数値を含み、右側の数値を含まない。
・2009年度と2018年度の中央値が含まれる階級の階級値を比較すると、 。
。 ・2009年度と2018年度の第1四分位数が含まれる階級の階級値を比較すると、 。
。 ・2009年度と2018年度の第3四分位数が含まれる階級の階級値を比較すると、 。
。 ・2009年度と2018年度の範囲を比較すると、 。
。 ・2009年度と2018年度の四分位範囲を比較すると、 。
。  ~
~ の解答群(同じものを繰り返し選んでもよい。)
の解答群(同じものを繰り返し選んでもよい。) 2018年度の方が小さい
2018年度の方が小さい 2018年度の方が大きい
2018年度の方が大きい 両者は等しい
両者は等しい これら二つのヒストグラムからだけでは両者の大小を判断できない
これら二つのヒストグラムからだけでは両者の大小を判断できない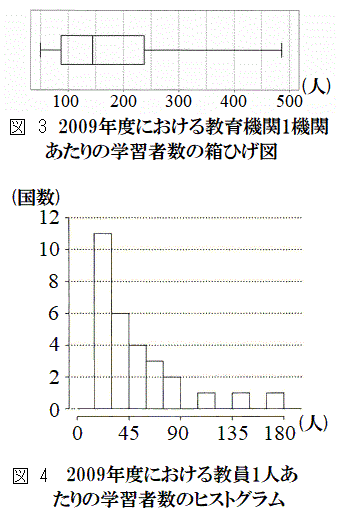 (2) 各国において、学習者数を教育機関数で割ることにより、「教育機関1機関あたりの学習者数」も算出した。図3は、2009年度における「教育機関1機関あたりの学習者数」の箱ひげ図である。
(2) 各国において、学習者数を教育機関数で割ることにより、「教育機関1機関あたりの学習者数」も算出した。図3は、2009年度における「教育機関1機関あたりの学習者数」の箱ひげ図である。
(3) 各国における2018年度の学習者数を100としたときの2009年度の学習者数S,および、各国における2018年度の教員数を100としたときの2009年度の教員数Tを算出した。
例えば、学習者数について説明すると、ある国において、2009年度が44272人、2018年度が174521人であった場合、2009年度の学習者数Sは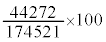 より
より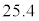 と算出される。
と算出される。
表1はSとTについて、平均値、標準偏差および共分散を計算したものである。ただし、SとTの共分散は、Sの偏差とTの偏差の積の平均値である。
表1の数値が四捨五入していない正確な値であるとして、SとTの相関係数を求めると である。
である。
表1 平均値、標準偏差および共分散
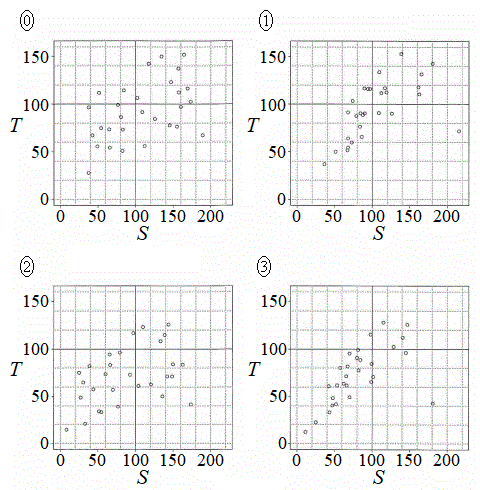 (4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度のS (横軸)とT (縦軸)の散布図は
(4) 表1と(3)で求めた相関係数を参考にすると、(3)で算出した2009年度のS (横軸)とT (縦軸)の散布図は である。
である。 については、最も適当なものを、右図の
については、最も適当なものを、右図の ~
~ のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
のうちから一つ選べ。なお、これらの散布図には、完全に重なっている点はない。
注.原問題文には弊塾とは関係のない実在の団体名が含まれるため、問題文を改変しました。問題を解く上では影響ありません。原問題文は、大学入試センターの過去問を参照してください。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 [1]で時間を使いすぎると[2]のヒストグラムや散布図を丁寧に調べる余裕がなくなります。
[1] 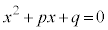 ・・・①
・・・① 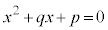 ・・・②
・・・②
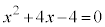 ∴
∴ 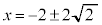
②は、
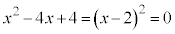 ∴
∴ 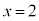
よって、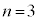 です。
です。
ア 3 ......[答]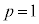 ,
,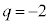 のとき、①は、
のとき、①は、 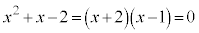 ∴
∴ 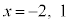
②は、
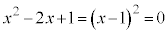 ∴
∴ 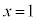
よって、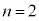 です。
です。
イ 2 ......[答] (2) 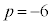 のとき、①,②は、それぞれ、
のとき、①,②は、それぞれ、 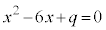 ・・・⑤
・・・⑤
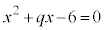 ・・・⑥
・・・⑥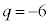 のときは、⑤と⑥は一致し
のときは、⑤と⑥は一致し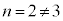 です。
です。
⑤と⑥が共通解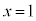 を持つとき、⑤に代入して、
を持つとき、⑤に代入して、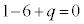 より、
より、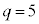
このとき、⑤は、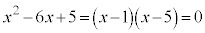 ∴
∴ 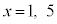 ⑥は、
⑥は、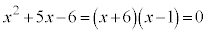 ∴
∴ 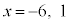 よって、確かに
よって、確かに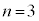 です。
です。
⑤,⑥が共通解を持たない場合は、どちらかが重解を持ち、他がこの重解とは異なる2解を持つとき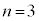 となります。⑤が重解を持つ場合、判別式:
となります。⑤が重解を持つ場合、判別式: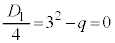 より
より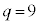 で重解は3です。このとき⑥は、
で重解は3です。このとき⑥は、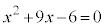 ∴
∴ 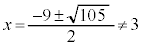 よって、このときも
よって、このときも
⑥の判別式: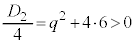 より、⑥が重解を持つことはありません。よって、
より、⑥が重解を持つことはありません。よって、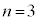 となるqは、
となるqは、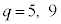
ウ 5 エ 9 ......[答]④は、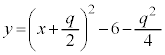 (
(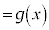 とします)より、軸は
とします)より、軸は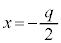 ,頂点は
,頂点は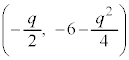 (2次関数を参照)③で、qの値を1から増加させると、頂点は
(2次関数を参照)③で、qの値を1から増加させると、頂点は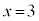 上を、y座標が大きくなる方向に移動します。
上を、y座標が大きくなる方向に移動します。
オ 6 ......[答]④で、qの値を1から増加させると、頂点は、x座標、y座標ともに小さくなる方向に移動します。
カ 1 ......[答] (4) 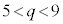 のとき、③の頂点のy座標は、
のとき、③の頂点のy座標は、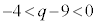 の範囲にあります。
の範囲にあります。 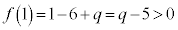 なので、
なので、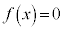 は、
は、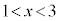 の範囲に解αを持ちます。また、放物線の軸に関する対称性より
の範囲に解αを持ちます。また、放物線の軸に関する対称性より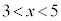 の範囲に解βを持ちます(2次方程式の一般論を参照)。つまり、
の範囲に解βを持ちます(2次方程式の一般論を参照)。つまり、④の軸は、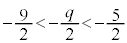 より
より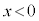 の範囲にあります。④の頂点のy座標は
の範囲にあります。④の頂点のy座標は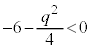 ,
,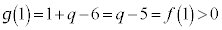 なので、③のグラフと④のグラフは直線
なので、③のグラフと④のグラフは直線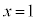 上に交点を持ち、
上に交点を持ち、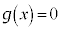 は、
は、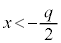 ,
,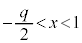 の範囲に、それぞれ解γ,δを持ちます。つまり、
の範囲に、それぞれ解γ,δを持ちます。つまり、 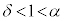 に注意して、
に注意して、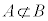 ,
,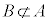 ,
,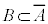
以上より、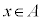 は、
は、 であるための必要条件でも十分条件でもなく(条件・命題を参照)、
であるための必要条件でも十分条件でもなく(条件・命題を参照)、
キ 3 ......[答]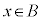 は、
は、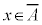 であるための十分条件だが必要条件ではなく、
であるための十分条件だが必要条件ではなく、
ク 1 ......[答]
[2](1) データの大きさが、2009年、2018年ともに、29なので、中央値は15番目の値、第1四分位数は7番目と8番目の平均値、第3四分位数は22番目と23番目の平均値です(四分位数を参照)。 2009年では、第1四分位数は15~30,中央値は30~45,第3四分位数は60~75の階級に位置します。
2018年では、第1四分位数は15~30,中央値は30~45,第3四分位数は45~60の階級に位置します。
・2009年と2018年の中央値が含まれる階級は一致します。
ケ 2 ......[答]
・2009年と2018年の第1四分位数が含まれる階級は一致します。
コ 2 ......[答]
・第3四分位数の階級値は2018年の方が小さくなります。
サ 0 ......[答]
・範囲は、2009年が165-30=135以上、2018年が135-0=135未満で2018年の方が小さくなります。
シ 0 ......[答]
・四分位範囲は、2009年が30以上60未満、2018年が15以上45未満で、これだけではどちらが大きいか分かりません。
ス 3 ......[答]
(2) 4つの散布図はいずれも教員1人あたりの学習者数の、最大値、最小値、中央値が一致します。図3の箱ひげ図を見ると教育機関1機関あたりの学習者数について、第1四分位数はほぼ90、第3四分位数は240程度です。散布図 は、横軸の90以下は5個未満で不適。
は、横軸の90以下は5個未満で不適。 は、横軸90以下は6個以下で不適、
は、横軸90以下は6個以下で不適、 は横軸の240以上が8個以上あって不適。
は横軸の240以上が8個以上あって不適。 セ 2 ......[答]
ソ 0 タチ 63 ......[答]
(4) 相関係数が0.63なのでかなり強い正の相関があります。これで か
か になりますが、
になりますが、 はSの平均が100以上、Tの平均が80以上で不適、
はSの平均が100以上、Tの平均が80以上で不適、 はTの最大が130未満、Tの最小が20未満で、
はTの最大が130未満、Tの最小が20未満で、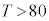 が11個、
が11個、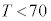 が13個でTの平均が70以下になり不適。
が13個でTの平均が70以下になり不適。 はSの平均が90以上、Tの平均が90以上で不適。
はSの平均が90以上、Tの平均が90以上で不適。 ツ 3 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 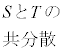
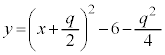 (
(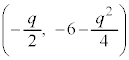 (2次関数を参照)
(2次関数を参照)