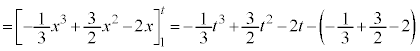共通テスト数学IIB '22年第2問
[1] aを実数とし、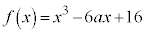 とおく。
とおく。
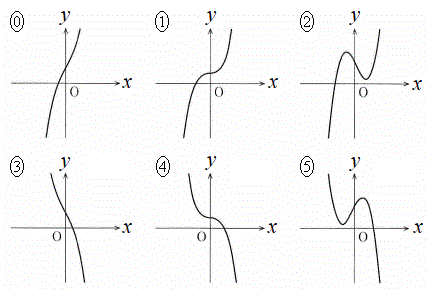 (1)
(1)  のグラフの概形は
のグラフの概形はである。
 ,
,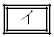 については、最も適当なものを、右図の
については、最も適当なものを、右図の 〜
〜 のうちから一つずつ選べ、ただし、同じものを繰り返し選んでもよい。
のうちから一つずつ選べ、ただし、同じものを繰り返し選んでもよい。
(2) 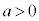 とし、pを実数とする。座標平面上の曲線
とし、pを実数とする。座標平面上の曲線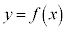 と直線
と直線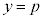 が3個の共有点をもつようなpの値の範囲は
が3個の共有点をもつようなpの値の範囲は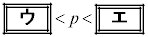 である。
である。 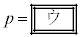 のとき、曲線
のとき、曲線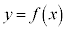 と直線
と直線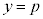 は2個の共有点をもつ。それらのx座標をq,r (
は2個の共有点をもつ。それらのx座標をq,r (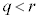 )とする。曲線
)とする。曲線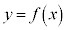 と直線
と直線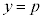 が点
が点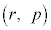 で接することに注意すると
で接することに注意すると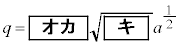 ,
,
と表せる。
 ,
, の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい)
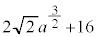

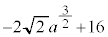

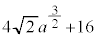

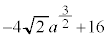

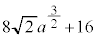

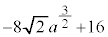
(3) 方程式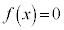 の異なる実数解の個数をnとする。次の
の異なる実数解の個数をnとする。次の 〜
〜 のうち、正しいものは
のうち、正しいものは と
と である。
である。  ,
, の解答群(解答の順序は問わない)
の解答群(解答の順序は問わない)
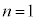 ならば
ならば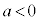

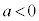 ならば
ならば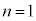

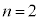 ならば
ならば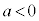

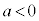 ならば
ならば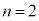

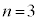 ならば
ならば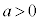

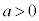 ならば
ならば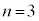
[2] 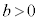 とし、
とし、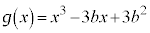 ,
,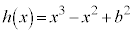 とおく。座標平面上の曲線
とおく。座標平面上の曲線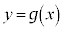 を
を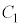 ,曲線
,曲線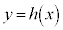 を
を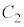 とする。
とする。 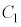 と
と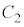 は2点で交わる。これらの交点のx座標をそれぞれα,β (
は2点で交わる。これらの交点のx座標をそれぞれα,β (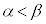 )とすると、
)とすると、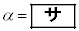 ,
, である。
である。
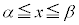 の範囲で
の範囲で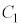 と
と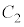 で囲まれた図形の面積をSとする。また、
で囲まれた図形の面積をSとする。また、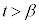 とし、
とし、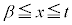 の範囲で
の範囲で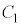 と
と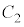 および
および
直線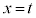 で囲まれた図形の面積をTとする。
で囲まれた図形の面積をTとする。
このときであるので
が得られる。
したがって、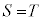 となるのは
となるのは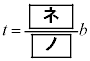 のときである。
のときである。
 〜
〜 の解答群(同じものを繰り返し選んでもよい)
の解答群(同じものを繰り返し選んでもよい)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 最後のところはやや計算が面倒で、簡便な方法で済ませないと完答は難しくなります。
[1] 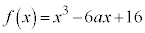
(1) 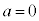 のとき、
のとき、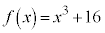 ,
,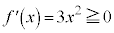 より、
より、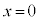 において接線の傾きが0で、それ以外では接線の傾きは正です。そうなっているグラフは
において接線の傾きが0で、それ以外では接線の傾きは正です。そうなっているグラフは 。
。 ア 1 ......[答]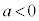 のとき、
のとき、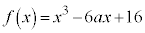 ,
,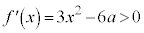 より、つねに接線の傾きは正です。そうなっているグラフは
より、つねに接線の傾きは正です。そうなっているグラフは 。
。
イ 0 ......[答] (2) 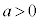 のとき、
のとき、 より、増減表は、これより、曲線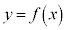 と直線
と直線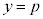 が3個の共有点をもつのは、
が3個の共有点をもつのは、 オ − カ 2 キ 2 ク 2 ......[答]
(3) (1)より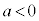 ならば
ならば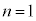 です。ですが、
です。ですが、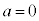 のときにも
のときにも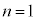 です。
です。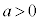 であっても、
であっても、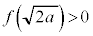 であれば
であれば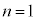 です。ですが、
です。ですが、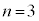 であれば
であれば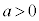 です。
です。 ケ 1 コ 4 ......[答]
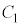 と
と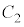 の方程式を連立すると、
の方程式を連立すると、サ b シ 2b ......[答]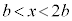 ,つまり、
,つまり、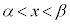 においては
においては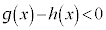 ,
,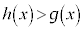
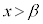 においては、
においては、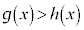
よって、 チツ −1 テ 6 ト 9 ナニ 12 ヌ 5 ......[答]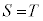 とすると、
とすると、 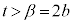 なので、
なので、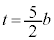
ネ 5 ノ 2 ......[答]注.最後のチツテトナニヌのところは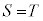 の式のbの入り方から見て、
の式のbの入り方から見て、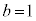 として計算し、
として計算し、 として計算するとよいでしょう。
とおくと、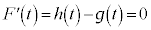 (定積分と微分を参照)の解が
(定積分と微分を参照)の解が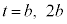 で、ここで、
で、ここで、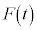 は極値をとります。3次方程式
は極値をとります。3次方程式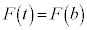 のb以外の解をc,3次方程式
のb以外の解をc,3次方程式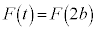 の
の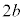 以外の解をdとして、d,b,
以外の解をdとして、d,b,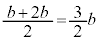 ,
,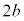 ,cが等間隔に並ぶこと(3次関数のグラフを参照)を知っていれば、
,cが等間隔に並ぶこと(3次関数のグラフを参照)を知っていれば、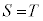 となるt は
となるt は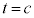 なので、ほぼ計算なしで、
なので、ほぼ計算なしで、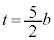 であることがわかります。
であることがわかります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 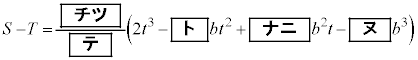
 のときである。
のときである。