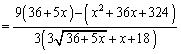�F�{�嗝���w'07�N���[3]
����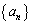 ��
��
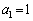 �C
�C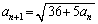 �@(
�@(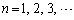 )
)
�ŗ^�����Ă���Ƃ���B�܂��A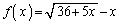 �Ƃ��Ax�Ɋւ��������
�Ƃ��Ax�Ɋւ��������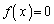 �̐��̉���a�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�̐��̉���a�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) a�̒l�����߂�B
(2) ���ׂĂ̐��̐���n�ɂ��āA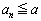 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (3) 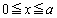 �ɂ����āA
�ɂ����āA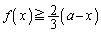 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (4) 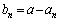 �Ƃ���Ƃ��A���ׂĂ̐��̐���n�ɂ��āA
�Ƃ���Ƃ��A���ׂĂ̐��̐���n�ɂ��āA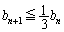 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (5) 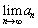 �̒l�����߂�B
�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@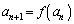 �^�C�v���Q�������Ɍ������߂���ł��B
�^�C�v���Q�������Ɍ������߂���ł��B
(1) 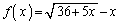
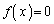 �Ƃ���ƁA
�Ƃ���ƁA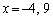
���̉�a�́A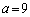 ......[��]
......[��]
(2) 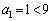 �ł��B
�ł��B 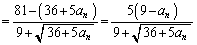 �@����@
�@����@���A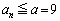 �ł���A
�ł���A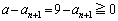 �C�܂�A
�C�܂�A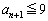 �ł��B
�ł��B
����ċA�[�I��(���w�I�A�[�@���Q��)�A���ׂĂ̐��̐���n�ɂ��āA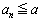 �ł��B�@(�ؖ��I)
�ł��B�@(�ؖ��I)
(3) 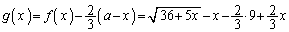
(4) 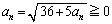 ��(2)�̌��ʂ����킹�āA
��(2)�̌��ʂ����킹�āA ������(3)�̌��ʂɂ�����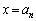 �Ƃ���ƁA
�Ƃ���ƁA �� 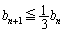 �@(�ؖ��I)�ʉ��@�@���A
�@(�ؖ��I)�ʉ��@�@���A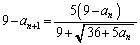
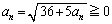 ���A
���A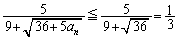
�� 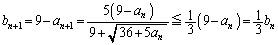 �Ƃ��邱�Ƃ��ł��܂��B
�Ƃ��邱�Ƃ��ł��܂��B
(5) (2)���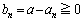
�NjL�D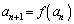 �^�C�v�̑Q�����ŗ^�����鐔��
�^�C�v�̑Q�����ŗ^�����鐔��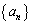 �ł́A
�ł́A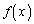 ������͈�
������͈�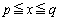 ��
��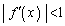 �ł����āA
�ł����āA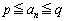 ��
��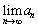 �����݂���A������
�����݂���A������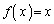 ��
��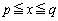 �ɂ��������α�Ƃ��āA
�ɂ��������α�Ƃ��āA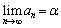 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ȃ��Ȃ�A���ϒl�̒藝���A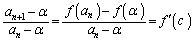 �C
�C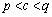 ���݂�������c�����݂��āA
���݂�������c�����݂��āA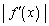 ��
��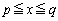 �ɂ�����ő�l��m�Ƃ���A
�ɂ�����ő�l��m�Ƃ���A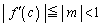 �ŁA
�ŁA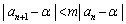 ���A
���A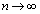 �̂Ƃ�
�̂Ƃ�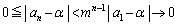 �ƂȂ邩��ł��B
�ƂȂ邩��ł��B
�{��ł́A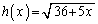 �Ƃ����ƁA
�Ƃ����ƁA
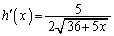 �C
�C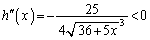
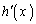 ���P���������ŁA
���P���������ŁA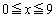 �ɂ����ẮA
�ɂ����ẮA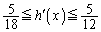 �Ȃ̂ŁA
�Ȃ̂ŁA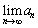 �́A
�́A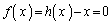 �̉�9�ɂȂ�܂��B
�̉�9�ɂȂ�܂��B
�{���(4)�ɏo�Ă���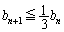 ��
��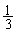 �Ƃ����l�́A
�Ƃ����l�́A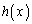 ��
��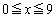 �ɂ����镽�ϕω���
�ɂ����镽�ϕω���
�ł����āA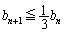 �́A
�́A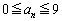 �ł���Ε��ϕω����ɂ��āA
�ł���Ε��ϕω����ɂ��āA
�ł��邱�Ƃ��Ӗ����Ă��܂��B�Ȃ��A�k�嗝�n'08�N�O��[3]���Q�Ƃ��Ă��������B
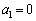 �C
�C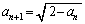 �Ƃ����Q�����ŗ^�����鐔��̋Ɍ�
�Ƃ����Q�����ŗ^�����鐔��̋Ɍ�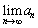 �����߂���������Ό������܂����A
�����߂���������Ό������܂����A
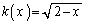 �C
�C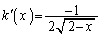
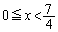 �ɂ����āA
�ɂ����āA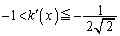
�ƂȂ�A
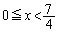 ���݂�������
���݂�������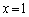 �Ȃ̂ŁA
�Ȃ̂ŁA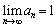 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ƃ������ɂ���1�ɋ߂Â��Ă����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B