�k�嗝�n���w'08�N�O��[3]
��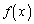 ��
��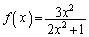 �Ƃ���B
�Ƃ���B
(1) 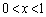 �Ȃ�A
�Ȃ�A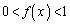 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (2) 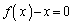 �ƂȂ�x�����ׂċ��߂�B
�ƂȂ�x�����ׂċ��߂�B (3) 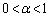 �Ƃ��A����
�Ƃ��A����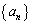 ��
�� �Ƃ���Bα�̒l�ɉ����āA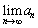 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��^�p�^�[���ő��U�����A�Ǝv���ƁA�u�Â��v�ƌ����Ă��܂����ł��B
���嗝�n'84�N[6]�ɁA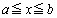 �Œ�`���ꂽ��
�Œ�`���ꂽ��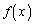 ���A
���A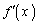 �C
�C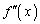 �������A
�������A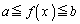 �C1��菬��������萔k�ɂ���
�C1��菬��������萔k�ɂ���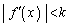 �C���݂����Ƃ��ɁA������
�C���݂����Ƃ��ɁA������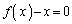 ��
��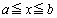 �͈̔͂ɂ���1�̉�
�͈̔͂ɂ���1�̉�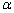 �������A
�������A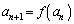 �Œ�`����鐔��
�Œ�`����鐔��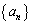 �ɂ��āA
�ɂ��āA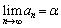 �ƂȂ�(����̋Ɍ����Q��)���Ƃ��A�Ƃ�����肪����܂����B
�ƂȂ�(����̋Ɍ����Q��)���Ƃ��A�Ƃ�����肪����܂����B
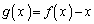 �Ƃ����ƁA
�Ƃ����ƁA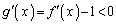 ���A
���A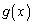 ��
��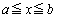 �ɂ������������ŁA
�ɂ������������ŁA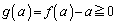 �C
�C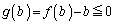 ���A
���A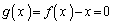 �́A
�́A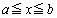 �͈̔͂ɂ���1�̉�α�������܂��B
�͈̔͂ɂ���1�̉�α�������܂��B
����̊e��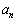 �̒���
�̒���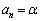 �ƂȂ鍀������A
�ƂȂ鍀������A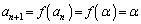 ���An�ȏ�̐���n�ɂ���
���An�ȏ�̐���n�ɂ���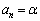 �ƂȂ��Ă��܂��̂ŁA
�ƂȂ��Ă��܂��̂ŁA �ł��B
�ł��B
���ׂĂ̍��ɂ���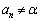 �ł���A�^����ꂽ����ɂ���āA���ϒl�̒藝�ɂ��A
�ł���A�^����ꂽ����ɂ���āA���ϒl�̒藝�ɂ��A
���݂�������c���K�����݂��܂��B���̍��ӂ́A
�ł���A����ɂ��A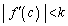 �Ȃ̂ŁA
�Ȃ̂ŁA
����āA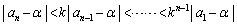
�� 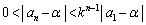
������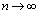 �Ƃ���A
�Ƃ���A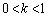 ���
���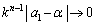 (���䐔��̋Ɍ����Q��)�ƁA�͂��݂����̌����ɂ���āA
(���䐔��̋Ɍ����Q��)�ƁA�͂��݂����̌����ɂ���āA
�ƂȂ�܂��B
���̖��ȍ~�A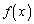 �ɋ�̓I�Ȋ��̌`��^���A
�ɋ�̓I�Ȋ��̌`��^���A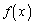 �̑����������
�̑����������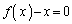 �̉��Ȃǂׂ����A
�̉��Ȃǂׂ����A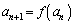 �Œ�`����鐔��̋Ɍ�
�Œ�`����鐔��̋Ɍ�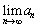 �����߂�����A�Ƃ��������悭��������悤�ɂȂ�܂����B��L�̂悤�����ϒl�̒藝���g���ΊȒP�ɂ���ł��܂��̂ŁA��@�p�^�[�����o���Ă��܂��Ίm���ɓ��_���ɂł�����ł����B�k��ł��A'95�N���n���[3]�ɂ����ďo�肳�ꂽ���Ƃ�����܂��B
�����߂�����A�Ƃ��������悭��������悤�ɂȂ�܂����B��L�̂悤�����ϒl�̒藝���g���ΊȒP�ɂ���ł��܂��̂ŁA��@�p�^�[�����o���Ă��܂��Ίm���ɓ��_���ɂł�����ł����B�k��ł��A'95�N���n���[3]�ɂ����ďo�肳�ꂽ���Ƃ�����܂��B
���́A2���ԑQ����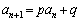 ��
��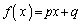 �Ƃ݂Ȃ��A���̃^�C�v��1��ɉ߂��܂���B
�Ƃ݂Ȃ��A���̃^�C�v��1��ɉ߂��܂���B
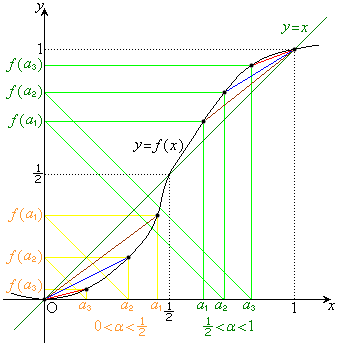 ���̖k��̖����A���̒�^�p�^�[���̂悤�Ɍ�����̂ł����A
���̖k��̖����A���̒�^�p�^�[���̂悤�Ɍ�����̂ł����A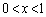 �ɂ�����
�ɂ�����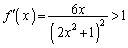 �ƂȂ�ꍇ������̂ŁA��їE��ŕ��ϒl�̒藝���g���ē��Ă������n�߂Ă��s���l�܂�܂��B����́A
�ƂȂ�ꍇ������̂ŁA��їE��ŕ��ϒl�̒藝���g���ē��Ă������n�߂Ă��s���l�܂�܂��B����́A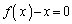 �̉����A
�̉����A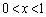 �ɂ����Ă�
�ɂ����Ă�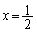 �����ł����A
�����ł����A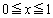 �ɂ����Ă�
�ɂ����Ă�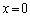 �C
�C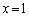 �����ɂȂ��Ă��āA�����ɂ���ẮA����0��1�ɋ߂Â��ꍇ������悤�ɖ�肪����Ă��邩��ł��B�E�}�̃O���t�ŁA
�����ɂȂ��Ă��āA�����ɂ���ẮA����0��1�ɋ߂Â��ꍇ������悤�ɖ�肪����Ă��邩��ł��B�E�}�̃O���t�ŁA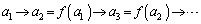 �Ƃ��ǂ�Ƃǂ��Ȃ邩���l���Ă݂Ă��������B
�Ƃ��ǂ�Ƃǂ��Ȃ邩���l���Ă݂Ă��������B
�ł����A���̖����A���ϒl�̒藝���g���Ȃ��Ă��A���ϕω������l����Γ��l�̔��z�ʼn������܂��B
�t�����l���āA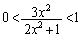
����āA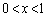 �Ȃ�A
�Ȃ�A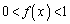 �ł��B
�ł��B
(2) 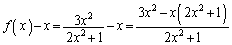
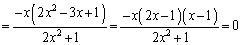 �@����@
�@����@���A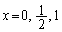 ......[��]
......[��]
(3) �E��}�ōl����킩��Ǝv���܂����A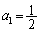 �̏ꍇ�́A������
�̏ꍇ�́A������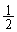 �̂܂܂Ȃ̂ŋɌ��l��
�̂܂܂Ȃ̂ŋɌ��l��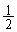 �ɂȂ�A
�ɂȂ�A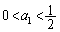 �̏ꍇ�̓O���t������_�̕��ɋ߂Â��ċɌ��l0�C
�̏ꍇ�̓O���t������_�̕��ɋ߂Â��ċɌ��l0�C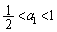 �̏ꍇ�̓O���t���
�̏ꍇ�̓O���t���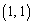 �̕��ɋ߂Â��ċɌ��l1�Ƃ������ƂɂȂ肻���ł��B���L�̂悤�Ȃ��Ƃ��v�����Ȃ��Ƃ��ł��A�O���t��`���Ă�������������Ă����A�������炢�͓_�������炦��Ǝv���܂��B
�̕��ɋ߂Â��ċɌ��l1�Ƃ������ƂɂȂ肻���ł��B���L�̂悤�Ȃ��Ƃ��v�����Ȃ��Ƃ��ł��A�O���t��`���Ă�������������Ă����A�������炢�͓_�������炦��Ǝv���܂��B ���ϒl�̒藝���g���Ȃ��̂ŁA�Ɍ��l��p�Ƃ��āA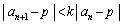 (
(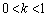 )�̌`����邽�߂ɁA�E��̃O���t�ŁA�_
)�̌`����邽�߂ɁA�E��̃O���t�ŁA�_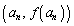 �Ɠ_
�Ɠ_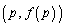 �����Ԓ����̌X��(���ϕω���)�ɒ��ڂ��܂��B���̖��ł́A�_
�����Ԓ����̌X��(���ϕω���)�ɒ��ڂ��܂��B���̖��ł́A�_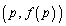 ��
��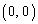 �C
�C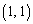 �Ƃ��čl���܂��B
�Ƃ��čl���܂��B
�}����킩��悤�ɁA���ϕω����F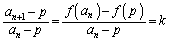 ��0��1�̊ԂɎ��܂肻���ł��B
��0��1�̊ԂɎ��܂肻���ł��B
(i) 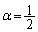 �̂Ƃ��A
�̂Ƃ��A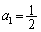 �C
�C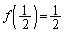 ���A2�ȏ�̂��ׂĂ̎��R��n�ɂ��āA
���A2�ȏ�̂��ׂĂ̎��R��n�ɂ��āA �ƂȂ�̂ŁA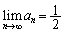
�@���A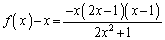
������A
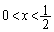 �̂Ƃ�
�̂Ƃ�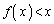 �@����A
�@����A
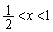 �̂Ƃ�
�̂Ƃ�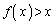 �@����B
�@����B
�ƂȂ�܂��B (ii) 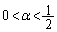 �̂Ƃ��A
�̂Ƃ��A 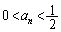 �Ɖ��肷��ƁA�A���A
�Ɖ��肷��ƁA�A���A�ƂȂ�̂ŁA���ׂĂ̎��R��n�ɂ���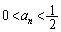 �ł��B�������A
�ł��B�������A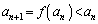 �ł��B
�ł��B
�]���āA���ׂĂ̎��R��n�ɂ��āA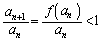 �ł��B
�ł��B
�����ł́A���ϕω���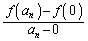 ���l���Ă��邱�Ƃɒ��ӂ��Ă��������B
���l���Ă��邱�Ƃɒ��ӂ��Ă��������B
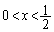 �ɂ����Ċ�
�ɂ����Ċ�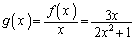 ���l����ƁA
���l����ƁA 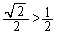 �Ȃ̂ŁA
�Ȃ̂ŁA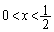 �ɂ����ẮA
�ɂ����ẮA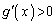 ���
���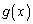 �͑������ł����āA
�͑������ł����āA������A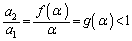
�܂��A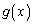 ���������ł��邱�Ƃ���A
���������ł��邱�Ƃ���A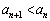 �ł���A
�ł���A �܂�A����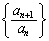 ��n����ƂƂ��Ɍ������鐔��ł��B
��n����ƂƂ��Ɍ������鐔��ł��B
������A���ׂĂ̎��R��n�ɂ��āA 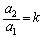 �Ƃ����ƁA
�Ƃ����ƁA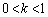 �ł����āA
�ł����āA
(iii) 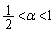 �̂Ƃ��A
�̂Ƃ��A 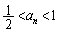 �Ɖ��肷��ƁA�B���A
�Ɖ��肷��ƁA�B���A�ƂȂ�̂ŁA���ׂĂ̎��R��n�ɂ���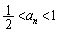 �ł��B�������A
�ł��B�������A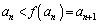 �ł��B
�ł��B
���x�́A���ϕω���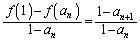 ���l���܂��B
���l���܂��B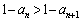 �Ȃ̂ŁA
�Ȃ̂ŁA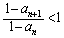 �ł��B
�ł��B
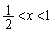 �ɂ����Ċ�
�ɂ����Ċ�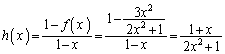 ���l����ƁA
���l����ƁA 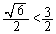 �C
�C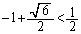 �Ȃ̂ŁA
�Ȃ̂ŁA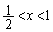 �ɂ�����
�ɂ�����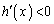 ���
���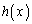 �͌������ł����āA
�͌������ł����āA������A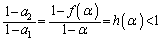
�܂��A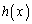 ���������ł��邱�Ƃ���A
���������ł��邱�Ƃ���A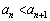 �ł���A
�ł���A �܂�A����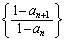 �́An����ƂƂ��Ɍ������鐔��ł��B
�́An����ƂƂ��Ɍ������鐔��ł��B
������A���ׂĂ̎��R��n�ɂ��āA 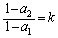 �Ƃ����ƁA
�Ƃ����ƁA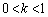 �ł����āA
�ł����āA�� 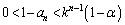 ������
������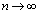 �Ƃ���ƁA
�Ƃ���ƁA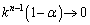 �Ƃ͂��݂����̌������A
�Ƃ͂��݂����̌������A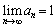
(i)�C(ii)�C(iii)���A
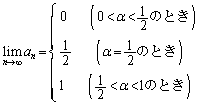 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 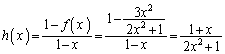 ���l����ƁA
���l����ƁA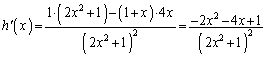
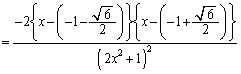
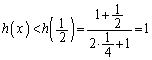
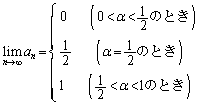 ......[��]
......[��]