�����㐔�w'08�N[2]
���W���ʂɂ����āA���_O�𒆐S�Ƃ��锼�a1�̉~C��ɓ_P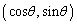 ���Ƃ�AP�ɂ�����C�̐ڐ�l�ƒ���
���Ƃ�AP�ɂ�����C�̐ڐ�l�ƒ���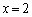 �̌�_��Q�Ƃ����B�������A
�̌�_��Q�Ƃ����B�������A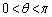 �Ƃ���Bl��̓_R��
�Ƃ���Bl��̓_R��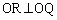 �����Ƃ��A�ȉ��̖₢�ɓ�����B
�����Ƃ��A�ȉ��̖₢�ɓ�����B
(1) R�̍��W��θ ��p���ĕ\���B
(2) θ ��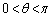 �͈̔͂��Ƃ��A����PR�̒����̍ő�l�Ƃ��̂Ƃ���θ �̒l�����߂�B
�͈̔͂��Ƃ��A����PR�̒����̍ő�l�Ƃ��̂Ƃ���θ �̒l�����߂�B (3) θ ��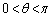 �͈̔͂��Ƃ���R�̋O�Ղ����߁A���̊T�`��`���B
�͈̔͂��Ƃ���R�̋O�Ղ����߁A���̊T�`��`���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�ŋ��߂�R�̍��W�̌`���悭�Ȃ��̂ŁA(3)�������Y�ނ����m��܂���B(2)�̌��ʂ���O�Ղ̊T�`�����߂�̂ŁA�������璅�z���邱�ƂɂȂ�܂��B
(1) ���_O�𒆐S�Ƃ��锼�a1�̉~C�F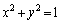
P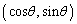 �ɂ������~C�̐ڐ�l�F
�ɂ������~C�̐ڐ�l�F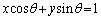 �@����@
�@����@
�@�ɂ�����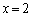 �Ƃ���ƁA
�Ƃ���ƁA
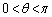 �ł�
�ł� ���A
���A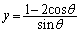
����āAQ�̍��W��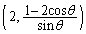 R�̍��W��
R�̍��W��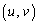 �Ƃ���ƁAR�͐ڐ�l��̓_�Ȃ̂ŁA�@���݂����܂��B����āA
�Ƃ���ƁAR�͐ڐ�l��̓_�Ȃ̂ŁA�@���݂����܂��B����āA  �@����A
�@����A ���A
���A�A�ɑ�����āA
�� 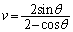 �B���A
�B���A ����āAR�̍��W��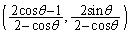 ......[��]
......[��]
(2) 
 �Ƃ���ƁA
�Ƃ���ƁA �C
�C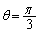 �C
�C �����\���(���̑������Q��)�A
�����\���(���̑������Q��)�A �̂Ƃ��A�ő�l�F
�̂Ƃ��A�ő�l�F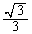 ......[��]
......[��]
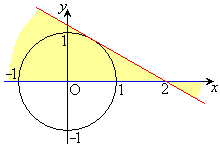 [�ʉ�]�@�~C��̓_
[�ʉ�]�@�~C��̓_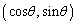 (
(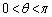 )�ɑ��āA
)�ɑ��āA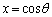 �C
�C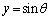 �C
�C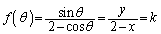 �Ƃ����ƁA
�Ƃ����ƁA ��ʂ钼��
��ʂ钼��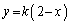 (�X���F
(�X���F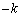 )���~C��
)���~C��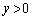 �̕����ƂƋ��L�_��L��������́A
�̕����ƂƋ��L�_��L��������́A (�~�ƒ����̈ʒu�W���Q��)�B������
(�~�ƒ����̈ʒu�W���Q��)�B������ �̍ő�l
�̍ő�l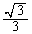 �����߂邱�Ƃ��ł��܂�(�E�}�̂悤�Ȑ}��`���čl���Ă��������B�}����
�����߂邱�Ƃ��ł��܂�(�E�}�̂悤�Ȑ}��`���čl���Ă��������B�}����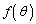 ���ő�Ƃ���θ �̒l�F
���ő�Ƃ���θ �̒l�F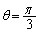 ���킩��܂�)�B
���킩��܂�)�B
(3) (1)���AR�̍��W��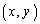 �Ƃ��āA
�Ƃ��āA �ƂȂ�̂ł����A�悭����}��ϐ��\���A�Ƃ����킯�ł͂Ȃ��̂ŁA�ǂ������Ȑ��ɂȂ�̂��A���ꂾ���ł͌��������܂���B
 �̂Ƃ��A
�̂Ƃ��A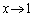 �C
�C �ł��B
�ł��B
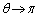 �̂Ƃ��A
�̂Ƃ��A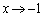 �C
�C �ł��BR��y���W�́A(2)�ɏo�Ă���
�ł��BR��y���W�́A(2)�ɏo�Ă��� ��2�{�ɂȂ��Ă���̂ŁA
��2�{�ɂȂ��Ă���̂ŁA �Ɠ����ω������܂��B
�Ɠ����ω������܂��B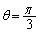 �̂Ƃ��A
�̂Ƃ��A �C
�C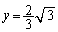 (
(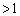 )�������AR�̋O�Ղ�y���W���ő�ƂȂ�Ƃ���ł��B�}��`���Ă݂��ȉ~�����m��Ȃ��ȁA�ƁA��������A�����Ȃ�A
)�������AR�̋O�Ղ�y���W���ő�ƂȂ�Ƃ���ł��B�}��`���Ă݂��ȉ~�����m��Ȃ��ȁA�ƁA��������A�����Ȃ�A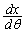 �C
�C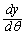 ((2)�Œ��ׂĂ��܂���)�C
((2)�Œ��ׂĂ��܂���)�C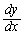 �ׂ�̂ł͂Ȃ��A
�ׂ�̂ł͂Ȃ��A ���ɍl����ׂ��ł��B
���ɍl����ׂ��ł��B
�C��1�����A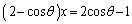 �C
�C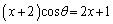 �C
�C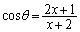
�C��2�����A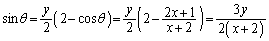
������āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
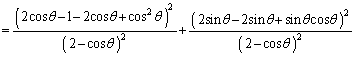
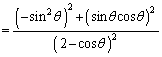
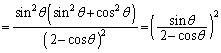


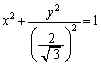
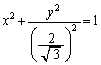 ��
��