�k�嗝�n���w'08�N�O��[5]
��
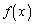 ��
��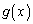 ��
��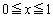 �͈̔͂Œ�`���ꂽ�A�����Ƃ���B
�͈̔͂Œ�`���ꂽ�A�����Ƃ���B
(1) 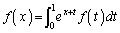 ����
����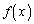 �͒萔��
�͒萔��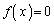 �݂̂ł��邱�Ƃ������B
�݂̂ł��邱�Ƃ������B (2) 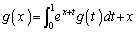 ����
����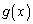 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ϕ��������ƌĂ��^�C�v�̖��ł��B
(1) ��[�Ɖ��[���萔�̒�ϕ��̒l�͒萔�ɂȂ�͂��ł����A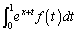 ��萔�Ƃ������Ƃ͂ł��܂���B�Ȃ��Ȃ�Ax���ω������
��萔�Ƃ������Ƃ͂ł��܂���B�Ȃ��Ȃ�Ax���ω������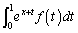 �̒l�͕ω����Ă��܂��萔�ł͂Ȃ�����ł��B��ϕ����̒���
�̒l�͕ω����Ă��܂��萔�ł͂Ȃ�����ł��B��ϕ����̒���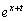 ��
��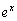 ���ϕ��̍ۂɎז��ɂȂ�܂��B
���ϕ��̍ۂɎז��ɂȂ�܂��B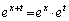 �ŁAt�Őϕ�����ۂ�t���ω����Ă�
�ŁAt�Őϕ�����ۂ�t���ω����Ă�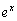 �͕ω����Ȃ��̂ŁA
�͕ω����Ȃ��̂ŁA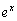 ��萔�Ƃ��Đϕ��̊O�ɒǂ��o���܂��B
��萔�Ƃ��Đϕ��̊O�ɒǂ��o���܂��B 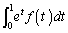 �͒萔�ɂȂ�̂ŁA�����A�Ƃ����A
�͒萔�ɂȂ�̂ŁA�����A�Ƃ����A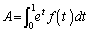 �@����@
�@����@������A
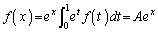 �@����A
�@����A������@�ɑ������ƁA
(2) (1)�Ɠ��l�ɂ��āA
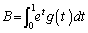 �@����B
�@����B�Ƃ����ƁA
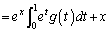
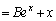 �@����C
�@����C������B�ɑ������ƁA
�����ŁA
���A
�� 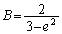 �C���A
�C���A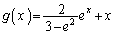 ......[��]
......[��]
�NjL�D�ϕ��������ɂ͂��낢��ȃ^�C�v������܂��B
��ϕ��̏�[�����[���萔�̏ꍇ�ɂ́A��L�ɂ悤�ɁA��ϕ����ɒu��������ƁA���m�̊��̌`�����܂�A��ϕ������s�ł���悤�ɂȂ�܂��B
��[�A���[���ϐ��ɂȂ��Ă�����A�Ⴆ�A
�啪��H'07�N[4]�F
a�𐳂̒萔�Ƃ���B��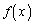 ��
��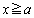 ��
�� �����B�������A�ΐ��͎��R�ΐ��Ƃ���B
(1) 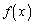 �����߂�B
�����߂�B (2) a�̒l�����߂�B
���̖��ł́A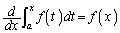 (��ϕ��̔������Q��)���g���܂��B
(��ϕ��̔������Q��)���g���܂��B
(2)�ł́A��ϕ���0�ɂ���悤�ɁA��[��x�����[��a�Ɉ�v�����܂��B
(1) 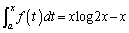 �@����@
�@����@
�@�̗��ӂ�x�Ŕ�������ƁA
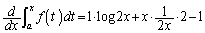 �@(�ς̔����@���Q��)
�@(�ς̔����@���Q��)
�� 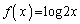 ......[��]
......[��]
(2) �@�ɂ����āA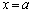 �Ƃ���ƁA
�Ƃ���ƁA
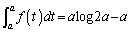
�� 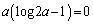
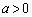 ���
���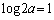 �C
�C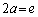
�� 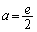 ......[��]
......[��]
�k��̖{��ł́A��ϕ����̒���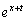 ��
��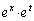 �Ƃ��邱�Ƃɂ���āA�ȒP�ɐϕ��̊O�ɒǂ��o�����Ƃ��ł��܂������A�ȒP�ɂ͒ǂ��o���Ȃ��^�C�v�̖�肪����܂��B�Ⴆ�A
�Ƃ��邱�Ƃɂ���āA�ȒP�ɐϕ��̊O�ɒǂ��o�����Ƃ��ł��܂������A�ȒP�ɂ͒ǂ��o���Ȃ��^�C�v�̖�肪����܂��B�Ⴆ�A
�{�鋳���'06[5]�F
���̊e��ɓ�����B
(1) �u���ϕ��@��p���āA�s��ϕ�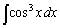 �����߂�B
�����߂�B (2) ���̓���������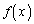 �����߂�B
�����߂�B
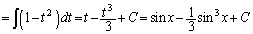 (C�F�ϕ��萔) ......[��]�@(�u���ϕ����Q��)
(C�F�ϕ��萔) ......[��]�@(�u���ϕ����Q��)(2) ��ϕ����̒���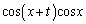 ��x���ϕ��̎ז��ɂȂ�܂��B����x�͊ȒP�ɂ͐ϕ��̊O�ɏo�čs���Ă���܂���B���@�藝���g���܂��B
��x���ϕ��̎ז��ɂȂ�܂��B����x�͊ȒP�ɂ͐ϕ��̊O�ɏo�čs���Ă���܂���B���@�藝���g���܂��B �����x��ϕ��̊O�ɒǂ��o�����Ƃ��ł��܂����B
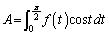 �@����@�C
�@����@�C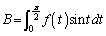 �@����A�Ƃ����ƁA
�@����A�Ƃ����ƁA �B���@�ɑ������ƁA
�����ŁA
��2���̐ϕ��́A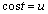 �Ƃ����ƁA
�Ƃ����ƁA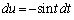 �Ct�F
�Ct�F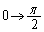 �̂Ƃ��Au�F
�̂Ƃ��Au�F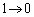
����āA
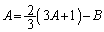 �C
�C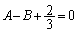 �@����D
�@����D�B���A�ɑ������ƁA
��1���̐ϕ��͇C���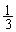
��2���̐ϕ��́A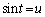 �Ƃ����ƁA
�Ƃ����ƁA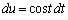 �Ct�F
�Ct�F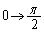 �̂Ƃ��Au�F
�̂Ƃ��Au�F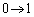
����āA
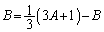 �C
�C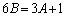 �@����E
�@����E�D�C�E��A������ƁA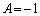 �C
�C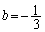
�B���A 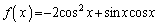 ......[��]
......[��]
����ɁA��ϕ����ɎO�p��������A��[�A���[�ɕϐ�������^�C�v������܂��B
�������ȑ嗝'98[3]�F
x�̊�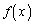 �C
�C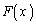 ���A�W
���A�W �����Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) �����̉��@�藝��p���A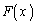 �̑�2������
�̑�2������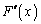 ��
��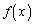 ��
��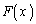 �ŕ\���B
�ŕ\���B (2) 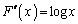 �Ƃ��āA
�Ƃ��āA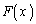 �����߂�B
�����߂�B (3) (2)�̏ꍇ�ɂ���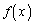 �����߂�B
�����߂�B
 �@����@
�@����@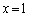 �Ƃ��܂��B
�Ƃ��܂��B
(1) �܂��A���@�藝��p���āA��ϕ����̒���x��ϕ��̊O�ɒǂ��o���܂��B 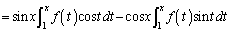 �@����A
�@����Ax���ϕ��̊O�ɏo���̂ŁA���ӂ�x�Ŕ������܂��B
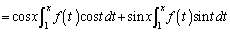 �@����B
�@����B�����x�Ŕ�������ƁA
���J�b�R���͇A���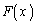 �ł��B����āA
�ł��B����āA 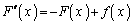 ......[��]
......[��](2) 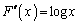
x�Őϕ����āA
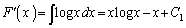 �@����C
�@����C�B�ɂ����āA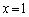 �Ƃ���ƁA��ϕ���0�ƂȂ�A
�Ƃ���ƁA��ϕ���0�ƂȂ�A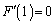
�C��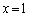 �Ƃ��āA
�Ƃ��āA �� 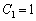 ��
�� 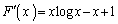
x�Őϕ����āA �A�ɂ����āA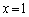 �Ƃ���ƁA��ϕ���0�ƂȂ�A
�Ƃ���ƁA��ϕ���0�ƂȂ�A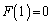
�D��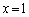 �Ƃ��āA
�Ƃ��āA �� 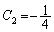 ��
�� 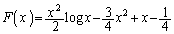 ......[��]
......[��] (3) (1)�̌��ʂ�p���āA
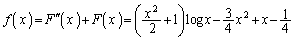 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B