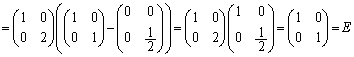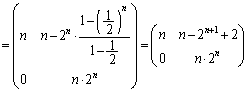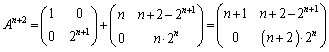�R�����w�����w'08�N[4]
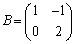 �C
�C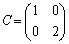 �Ƃ���B2���̐����s��
�Ƃ���B2���̐����s��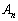 (
(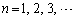 )��
)��
�����B�������AO�͗�s��Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) 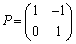 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A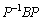 �����߂�B�܂��A
�����߂�B�܂��A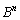 (
(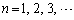 )�����߂�B
)�����߂�B
(2) 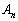 (
(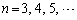 )��B�CC��p���ĕ\���B
)��B�CC��p���ĕ\���B
(3) 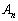 (
(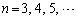 )�����߂�B
)�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����蕶�́A�u���߂Ȃ����v�u�\���Ȃ����v�Ƃ����\��(�l�I�ɂ͒�R���������ł�)�Ȃ̂ł����A�s���Ɨ��Ȃ��̂ŁA�������炵���u���w���v�̌������ɉ��߂܂����B
���āA���̖��́A(1)���s��̑Ίp���ɂ�����s��̗ݏ������߂�悭������ł����A(2)(3)�́A�s���3���ԑQ�����̖��ł��B�s��ł́A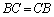 �ƌ����Ȃ��̂ŁA���l�̏ꍇ��3���ԑQ�����Ɠ����悤�ɂ͍s���܂���B�s��̑Q���������N�x�̓����ŗ��s����\��������ɓ���āA�s��ł͐��l�Ƃǂ��Ⴄ�̂��A�l���Ă݂����Ǝv���܂��B
�ƌ����Ȃ��̂ŁA���l�̏ꍇ��3���ԑQ�����Ɠ����悤�ɂ͍s���܂���B�s��̑Q���������N�x�̓����ŗ��s����\��������ɓ���āA�s��ł͐��l�Ƃǂ��Ⴄ�̂��A�l���Ă݂����Ǝv���܂��B
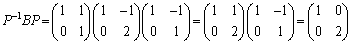 ......[��]
......[��]���ӂ�n�悷��ƁA
���A
������P�C�E����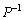 ��������ƁA
��������ƁA 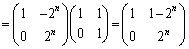 ......[��]
......[��]
(2) ��蕶���̑Q�����́A����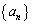 ���A3���ԑQ�����F
���A3���ԑQ�����F �����̂ł���A
��2�ʂ�����䐔���̌`������Ĉ�ʍ�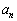 �����߂܂��B
�����߂܂��B
�������A�s��̗���������̖��ł́A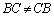 �ƂȂ�̂ŁA���䐔��̌`��2�ʂ��邱�Ƃ��ł��܂���B
�ƂȂ�̂ŁA���䐔��̌`��2�ʂ��邱�Ƃ��ł��܂���B
�ł����A1�ʂ�ł���A���䐔��̌`����邱�Ƃ��ł��܂��B
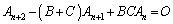
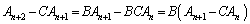 �@����@
�@����@���D��L�̂悤��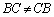 �Ȃ̂ŁA
�Ȃ̂ŁA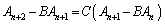 �͐��藧���܂���B
�͐��藧���܂���B
�@���J��Ԃ��Ďg�����Ƃɂ��A 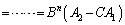 �@����A
�@����A2���̒P�ʍs���E�Ƃ��āA
����āA�A���A
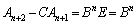 �@����B
�@����B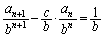 �@����C
�@����C
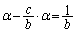 �@����D
�@����D�C�|�D�Ƃ��āA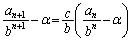
����œ��䐔��̌`����邱�Ƃ��ł��܂����A�B�ł́A�s��Ɋ���Z���Ȃ��̂ŁA����Ɠ����悤�ɂ͍s���܂���B
�����ŁA�K�������̘a�����߂���@�����p���āA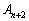 �ȊO�̍�����������Ă��܂��悤�ɂ��܂��B
�ȊO�̍�����������Ă��܂��悤�ɂ��܂��B 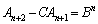
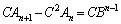 �@(�B��
�@(�B��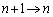 �Ƃ������̍�����C��������)
�Ƃ������̍�����C��������)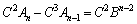 �@(�B��
�@(�B��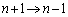 �Ƃ������̍�����
�Ƃ������̍�����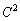 ��������)
��������)������
�ӁX�������킹��ƁA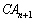 �C
�C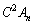 �C����C
�C����C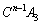 �������āA
�������āA 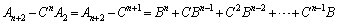 �@����E
�@����E�� 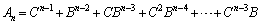 ......[��]
......[��]
(3) �E�̉E�ӂɏo�Ă��鍀�́A(1)�̌��ʂ��g���āA
���A
������A�E����A
�� 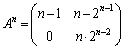 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 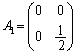 �C
�C