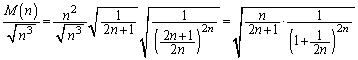奈良県立医大数学'09年[4]

奈良県立医大数学'09年[4]

(1) 任意の正整数nに対して関数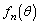

は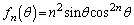

で定義されているものとする。このとき、

が成り立つかどうか調べよ。

(2) 各正整数nに対して、θ が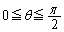

の範囲を動くときの関数

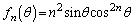の最大値を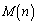

とおく。このとき、極限値

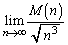を求めよ。

ただし、aを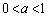

の範囲にある定数とするとき、

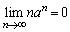であることは証明なしに用いてよい。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

解答　(1)は、

記号と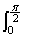

記号が交換可能かどうかという問題です。
(2)は、(1)の被積分関数の最大値が、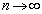

のとき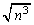

の定数倍に近づくように変化することを意味しています。

(1)

とおくと、

，θ：

のとき、t：

(置換積分を参照)

のとき、

　(数列の極限を参照)

のとき

より、

のとき

以上より、

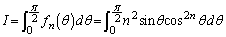
よって、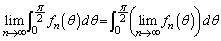

は成り立ちません。 ......[答]

(2)

　(積の微分法、合成関数の微分法、微分の公式を参照)

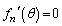とすると、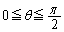

においては、

(

)

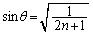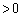各正整数nに対して、これを満たすθ がただ1つ存在し、それをαとすると、

，

0
	＋	0	－
0

増減表(関数の増減を参照)より、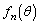

は、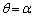

において最大値

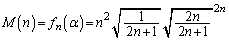をとります。

のとき、

より(極限の公式を参照)、

∴

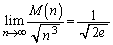......[答]

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。