��嗝�n���w'09�N���[4]
a�Cb�Cc�������Ƃ���B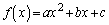 �C
�C �Ƃ����B2�̊�
�Ƃ����B2�̊�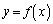 �C
�C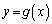 �̃O���t���قȂ�2�_P�CQ�����L���Ă���B����ɓ_P�ł�2�̃O���t�̐ڐ�����v���A�_Q�ł�2�̃O���t�̐ڐ��͒������Ă���Ƃ���B�����̏��������悤��a�Cb�Cc��ω�������Ƃ��A2�̃O���t�ň͂܂ꂽ�����̖ʐ�S�̍ŏ��l�����߂�B
�̃O���t���قȂ�2�_P�CQ�����L���Ă���B����ɓ_P�ł�2�̃O���t�̐ڐ�����v���A�_Q�ł�2�̃O���t�̐ڐ��͒������Ă���Ƃ���B�����̏��������悤��a�Cb�Cc��ω�������Ƃ��A2�̃O���t�ň͂܂ꂽ�����̖ʐ�S�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʐόv�Z�́A��ϕ��̌����F �𗘗p���܂��B
�𗘗p���܂��B
�_P�CQ��x���W��p�Cq�Ƃ��܂��B
�_P�ł�2�̃O���t���ڐ�����v����̂ŁA�_P��2�Ȑ��͐ڂ��܂��B�܂��A�_Q��2�Ȑ��������̂ŁA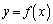 ��
��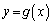 ��A������ƁA�d��
��A������ƁA�d�� �C��
�C��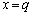 �������܂��B����āA
�������܂��B����āA
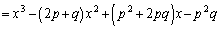 �@����@
�@����@
�@��p���āA2�̃O���t�ň͂܂ꂽ�������ʐ�S�́A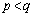 �C
�C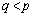 �C������̏ꍇ�����肤�邱�ƂƁA
�C������̏ꍇ�����肤�邱�ƂƁA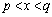 �C���邢�́A
�C���邢�́A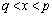 �ɂ����āA
�ɂ����āA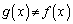 �ł��邱�Ƃɒ��ӂ��āA
�ł��邱�Ƃɒ��ӂ��āA
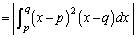
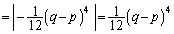 �@����B
�@����B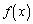 �C
�C ����������ƁA
����������ƁA
 �C
�C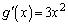
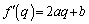 �C
�C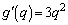
�A���A
�����ŁA�B�����Ă����S��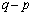 �ŕ\�����̂ŁA
�ŕ\�����̂ŁA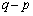 ���o�Ă���悤�Ɏ��ό`���܂��B
���o�Ă���悤�Ɏ��ό`���܂��B
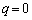 �̂Ƃ��A
�̂Ƃ��A ���A�Ȑ�
���A�Ȑ� �̐ڐ��̌X����0�ł����A2����
�̐ڐ��̌X����0�ł����A2����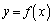 �̃O���t�̐ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��̂ŁA��ӂ��A
�̃O���t�̐ڐ���x���ɐ����ɂȂ邱�Ƃ͂Ȃ��̂ŁA��ӂ��A �ł��B����āA
�ł��B����āA
�B�ɑ������ƁA�������ρE���敽�ς̊W���A
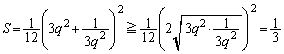 �@(�s�����̓���������
�@(�s�����̓��������� �C�܂�A
�C�܂�A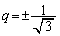 �̂Ƃ�)
�̂Ƃ�)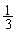 ......[��]
......[��]
�NjL�D����(x�̑������ŕ\������) �C
�C �̃O���t��
�̃O���t��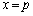 �ɂ�����ڐ�����v����Ƃ��ɁA�������F
�ɂ�����ڐ�����v����Ƃ��ɁA�������F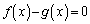 ��
��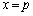 ���d���ɂ����Ƃ������Ă����܂��B
���d���ɂ����Ƃ������Ă����܂��B
�܂��A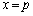 �ɂ�����ڐ�����v���邱�Ƃ���A
�ɂ�����ڐ�����v���邱�Ƃ���A
 �@(�X������v����)�@����C
�@(�X������v����)�@����C
 �@(�ړ_��y���W����v����)�@����D
�@(�ړ_��y���W����v����)�@����D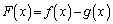 ��x�̑������ŕ\�������ŁA
��x�̑������ŕ\�������ŁA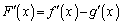 �ł��B
�ł��B
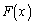 ��
��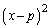 �Ŋ������]��(x��1�����A���邢�́A�萔)��
�Ŋ������]��(x��1�����A���邢�́A�萔)�� (C�CD�͒萔)�C����
(C�CD�͒萔)�C���� �Ƃ���ƁA
�Ƃ���ƁA
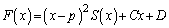 �@����E
�@����E
�C���A
����āA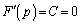
�E���A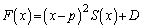
�D���A
����āA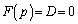
�]���āA ��
��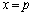 ���d���ɂ����܂��B
���d���ɂ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 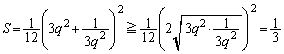 �@(�s�����̓���������
�@(�s�����̓���������