��嗝�n���w'09�N[3]
�Ȑ�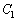 �F
�F �̓_P
�̓_P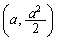 �ɂ�����@���Ɠ_Q
�ɂ�����@���Ɠ_Q �ɂ�����@���̌�_��R�Ƃ���B�������A
�ɂ�����@���̌�_��R�Ƃ���B�������A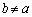 �Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) b��a�Ɍ���Ȃ��߂Â��Ƃ��AR�͂���_A�Ɍ���Ȃ��߂Â��BA�̍��W��a�ŕ\���B
(2) �_P���Ȑ� ����Ƃ��A(1)�ŋ��߂��_A���`���O�Ղ�
����Ƃ��A(1)�ŋ��߂��_A���`���O�Ղ�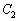 �Ƃ���B�Ȑ�
�Ƃ���B�Ȑ�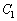 �ƋO��
�ƋO��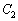 �̊T�`��`���A
�̊T�`��`���A ��
�� �̌�_�̍��W�����߂�B
�̌�_�̍��W�����߂�B (3) �Ȑ� �ƋO��
�ƋO��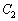 �ň͂܂ꂽ�����̖ʐς����߂�B
�ň͂܂ꂽ�����̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�Ȃ���ς̌v�Z���ł����A�w�i������܂��B
�Ȑ� �F
�F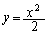
(1) �E �̂Ƃ��A�_P
�̂Ƃ��A�_P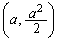 �ɂ������ڐ��̌X����a�C�@���̌X����
�ɂ������ڐ��̌X����a�C�@���̌X����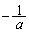 �ł��B�@���̕������́A
�ł��B�@���̕������́A �������āA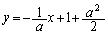 �@����@
�@����@
���l�ɁA�_Q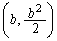 �ɂ�����@���̕������́A
�ɂ�����@���̕������́A 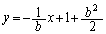 �@����A
�@����A�@�C�A��A������ƁA
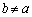 ���AR��x���W�́A
���AR��x���W�́A �@����B
�@����B�@���AR��y���W�́A
 �@����C
�@����C�E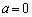 �̂Ƃ��A�_P
�̂Ƃ��A�_P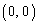 �ɂ�����@���́A
�ɂ�����@���́A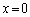 �C�]���āAR��x���W��0
�C�]���āAR��x���W��0 �A�ɂ�����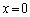 �Ƃ���ƁAR��y���W�́A
�Ƃ���ƁAR��y���W�́A
�B�� �Ƃ���ƁA
�Ƃ���ƁA
�C��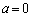 �Ƃ���ƁA
�Ƃ���ƁA
�]���āA�B�C�C�́A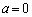 �̏ꍇ�ł����藧���܂��B
�̏ꍇ�ł����藧���܂��B b��a�Ɍ���ɂȂ��߂Â��Ƃ��A
����āAA ......[��]
......[��]
a����������ƁA
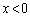 �ɂ����āAy��x�̌�����(���̑������Q��)�B
�ɂ����āAy��x�̌�����(���̑������Q��)�B
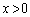 �ɂ����āAy��x�̑������B
�ɂ����āAy��x�̑������B
�܂��A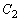 �͏�ɓʂȋȐ�(���̉������Q��)�B
�͏�ɓʂȋȐ�(���̉������Q��)�B
 �̂Ƃ��A
�̂Ƃ��A �C
�C
 �̂Ƃ�
�̂Ƃ� �C
�C �̂Ƃ�
�̂Ƃ�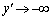 (���D������A
(���D������A ��
�� �Ő���Ă��邱�Ƃ��킩��܂��B������_(����Ă�)�ƌ����܂�)�C
�Ő���Ă��邱�Ƃ��킩��܂��B������_(����Ă�)�ƌ����܂�)�C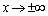 �̂Ƃ�
�̂Ƃ�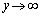
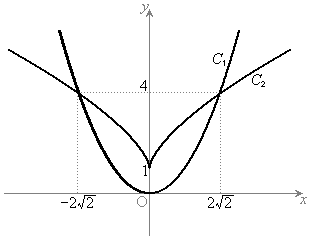
�Ȑ�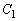 �ƋO��
�ƋO��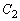 �̊T�`�͉E�}�B
�̊T�`�͉E�}�B
 �ɇD��������ƁA
�ɇD��������ƁA�� 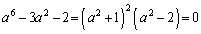
�D���A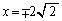 �C
�C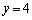
 ��
��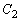 �̌�_�́A
�̌�_�́A ......[��]
......[��]
(3) �D���a����������ƁA
���߂��ʐ�S�́Ay���Ɋւ���Ώ̐����l�����āA 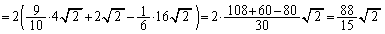 ......[��]
......[��]
�NjL�D
�{��̗ޑ�Ƃ��Ď��̖�肪�������܂��B�h�q���'95�N[4]�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� ��
��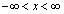 ��
�� �C
�C ���݂����Ă���B�Ȑ�
���݂����Ă���B�Ȑ�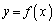 ��̑��قȂ�2�_��P
��̑��قȂ�2�_��P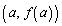 �CQ
�CQ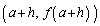 �Ƃ��Ĉȉ��̖₢�ɓ�����B
�Ƃ��Ĉȉ��̖₢�ɓ�����B
(1) 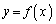 �̓_P�ɂ�����@���Ɠ_Q�ɂ�����@���̌�_R�̍��W�����߂�B
�̓_P�ɂ�����@���Ɠ_Q�ɂ�����@���̌�_R�̍��W�����߂�B
(2)  �̂Ƃ��A����PR�̒����̋Ɍ��l�����߂�B
�̂Ƃ��A����PR�̒����̋Ɍ��l�����߂�B
(3) 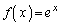 �̂Ƃ��A(2)�̋Ɍ��l���ŏ��ɂ���a�̒l�����߂�B
�̂Ƃ��A(2)�̋Ɍ��l���ŏ��ɂ���a�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Ȃ�ʓ|�ł����A�{��Ɠ��l�ɑf���Ɍv�Z���Ă����܂��B
(1) �_P�ɂ�����@���́A
 �@����@
�@����@�_Q�ɂ�����@���́A
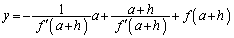 �@����A
�@����A�@�C�A��A�����āA
��_R��x���W�́A
 ......[��]
......[��]�@���A��_R��y���W�́A
 ......[��]
......[��]
(2)  �Ƃ���ƁA
�Ƃ���ƁA ���A
�� 
�� 
(3) (2)�̌��ʂŁA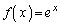 �Ƃ���ƁA
�Ƃ���ƁA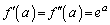 ���A
���A �Ƃ����ƁA
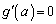 �Ƃ���ƁA
�Ƃ���ƁA ���A
���A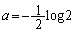 (���e)
(���e)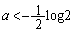 �ɂ�����
�ɂ�����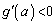 �C
�C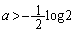 �ɂ�����
�ɂ�����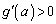 ���APR���ŏ��ɂ���a�́A
���APR���ŏ��ɂ���a�́A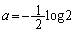 ......[��]
......[��]
���'09�N�O��[3]�̖{��́A���̖h�q���̖��ŁA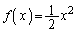 �Ƃ����ꍇ�ɂ�����܂��B
�Ƃ����ꍇ�ɂ�����܂��B
�Ȑ�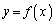 ��̓_
��̓_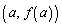 �ɂ����Ă��̋Ȑ��Ɛڂ���~�ł��̋Ȑ��̔����������ł��悭�ߎ�������̂��ȗ��~(���邢�́A�ڐG�~)�ƌ����܂����A���̖{��ŋ��߂�
�ɂ����Ă��̋Ȑ��Ɛڂ���~�ł��̋Ȑ��̔����������ł��悭�ߎ�������̂��ȗ��~(���邢�́A�ڐG�~)�ƌ����܂����A���̖{��ŋ��߂�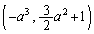 �͋ȗ��~�̒��S�ɂȂ��Ă��܂��B
�͋ȗ��~�̒��S�ɂȂ��Ă��܂��B
�h�q���̉̓r���ɏo�Ă����A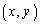 �̋Ɍ�
�̋Ɍ�
���A��ʓI�ȏꍇ�̋ȗ��~�̒��S�ł��B�Ȑ�������_�ɂ�����ȗ��~�̒��S���`���O��(���̖{��Ő}�������O��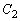 )���k���ƌ����܂��B
)���k���ƌ����܂��B
�h�q���̖��ŋ��߂Ă���PR�̋Ɍ�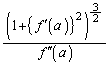 �́A�ȗ��~�̔��a�ɂȂ��Ă��āA�ȗ����a�ƌ����܂��B2005�N4���ɓ��s�œd�Ԃ��J�[�u���Ȃ��肫�ꂸ�ɒE�����}���V�����Ɍ��˂���A�Ƃ����߂����厖�̂��N���܂������A�ȗ����a�̓J�[�u�̋Ȃ������l�����ł̏d�v�ȗv�f�ł��B
�́A�ȗ��~�̔��a�ɂȂ��Ă��āA�ȗ����a�ƌ����܂��B2005�N4���ɓ��s�œd�Ԃ��J�[�u���Ȃ��肫�ꂸ�ɒE�����}���V�����Ɍ��˂���A�Ƃ����߂����厖�̂��N���܂������A�ȗ����a�̓J�[�u�̋Ȃ������l�����ł̏d�v�ȗv�f�ł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 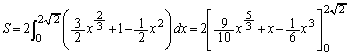
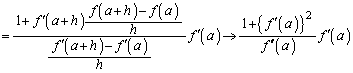

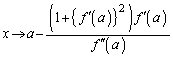


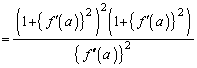

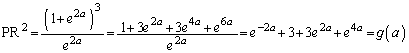
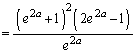
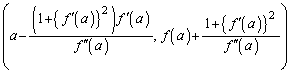
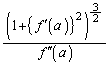 �́A�ȗ��~�̔��a�ɂȂ��Ă��āA�ȗ����a�ƌ����܂��B2005�N4���ɓ��s�œd�Ԃ��J�[�u���Ȃ��肫�ꂸ�ɒE�����}���V�����Ɍ��˂���A�Ƃ����߂����厖�̂��N���܂������A�ȗ����a�̓J�[�u�̋Ȃ������l�����ł̏d�v�ȗv�f�ł��B
�́A�ȗ��~�̔��a�ɂȂ��Ă��āA�ȗ����a�ƌ����܂��B2005�N4���ɓ��s�œd�Ԃ��J�[�u���Ȃ��肫�ꂸ�ɒE�����}���V�����Ɍ��˂���A�Ƃ����߂����厖�̂��N���܂������A�ȗ����a�̓J�[�u�̋Ȃ������l�����ł̏d�v�ȗv�f�ł��B