札幌医大数学'09年[3]
平面上に2点P
，Q
がある。ただしa，bは正の数とする。線分OPと線分OQ上に、それぞれ動点M，Nがあり、
を満たすように動くとき、線分MNが通過する領域をTとする。ここでOは原点を表す。
(1) 領域Tは線分OP，OQと、PとQを結ぶ曲線で囲まれる。この曲線の方程式を求めよ。
(2) 領域Tを図示せよ。
(3) 領域Tをx軸のまわりに1回転してできる立体をUとする。2点P，Qが単位円周上にあるとき、立体Uの体積を最大にするようなaの値と、そのときの立体Uの体積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 体積を除いて実質的に数学Ⅱの範囲の微積分の問題ですが、ポイントとなるところは、(1)で2次方程式の解の範囲を考える部分です。
(1)(2) A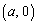
として、直線PAにMから下ろした垂線の足をHとします。 
であって、△OPAと△MPHは相似なので、MP：PH：HM = OP：PA：AO =
：b：a 
とすると、
，
これより、Mの座標は
Nの座標は
直線MNの傾きは、 rについて整理すると、
･･･①ここで、Mが線分OP上の点であることから、
･･･②であることに注意します。①の左辺を
とおくと、rの2次方程式
は、②の範囲に解をもちます。②の範囲の両端において、 となりますが、線分MN上の点
は、
の部分であって
かつ
の部分に存在するので、
，
を満たします。つまり、
，
です。従って、2次方程式
が②の範囲に解をもつための条件は、
の判別式Dと
のグラフの軸の位置
に関して(2次方程式の解の配置を参照)、 
･･･③
･･･④③と、
より、 ∴ 
･･･⑤
④より、
∴ 
線分MN上の点は
の部分に存在するので、求める領域Tは、 であって図示すると、右図黄緑色着色部分(境界線を含む)。
(1)のPとQを結ぶ曲線の方程式は、⑤の不等号を等号に変えて、
......[答] ･･･⑥
(3) Uは、底円の半径b，高さaの円錐から、曲線⑥と直線
に挟まれた部分を除いた図形になります。その体積Vは、 
(∵ ⑥)2点P，Qが単位円周上にあるとき、
より、
>
増減表より(3次関数の最大最小を参照)、立体Uの体積を最大にするaの値は、
......[答]
そのときの立体Uの体積は、
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
かつ 
かつ 
とすると、
においては
，このとき、
