�L���Z�ȑ吔�w'09�N[1]
��̐���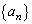 �C
�C �����̂悤�ɒ�`����Ă���B
�����̂悤�ɒ�`����Ă���B
�ȉ��̖₢�ɓ�����B
(1) ���� �̈�ʍ������߂�B
�̈�ʍ������߂�B (2) ���� �����䐔��ƂȂ�Ƃ��Ak�̒l�����߂�B�������A
�����䐔��ƂȂ�Ƃ��Ak�̒l�����߂�B�������A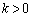 �Ƃ���B
�Ƃ���B (3) ��(2)�ŋ��߂�k�̒l��p���āA����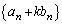 �̈�ʍ������߂�B
�̈�ʍ������߂�B (4) ��(1)�C(3)�̌��ʂ�p���āA����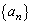 �����
����� �̈�ʍ������߂�B
�̈�ʍ������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�A���Q�����̊�{���ł��B�A���Q�����̎�v�ȉ�@�́A
��3�ʂ肠��܂��B�{��ł́A��@1�ʼn����悤�ɗU�������Ă��܂��B�Ō�ɁA�ʉ��Ƃ��āA��@2�C��@3�ł�����Ă݂܂��B
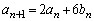 �@����@
�@����@
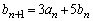 �@����A
�@����A
(1) �@�|�A���A
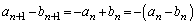 �@(
�@(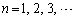 )
)����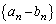 �́A�����F
�́A�����F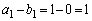 �C����F
�C����F �����䐔���ł��B
�����䐔���ł��B  ......[��]�@����B
......[��]�@����B
(2) �@�{�A�~k���A
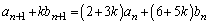 �@(
�@(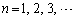 )
)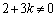 �Ƃ��āA
�Ƃ��āA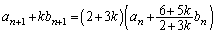 �@����C
�@����C�����ŁA �ł���A
�ł���A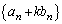 �͌���
�͌��� �̓��䐔��ɂȂ�܂��B
�̓��䐔��ɂȂ�܂��B 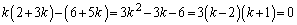 �@����D
�@����D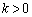 ���A
���A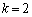 ......[��]���D�D��������
......[��]���D�D�������� �Ƃ������������܂����A
�Ƃ������������܂����A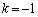 �̂Ƃ��ɂ́A(1)�̓��䐔��ɂȂ�܂��B����
�̂Ƃ��ɂ́A(1)�̓��䐔��ɂȂ�܂��B����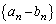 �����䐔��ɂȂ�Ƃ����q���g���Ȃ��Ă��A����
�����䐔��ɂȂ�Ƃ����q���g���Ȃ��Ă��A����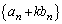 �����䐔��ɂȂ�悤��k�̒l���߂�A(1)�̓��䐔��̌`�������邱�Ƃɒ��ӂ��Ă��������B
�����䐔��ɂȂ�悤��k�̒l���߂�A(1)�̓��䐔��̌`�������邱�Ƃɒ��ӂ��Ă��������B
(3)  �̂Ƃ��A�C�́A
�̂Ƃ��A�C�́A ����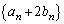 �́A�����F
�́A�����F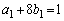 �C����F8�̓��䐔��ł��B
�C����F8�̓��䐔��ł��B 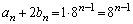 ......[��]�@����E
......[��]�@����E
(4) �B�~2�{�E���A
��  ......[��]�E�|�B���A
......[��]�E�|�B���A �� 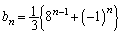 ......[��]
......[��]
�ʉ�1�D3���ԑQ�����Ɏ�������ʼn��Ă݂܂��B�܂��A�@�ɂ����āA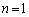 �Ƃ��āA
�Ƃ��āA  �C
�C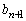 ���������邱�Ƃ��l���܂��B
���������邱�Ƃ��l���܂��B
�@��n�� �Ƃ��āA
�Ƃ��āA�A��������ƁA
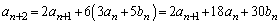 �@����F
�@����F�@���A
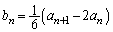 �@����G
�@����G�F�ɑ�����āA
�� 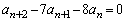 �@����H
�@����H
�����������F
��  �H ��
�H �� 
 �́A�����F
�́A�����F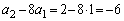 �C����F
�C����F �̓��䐔��ł��B
�̓��䐔��ł��B  �@����I
�@����I�H �� 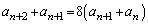
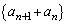 �́A�����F
�́A�����F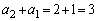 �C����F8�̓��䐔��ł��B
�C����F8�̓��䐔��ł��B 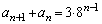 �@����J
�@����J�J�|�I���A
��  �G�ɑ�����āA
�G�ɑ�����āA
�ʉ�2�D�s��̗ݏ��𗘗p���Ă݂܂��B�@�C�A���s����g���ď����ƁA 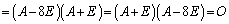 �@����K
�@����K������A�s��A���ŗL�l8�C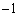 �������Ƃ��킩��܂��B����2�̌ŗL�l���g���āA
�������Ƃ��킩��܂��B����2�̌ŗL�l���g���āA ���݂����s��P�CQ�����߂�ƁA
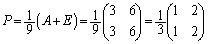 �@����L
�@����L
 �@����M
�@����M������p���āA
������A�L�C�M��p���āA
���D(2)�̇D���d�������ꍇ(���̂Ƃ��A3���ԑQ�����̓������������d���������܂��B�܂��A�K��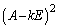 �̌`�ƂȂ�A�ŗL�l��1�����ɂȂ�܂�)�A�Ⴆ�A
�̌`�ƂȂ�A�ŗL�l��1�����ɂȂ�܂�)�A�Ⴆ�A
�̂悤�ȏꍇ�A�N�{�O�~k���A
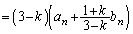 �@(
�@( )�@����P
)�@����P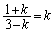 �̂Ƃ�
�̂Ƃ� �����䐔��ƂȂ�܂��B
�����䐔��ƂȂ�܂��B
�� 
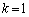 �̂Ƃ��A�P�́A
�̂Ƃ��A�P�́A
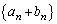 �́A�����F
�́A�����F �C����F2�̓��䐔��ł��B
�C����F2�̓��䐔��ł��B
���̂Ƃ��ɂ́A���䐔��̌`��2�ʂ��邱�Ƃ��ł��܂���B�N�ɂ����āA
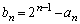 �@����Q
�@����Q
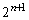 �Ŋ����āA
�Ŋ����āA
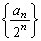 �́A�����F
�́A�����F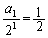 �C�����F
�C�����F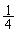 �̓�������ŁA
�̓�������ŁA
�� 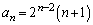
�Q���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B