�R����㐔�w'10�N[4]
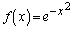 �Ƃ���B���̖₢�ɓ�����B
�Ƃ���B���̖₢�ɓ�����B
(1) ��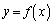 �̑����A�ɒl�A�O���t�̉��ʁA�ϋȓ_�A�Q�ߐ��ׁA�O���t�������B
�̑����A�ɒl�A�O���t�̉��ʁA�ϋȓ_�A�Q�ߐ��ׁA�O���t�������B (2) 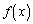 �̑�n��������
�̑�n��������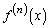 �Ƃ���B���̂Ƃ��A�C�ӂ̐��̊n�ɑ��āA
�Ƃ���B���̂Ƃ��A�C�ӂ̐��̊n�ɑ��āA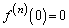 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (3) 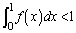 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (4) �C�ӂ̐��̎���a�ɑ��āA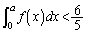 �ł��邱�Ƃ������B�������A�K�v�Ȃ��
�ł��邱�Ƃ������B�������A�K�v�Ȃ��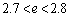 �ł��邱�Ƃ�p���Ă��悢�B
�ł��邱�Ƃ�p���Ă��悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ϕ��̒l�̕]���̖��ł����A(2)�C(4)�́A�l�����ނ����m��܂���B
(1) 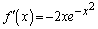
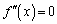 �Ƃ���ƁA
�Ƃ���ƁA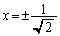
�ϋȓ_�́A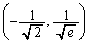 �C
�C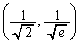 ......[��]
......[��]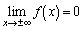 ���A�Q�ߐ���
���A�Q�ߐ���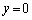 ......[��]�����\�́A�ȉ��̒ʂ�B
......[��]�����\�́A�ȉ��̒ʂ�B| x |
| 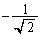 |
| 0 |
| 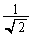 |
|
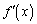 | �{ | �{ | �{ | 0 | �| | �| | �| |
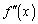 | �{ | 0 | �| | �| | �| | 0 | �{ |
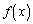 |  | 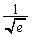 |  | 1 |  | 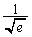 |  |
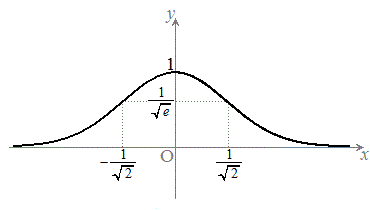 �O���t�͉E�}�B
�O���t�͉E�}�B
(2) (1)���A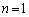 �̂Ƃ��A
�̂Ƃ��A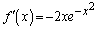 ���A
���A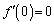 �ł��B
�ł��B 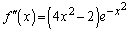 ���A
���A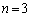 �̂Ƃ����A
�̂Ƃ����A���A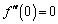 �ł��B
�ł��B
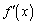 �C
�C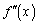 �C
�C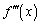 �����Ă���ƁA
�����Ă���ƁA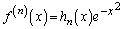 �̌`(�����̓������Q��)�ɂȂ��Ă��āAn�����̊�̎���
�̌`(�����̓������Q��)�ɂȂ��Ă��āAn�����̊�̎���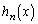 �͊���̍��݂̂̐����An�����̋����̂Ƃ���
�͊���̍��݂̂̐����An�����̋����̂Ƃ���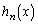 �͋������̍��݂̂̐����ƂȂ邱�Ƃ��\���ł��܂��B
�͋������̍��݂̂̐����ƂȂ邱�Ƃ��\���ł��܂��B ���D�����Ƃ����̂́A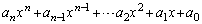 �Ƃ����������̌`�ɕ\������̂��Ƃł��B
�Ƃ����������̌`�ɕ\������̂��Ƃł��B 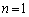 �̂Ƃ��A
�̂Ƃ��A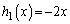
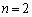 �̂Ƃ��A
�̂Ƃ��A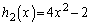
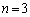 �̂Ƃ��A
�̂Ƃ��A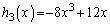
�ƂȂ��Ă��܂��Bm�����R�����Ƃ��āA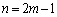 �̂Ƃ��A
�̂Ƃ��A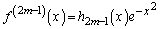 �C
�C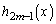 �͊���̍��݂̂̐����A�Ɖ��肵�܂��B
�͊���̍��݂̂̐����A�Ɖ��肵�܂��B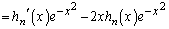
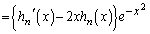 �@����@
�@����@����̍��̔����͋������̍��ƂȂ�A�������̍��̔����͊���̍��ƂȂ邱�Ƃɒ��ӂ��܂�(�����E�������Q��)�B
�@�ɂ����āA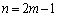 �Ƃ���ƁA����ɂ��A
�Ƃ���ƁA����ɂ��A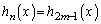 �͊���̍��݂̂̐����ł��B
�͊���̍��݂̂̐����ł��B
���J�b�R����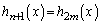 �Ƃ����ƁA
�Ƃ����ƁA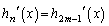 �͋������̍��݂̂̐����A
�͋������̍��݂̂̐����A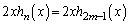 ���������̍��݂̂̐����Ȃ̂ŁA���J�b�R��
���������̍��݂̂̐����Ȃ̂ŁA���J�b�R��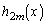 �͋������̍��݂̂̐����ɂȂ�܂��B
�͋������̍��݂̂̐����ɂȂ�܂��B
���l�ɁA�@�ɂ����āA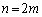 �Ƃ���ƁA
�Ƃ���ƁA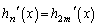 �͊���̍��݂̂̐����A
�͊���̍��݂̂̐����A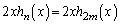 ������̍��݂̂̐����Ȃ̂ŁA���J�b�R����
������̍��݂̂̐����Ȃ̂ŁA���J�b�R����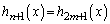 �Ƃ����āA����͊���̍��݂̂̐����ł��B
�Ƃ����āA����͊���̍��݂̂̐����ł��B
����āA�A�[�I�ɁA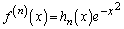 �Cn����̎���
�Cn����̎���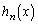 �͊���̍��݂̂̐����A�Ƃ������Ƃ������܂���(���w�I�A�[�@���Q��)�B
�͊���̍��݂̂̐����A�Ƃ������Ƃ������܂���(���w�I�A�[�@���Q��)�B
����āAn�����̊�̂Ƃ��A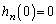 �Ȃ̂ŁA
�Ȃ̂ŁA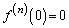 �ł��B
�ł��B �ʉ��D�ǂ�����Ďv�����̂��킩��܂��A�ȉ��̂悤�Ȑ▭�ȉ�@������܂��B
�������āA
����ɔ�������ƁA
������J��Ԃ��ƁA
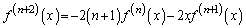 �@����A
�@����A�ƂȂ邱�Ƃ��\���ł��܂��B��������w�I�A�[�@�Ŏ����A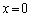 �������邱�Ƃɂ���Ă��A��ӂ������܂��B
�������邱�Ƃɂ���Ă��A��ӂ������܂��B
(3) (1)�̑����\���A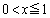 �ɂ����āA
�ɂ����āA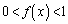 �ł��B
�ł��B �� 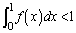
(4) (3)���A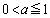 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A �͖��炩�ł��B
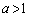 �̂Ƃ��A�Ȑ�
�̂Ƃ��A�Ȑ�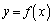 �͉��ɓʂȂ̂ŁA
�͉��ɓʂȂ̂ŁA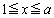 �ɂ����āA
�ɂ����āA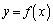 �̃O���t�́A���̗��[
�̃O���t�́A���̗��[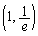 �C
�C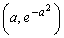 �����Ԑ������������ɗ��܂��B�]���āA
�����Ԑ������������ɗ��܂��B�]���āA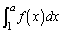 �́A
�́A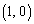 �C
�C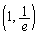 �C
�C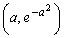 �C
�C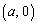 ��4���_�Ƃ����`�̖ʐ�S�����������Ȃ�܂��B
��4���_�Ƃ����`�̖ʐ�S�����������Ȃ�܂��B �Ƃ��낪�A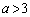 �̂Ƃ��A
�̂Ƃ��A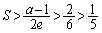 �ƂȂ��Ă��܂��̂ŁA
�ƂȂ��Ă��܂��̂ŁA ���������A(3)��p���Ă��A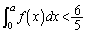 �Ƃł��܂���B
�Ƃł��܂���B
�]���āA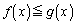 �ł����āA
�ł����āA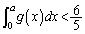 �ƂȂ�悤�ȁA�ʂ�
�ƂȂ�悤�ȁA�ʂ�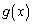 ��T�����ƂɂȂ�܂��B
��T�����ƂɂȂ�܂��B
���Z�͈̔͂ł�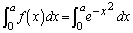 �̐ϕ��v�Z���s���Ȃ��̂ł����A
�̐ϕ��v�Z���s���Ȃ��̂ł����A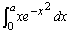 �ł���A�ϕ��v�Z�����s�ł��܂��B
�ł���A�ϕ��v�Z�����s�ł��܂��B
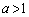 �̂Ƃ������l����悢�̂ŁA
�̂Ƃ������l����悢�̂ŁA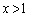 ���Ƃ���ƁA
���Ƃ���ƁA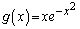 �Ƃ��āA
�Ƃ��āA �܂�A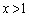 �ł����
�ł����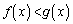 �ł��B
�ł��B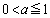 �̂Ƃ��ɂ�(3)�𗘗p���邱�Ƃɂ��āA���ӂ�
�̂Ƃ��ɂ�(3)�𗘗p���邱�Ƃɂ��āA���ӂ�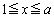 �ɂ����Đϕ�����ƁA
�ɂ����Đϕ�����ƁA �E�ӂ̐ϕ��́A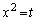 �Ƃ������Ƃɂ��A
�Ƃ������Ƃɂ��A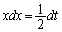 �Cx�F
�Cx�F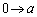 �̂Ƃ�t�F
�̂Ƃ�t�F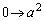 (�u���ϕ����Q��)
(�u���ϕ����Q��) �ȏ���A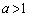 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A
�NjL�D���́A���̖��ɂ͔w�i������܂��B(2)�ɏo�Ă���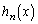 ��p���āA
��p���āA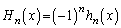 �ƕ\����鑽�������G���~�[�g�������ƌ����܂��B���̂Ƃ���
�ƕ\����鑽�������G���~�[�g�������ƌ����܂��B���̂Ƃ���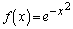 �����ƌ����܂��B
�����ƌ����܂��B
�ȂǂƂȂ�܂��B
�A�ƁA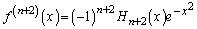 �@����B�C
�@����B�C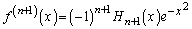 �@����C�C
�@����C�C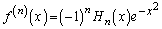 �Ƃ���A
�Ƃ���A
�� 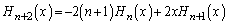 �@����D
�@����D
�C���ӂ��������ƁA
�B���A
�� 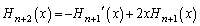 �@����E
�@����E
�D�Ɣ�r���āA
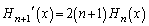 �@����F
�@����F
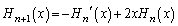 �@����G
�@����G
�F��p���āA
�� 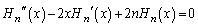 �@����H
�@����H
���ꂪ�A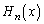 ���]�������������ł��B
���]�������������ł��B
��w�Ŋw�ԕ����̒��Łu�ʎq�͊w�v�Ƃ������삪����܂��B���̒��́u���a�U���q�v�̖��œo�ꂷ�������������ł��B(2)�̕ʉ��́A���������Ƃ��납�甭�z�������̂ł��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B