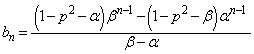�R����㐔�w'10�N[2]
�\���o��m����p�C�����o��m����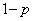 �ł���d�݂�n����B���̂Ƃ��A�d�݂�1���邲�ƂɁA�\�Ȃ��A���L�^���A���Ȃ��B���L�^���āA1��ڂ��珇�Ԃ�1��ɕ��ׂ�B�������An��2�ȏ�̐����ł���A
�ł���d�݂�n����B���̂Ƃ��A�d�݂�1���邲�ƂɁA�\�Ȃ��A���L�^���A���Ȃ��B���L�^���āA1��ڂ��珇�Ԃ�1��ɕ��ׂ�B�������An��2�ȏ�̐����ł���A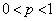 �Ƃ���B���̂悤�ɕ��ׂ�n�̕����̒���
�Ƃ���B���̂悤�ɕ��ׂ�n�̕����̒���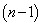 �g����A������2�������A�ǂ��AB�̏��Ԃɕ���ł��Ȃ��m����
�g����A������2�������A�ǂ��AB�̏��Ԃɕ���ł��Ȃ��m���� �Ƃ��A�ǂ��AA�̏��Ԃɕ���ł��Ȃ��m����
�Ƃ��A�ǂ��AA�̏��Ԃɕ���ł��Ȃ��m����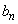 �Ƃ���B
�Ƃ���B
(1) 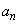 �����߂�B
�����߂�B (2) 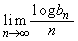 �����߂�B
�����߂�B (3)  �ƂȂ�悤��p�̒l�A����сA���̂Ƃ���
�ƂȂ�悤��p�̒l�A����сA���̂Ƃ���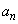 �C
�C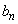 �����߂�B�������A
�����߂�B�������A �ƂȂ邱�Ƃ�p���Ă��悢�B
�ƂȂ邱�Ƃ�p���Ă��悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@ ��3���ԑQ�������������Ȃ��̂ŁA�Ɍ����Ƃ邠����ŕs���ɂȂ�܂����A�r�s���ŋ��s�˔j���邱�Ƃɂ��܂��B
��3���ԑQ�������������Ȃ��̂ŁA�Ɍ����Ƃ邠����ŕs���ɂȂ�܂����A�r�s���ŋ��s�˔j���邱�Ƃɂ��܂��B
(1) n�̕����̒���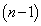 �g����A������2�������A�ǂ��AB�̏��Ԃɕ���ł��Ȃ��Ƃ��An�̕����̕��т̒���A���o�Ă���Ƃ��̎���A�łȂ���Ȃ�Ȃ��̂ŁA��xA���o�Ă���Ƃ��̌�͑S��A�ɂȂ�܂��B���̂悤�ɂȂ�̂́A�ȉ��̏ꍇ�ł��B
�g����A������2�������A�ǂ��AB�̏��Ԃɕ���ł��Ȃ��Ƃ��An�̕����̕��т̒���A���o�Ă���Ƃ��̎���A�łȂ���Ȃ�Ȃ��̂ŁA��xA���o�Ă���Ƃ��̌�͑S��A�ɂȂ�܂��B���̂悤�ɂȂ�̂́A�ȉ��̏ꍇ�ł��B n�̕����̕��т��ׂ�A�ƂȂ�ꍇ�A�����m����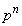 1�Ԗڂ�B��2�Ԗڈȍ~���ׂ�A�ƂȂ�ꍇ�A���̊m����
1�Ԗڂ�B��2�Ԗڈȍ~���ׂ�A�ƂȂ�ꍇ�A���̊m����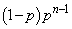 1�Ԗڂ�2�Ԗڂ�B��3�Ԗڈȍ~���ׂ�A�ƂȂ�ꍇ�A���̊m����
1�Ԗڂ�2�Ԗڂ�B��3�Ԗڈȍ~���ׂ�A�ƂȂ�ꍇ�A���̊m����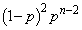
�@�E�E�E�E�E�En�̕����̕��т��ׂ�B�ƂȂ�ꍇ�A���̊m����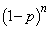
�ȏ�̏ꍇ�͂��ׂČ݂��ɔr���ŁA���߂�m�� �́A�ȏ�̊e�ꍇ�̊m���̘a�ƂȂ�A
�́A�ȏ�̊e�ꍇ�̊m���̘a�ƂȂ�A  �̂Ƃ��́A
�̂Ƃ��́A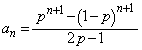
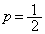 �̂Ƃ��́A
�̂Ƃ��́A
(2) 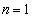 �̏��l����ƁA1�̕����̕��т̒���AA�̏��̕��т͌���Ȃ��̂ŁA
�̏��l����ƁA1�̕����̕��т̒���AA�̏��̕��т͌���Ȃ��̂ŁA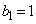 �ł��B
�ł��B 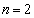 �̂Ƃ��A2�̕����̕��т̒���AA�̏��������m����
�̂Ƃ��A2�̕����̕��т̒���AA�̏��������m����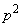 �ŁA����Ȃ��m���́A
�ŁA����Ȃ��m���́A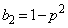 �ł��B
�ł��B�ȉ��A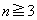 �Ƃ��܂��Bn�̕����̒���
�Ƃ��܂��Bn�̕����̒���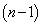 �g����A������2�������A�ǂ��AA�̏��Ԃɕ���ł��Ȃ��Ƃ�(�����Ȃ�m����
�g����A������2�������A�ǂ��AA�̏��Ԃɕ���ł��Ȃ��Ƃ�(�����Ȃ�m����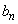 �ł�)�A
�ł�)�A �E1�Ԗڂ�A (�����Ȃ�m����p�ł�)�̂Ƃ��́AA�������Ȃ��̂ŁA2�Ԗڂ͕K��B�ł�(�����Ȃ�m����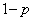 �ł�)�B3�Ԗڂ�A�ł�B�ł��ǂ��̂ł����A3�Ԗڈȍ~��
�ł�)�B3�Ԗڂ�A�ł�B�ł��ǂ��̂ł����A3�Ԗڈȍ~��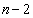 �̕����̒���
�̕����̒���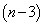 �g����A������2�����́A�ǂ��AA�̏��Ԃɕ���ł��܂���(�����Ȃ�m����
�g����A������2�����́A�ǂ��AA�̏��Ԃɕ���ł��܂���(�����Ȃ�m����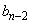 �ł�)�B
�ł�)�B �E1�Ԗڂ�B (�����Ȃ�m����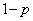 �ł�)�̂Ƃ��́A2�Ԗڂ�A�ł�B�ł��ǂ��̂ł����A2�Ԗڈȏ��
�ł�)�̂Ƃ��́A2�Ԗڂ�A�ł�B�ł��ǂ��̂ł����A2�Ԗڈȏ�� �̕����̒���
�̕����̒���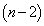 �g����A������2�����́A�ǂ��AA�̏��Ԃɕ���ł��܂���(�����Ȃ�m����
�g����A������2�����́A�ǂ��AA�̏��Ԃɕ���ł��܂���(�����Ȃ�m����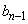 �ł�)�B
�ł�)�B �ȏ���A
����2���������̔��ʎ��ɂ��āA
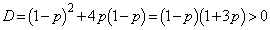 �@(
�@( )
)���A2���������A�͑��قȂ�2�������������܂��B�A�̍��ӂ�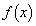 �Ƃ����ƁA
�Ƃ����ƁA ������A2���������A��2��α�Cβ �ɂ��āA
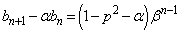 �@����B
�@����B�@ �� 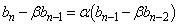
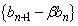 �́A����
�́A����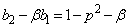 �C����α�̓��䐔��B
�C����α�̓��䐔��B 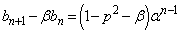 �@����C
�@����C�B�|�C���A
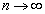 �̂Ƃ��̋Ɍ������߂����̂ł����A
�̂Ƃ��̋Ɍ������߂����̂ł����A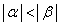 �Ȃ̂ŁA
�Ȃ̂ŁA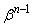 �ł�����܂��B
�ł�����܂��B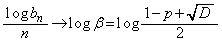
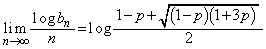 ......[��]
......[��]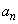 �ɂ��Ă��A
�ɂ��Ă��A �̂Ƃ��A
�̂Ƃ��A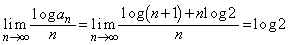
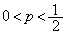 �̂Ƃ��A
�̂Ƃ��A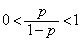 ���A
���A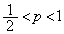 �̂Ƃ��A
�̂Ƃ��A ���A
���A
(3) �E �̂Ƃ��A�A�́A
�̂Ƃ��A�A�́A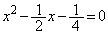
�E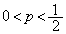 �̂Ƃ��A
�̂Ƃ��A �Ƃ���ƁA
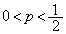 ���s�K�B
���s�K�B�E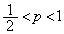 �̂Ƃ��A
�̂Ƃ��A �Ƃ���ƁA
 ���A
���A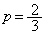
�ȏ���A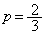 ......[��]���̂Ƃ��A
......[��]���̂Ƃ��A 
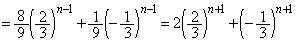 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 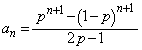
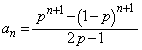 �C
�C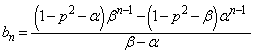

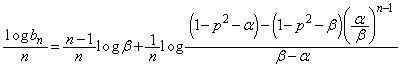
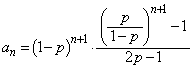
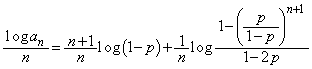
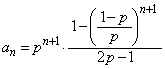

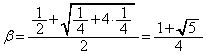
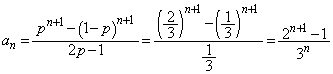 ......[��]
......[��]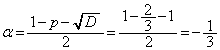 �C
�C