���嗝�n���w'12�N[2]
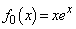 �Ƃ��āA���̐���n�ɑ��āA
�Ƃ��āA���̐���n�ɑ��āA
�ɂ�����x�̊�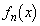 ���߂�B
���߂�B
(1) 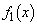 �����߂�B
�����߂�B (2) 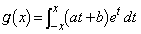 �Ƃ���Ƃ��A��ϕ�
�Ƃ���Ƃ��A��ϕ� �����߂�B�������A����a�Cb�Cc�͒萔�Ƃ���B
�����߂�B�������A����a�Cb�Cc�͒萔�Ƃ���B (3) ���̐���n�ɑ��āA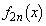 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȑϕ��v�Z��������ꂻ���Ȃ̂ł����A�H�v����A����قǂł��Ȃ��Ȃ�A�Ƃ������ł��B
(1) 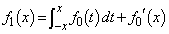

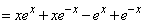 �@����@
�@����@�� 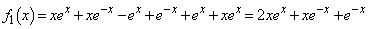 ......[��]
......[��]
(2) 
 �@(�� �A)
�@(�� �A) ......[��]
......[��]�ʉ��D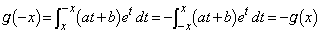 ���A
���A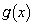 �͊���ł��B
�͊���ł��B ����āA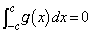
(3) ��蕶���Q������p���čŏ��̕����v�Z���Ă݂܂��B 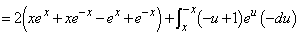 �@(�� �@�C�܂��A
�@(�� �@�C�܂��A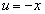 �Ƃ����Ēu���ϕ�)
�Ƃ����Ēu���ϕ�) �@(�� �A)
�@(�� �A)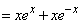
�� 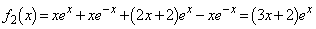
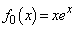 �́A
�́A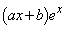 �ŁA
�ŁA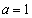 �C
�C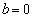 �Ƃ������̂ł��B
�Ƃ������̂ł��B
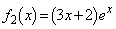 �́A
�́A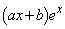 �ŁA
�ŁA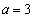 �C
�C �Ƃ������̂ł��B
�Ƃ������̂ł��B
����ŁA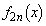 ��1������
��1������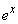 �Ƃ̐ςŕ\����A1�����̒萔����1���̌W����n�Ɉˑ����ĕω�����A�܂�A
�Ƃ̐ςŕ\����A1�����̒萔����1���̌W����n�Ɉˑ����ĕω�����A�܂�A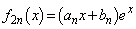 �Ɨ\���ł��܂��B
�Ɨ\���ł��܂��B  �̂Ƃ��A
�̂Ƃ��A ���A
���A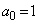 �C
�C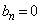 �Ƃ��āA�\���͐��藧���܂��B
�Ƃ��āA�\���͐��藧���܂��B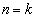 �̂Ƃ��A�\�������藧�Ƃ��āA
�̂Ƃ��A�\�������藧�Ƃ��āA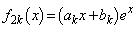 �ƂȂ�܂��B
�ƂȂ�܂��B(2)���A��1���̐ϕ��̓[���ł��B
�� 
������A �C
�C �Ƃ���A
�Ƃ���A ����āA�\����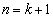 �̂Ƃ������藧���܂��B
�̂Ƃ������藧���܂��B  �ŗ��ӂ������āA
�ŗ��ӂ������āA���� �́A����
�́A����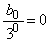 �C����
�C���� �����������ŁA
�����������ŁA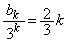
��  �B���A
�B���A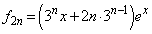 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B