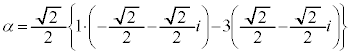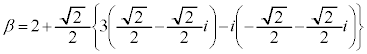��嗝�n���w'24�N�O��[2]
α�Cβ�f���Ƃ��A���f��z�ɑ���
�Ƃ����Bα�Cβ�́A
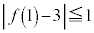 �@���@
�@���@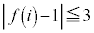
(1) 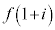 ���Ƃ肤��l�͈̔͂����߁A���f�����ʏ�ɐ}������B
���Ƃ肤��l�͈̔͂����߁A���f�����ʏ�ɐ}������B (2) 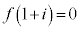 �ł���Ƃ��Aα�Cβ�̒l�����߂�B
�ł���Ƃ��Aα�Cβ�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���嗝�n��24�N[2]�ɂ����Ă��܂����A�V�X���ŕ��j�̗����ɂ������ł��B���嗝�n�Ɠ������O�p�s�����̗��p���\�ł����A�����ł́A(2)�����܂��Aα�Cβ�ɂ��ĉ����Ă��܂��A�Ƃ����l�����ł���Ă݂܂��B
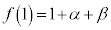 �C
�C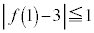 ���(��Βl���Q��)�A
���(��Βl���Q��)�A
������A���f���������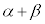 �́A2�𒆐S�Ƃ����a1�̉~�̎���y�ѓ����̓_�ł�(���f�����ʂ̐}�`�I���p���Q��)�B�@����@
�́A2�𒆐S�Ƃ����a1�̉~�̎���y�ѓ����̓_�ł�(���f�����ʂ̐}�`�I���p���Q��)�B�@����@
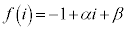 �C
�C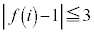 ���A
���A
������A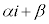 �́A2�𒆐S�Ƃ����a3�̉~�̎���y�ѓ����̓_�ł��B�@����A
�́A2�𒆐S�Ƃ����a3�̉~�̎���y�ѓ����̓_�ł��B�@����A
�@�C�A���ǂ��������ł����A�Ȍ��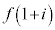 ���ǂ��Ȃ��Ă��邩���l���邽�߂ɂ́A�@�C�A����α�Cβ�����߁A
���ǂ��Ȃ��Ă��邩���l���邽�߂ɂ́A�@�C�A����α�Cβ�����߁A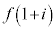 �ɑ������Ƃ�������ɂȂ肻���ł��B�����ŁA�@�ł́A2�𒆐S�Ƃ����a1�̉~�̎���y�ѓ����̓_��\���̂ɁAr��
�ɑ������Ƃ�������ɂȂ肻���ł��B�����ŁA�@�ł́A2�𒆐S�Ƃ����a1�̉~�̎���y�ѓ����̓_��\���̂ɁAr��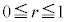 �ł�������Aθ�������Ƃ��A�Ɍ`����p���āA
�ł�������Aθ�������Ƃ��A�Ɍ`����p���āA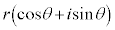 �ƕ\�������Ȃ�̂ł����A����Ŏ��ό`�����Ă����ƁA
�ƕ\�������Ȃ�̂ł����A����Ŏ��ό`�����Ă����ƁA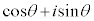 �Ƃ����`���₽��Əo�Ă��Ėʓ|�ł��B�����ŁA
�Ƃ����`���₽��Əo�Ă��Ėʓ|�ł��B�����ŁA
�Ƃ������Ƃɂ��܂��B
���A
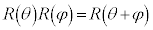 �@����B
�@����B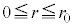 �Ƃ��āA
�Ƃ��āA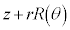 �́A���Sz�C���a
�́A���Sz�C���a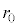 �̉~�̎���y�ѓ����̓_��\���܂�(���f�����ʂ̐}�`�I���p���Q��)�B
�̉~�̎���y�ѓ����̓_��\���܂�(���f�����ʂ̐}�`�I���p���Q��)�B
���D�{��ł́A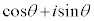 �C
�C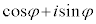 �̌`�̂܂܌v�Z�����s����Ǝ�ɕ����Ȃ��Ȃ�܂��B(2)�����܂��A�ȉ��̂悤�ɁA�B�𗘗p���āA�������̌`
�̌`�̂܂܌v�Z�����s����Ǝ�ɕ����Ȃ��Ȃ�܂��B(2)�����܂��A�ȉ��̂悤�ɁA�B�𗘗p���āA�������̌`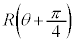 �C
�C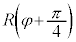 �ɂ��Đ������邱�Ƃ��|�C���g�ł��B
�ɂ��Đ������邱�Ƃ��|�C���g�ł��B
�ȏ���A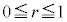 �Ƃ��āA�@�́A
�Ƃ��āA�@�́A
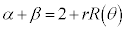 �@����C
�@����C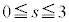 �Ƃ��āA�A�́A
�Ƃ��āA�A�́A
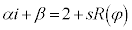 �@����D
�@����D
�C�|�D���A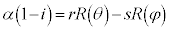
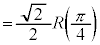 �@����E
�@����E
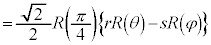
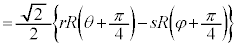 �@����F
�@����F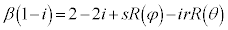
�E���A�B�𗘗p���āA
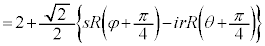 �@����G
�@����G
(1) 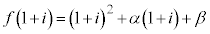
����ɁA�F�C�G�������A
�����ŁA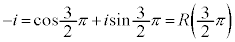 ���A
���A 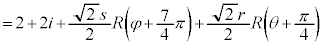 �@����H
�@����H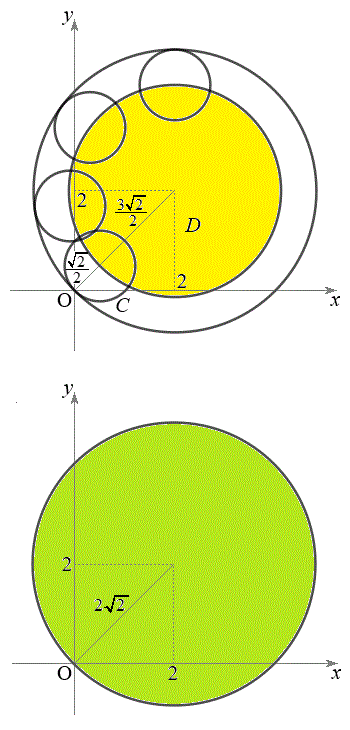 ��L�̂����A
��L�̂����A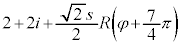 �́A
�́A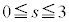 ���A���f�����ʏ�ŁA���S
���A���f�����ʏ�ŁA���S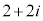 �C���a
�C���a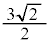 �̉~�̎���y�ѓ���(�̈�D�Ƃ��܂��B�E��}���F���F��)�̓_��\���܂��B
�̉~�̎���y�ѓ���(�̈�D�Ƃ��܂��B�E��}���F���F��)�̓_��\���܂��B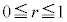 ���A
���A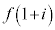 �́A�̈�D���̓_�𒆐S�Ƃ��A���a
�́A�̈�D���̓_�𒆐S�Ƃ��A���a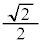 �̉~C�̎���y�ѓ���(�~�ɂ��ẮA�E��}�Q��)�̓_��\���܂��B
�̉~C�̎���y�ѓ���(�~�ɂ��ẮA�E��}�Q��)�̓_��\���܂��B
�~C���A���̒��S���̈�D���ɂ���悤�ɓ������čl����ƁA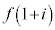 �̂Ƃ肤��l�͈̔͂́A���f�����ʏ�ŁA
�̂Ƃ肤��l�͈̔͂́A���f�����ʏ�ŁA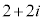 �𒆐S�Ƃ��A���a
�𒆐S�Ƃ��A���a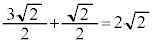 �̉~�̎���y�ѓ����̓_�ɂȂ�܂��B�}������ƉE���}���ΐF���F��(���E�����܂�)�B
�̉~�̎���y�ѓ����̓_�ɂȂ�܂��B�}������ƉE���}���ΐF���F��(���E�����܂�)�B
(2) (1)�̉E�}������킩��ʂ�A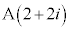 �Ƃ���
�Ƃ���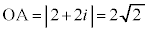 ���AA�𒆐S�Ƃ����a
���AA�𒆐S�Ƃ����a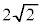 �̉~�͌��_O��ʂ�܂��B���_O�͉~����Ɉʒu���A
�̉~�͌��_O��ʂ�܂��B���_O�͉~����Ɉʒu���A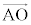 ��x����������̉�]�p��
��x����������̉�]�p��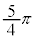 �ł��B����āA�H�ɂ����āA
�ł��B����āA�H�ɂ����āA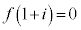 �ƂȂ�̂́Ar�Cs���Ƃ��ɍő��
�ƂȂ�̂́Ar�Cs���Ƃ��ɍő��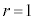 �C
�C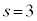 �ł����āA
�ł����āA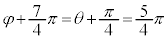 �̂Ƃ��ŁA
�̂Ƃ��ŁA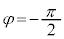 �C
�C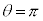 �̂Ƃ��ł��B
�̂Ƃ��ł��B �����ƁA�F�C�G���A
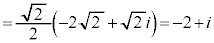 ......[��]
......[��]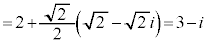 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B