���嗝�n���w'24�N�O��[2]
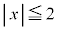 �������f��x�ƁA
�������f��x�ƁA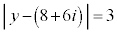 �������f��y�ɑ��āA
�������f��y�ɑ��āA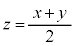 �Ƃ���B���̂悤�ȕ��f��z�����f�����ʂɂ����ē����̈��}�����A���̖ʐς����߂�B
�Ƃ���B���̂悤�ȕ��f��z�����f�����ʂɂ����ē����̈��}�����A���̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������ɂ������Ȃ̂ł����A�ȉ��ł͎O�p�s�����𗘗p���܂��B
α�Cβ�������̂Ƃ��A
���������܂����Aα�Cβ�����f���̂Ƃ��ɂ��A�O�p�s�������������܂��B���f�����ʏ��3�_α�Cβ�C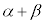 �ɂ��āA0�Cα�Cβ�����̏��Ɉ꒼����ɂ���Ƃ�(
�ɂ��āA0�Cα�Cβ�����̏��Ɉ꒼����ɂ���Ƃ�(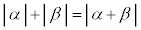 )���܂߁A
)���܂߁A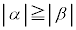 �Ƃ��āA�O�p�`��2�ӂ̘a�͑���1�ӂ��傫��(�O�p�`�̏������Q��)�̂ŁA
�Ƃ��āA�O�p�`��2�ӂ̘a�͑���1�ӂ��傫��(�O�p�`�̏������Q��)�̂ŁA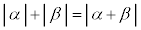 �̏ꍇ���܂߂āA
�̏ꍇ���܂߂āA
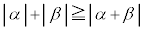 �C
�C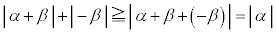
�O�p�s�����F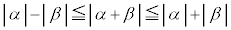 �@���(��)
�@���(��) ���������܂��B�܂��A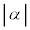 �C
�C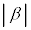 ���Œ肵�Aα��β�̊Ԃ̊p��ω�������ƁA
���Œ肵�Aα��β�̊Ԃ̊p��ω�������ƁA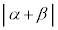 �́A
�́A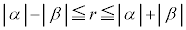 �������ׂĂ̎���r�̒l���Ƃ蓾�܂��B
�������ׂĂ̎���r�̒l���Ƃ蓾�܂��B
���Ay�́A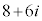 �𒆐S�Ƃ��锼�a3�̉~����̓_�ł�(���f���������Q��)�B
�𒆐S�Ƃ��锼�a3�̉~����̓_�ł�(���f���������Q��)�B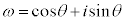 (�Ɍ`�����Q��)�Cθ�͔C�ӂ̎����A�Ƃ��āA
(�Ɍ`�����Q��)�Cθ�͔C�ӂ̎����A�Ƃ��āA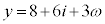 �ƕ\���܂��B
�ƕ\���܂��B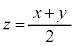 ���A
���A
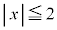 �ɑ������ƁA
�ɑ������ƁA
2�Ŋ���ƁA
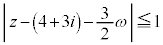 �@����@
�@����@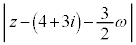 ��0�ȏ�1�ȉ��̂��ׂĂ̎����̒l���Ƃ蓾�܂��B�O�p�s������
��0�ȏ�1�ȉ��̂��ׂĂ̎����̒l���Ƃ蓾�܂��B�O�p�s������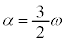 �C
�C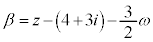 �ƌ���ƁA
�ƌ���ƁA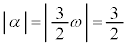 �Ƈ@���
�Ƈ@���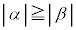 �ł����āA
�ł����āA
�Ƃ���ƁA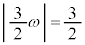 �Ƈ@���A
�Ƈ@���A
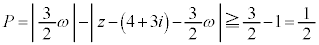 �@����A
�@����A
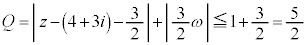 �@����B
�@����B
�A�C�B���A
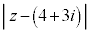 �́A
�́A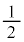 �ȏ�
�ȏ�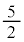 �ȉ��̂��ׂĂ̎����̒l���Ƃ蓾�܂��B
�ȉ��̂��ׂĂ̎����̒l���Ƃ蓾�܂��B
 z�́A
z�́A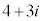 �𒆐S�Ƃ���~����̓_�ł����A���̔��a��
�𒆐S�Ƃ���~����̓_�ł����A���̔��a��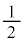 �ȏ�
�ȏ�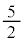 �ȉ��̂��ׂĂ̒l���Ƃ蓾�܂��B
�ȉ��̂��ׂĂ̒l���Ƃ蓾�܂��B
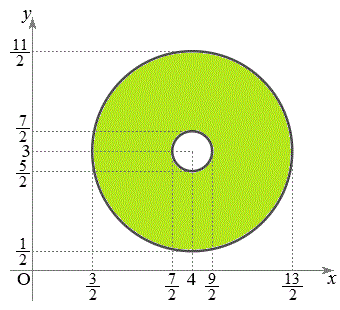
�ȏ���A���f��z�����f�����ʂɂ����ē����̈�́A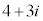 �𒆐S�Ƃ��锼�a
�𒆐S�Ƃ��锼�a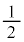 �̉~����O���ł����Ă����a
�̉~����O���ł����Ă����a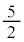 �̉~��������ł��B�}������ƁA�E�}���ΐF���F��(���E�����܂�)�B���̖ʐς́A
�̉~��������ł��B�}������ƁA�E�}���ΐF���F��(���E�����܂�)�B���̖ʐς́A
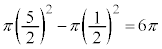 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B