積分法の基礎

積分法の基礎

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

積分法は微分法の逆操作ということができます。ここでは、整関数：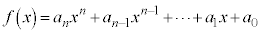

，主として、

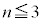の場合について、積分法を扱います。
　定積分の計算により、曲線・直線で囲む面積を計算することができます。

ここで学習する内容は、以下の通りです。各項目をクリックしてください。

不定積分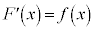　

となるとき、

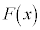から導関数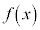

を求める操作を「微分する」と言いますが、

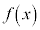から原始関数

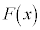を求める操作を「積分する」と言います。

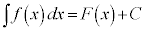(C:：積分定数)と書いて不定積分と言います。
定積分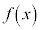　

の原始関数のうちの一つを

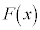だとして、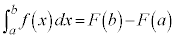

を定積分と言います。不定積分は関数ですが、定積分は値です。
定積分と面積　定積分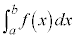

は、曲線

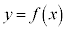の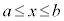

の部分と、x軸の間に挟まれた部分の面積に対応します。
定積分と微分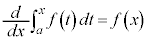　

(積分して微分すると元に戻る)
定積分の公式　定積分の面倒な計算を省力化する公式を学びます。
絶対値を含む定積分　絶対値を含む定積分の計算法を学びます。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。