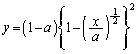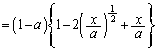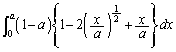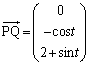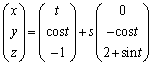慶大理工数学'08年[A1]
(1) 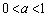 とする。xy平面上で
とする。xy平面上で 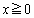 ,
,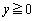 ,
,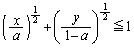
により定められる部分Aの面積は ア である。また空間内でx軸のまわりにAを1回転させてできる回転体の体積は イ である。この体積はa= ウ のときに最大となる。 (2) t を実数とする。空間内の2点P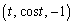 ,Q
,Q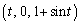 を通る直線とxy平面との交点はR (t, エ ,0)である。t が
を通る直線とxy平面との交点はR (t, エ ,0)である。t が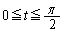 の範囲を動くときに点Rが描く曲線をCとする。xy平面上で、x軸,y軸とCとにより囲まれた部分の面積は オ である。
の範囲を動くときに点Rが描く曲線をCとする。xy平面上で、x軸,y軸とCとにより囲まれた部分の面積は オ である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 素直な微積の計算問題です。(1)も(2)も曲線はx軸と交差しないので、積分区間を分けるというような心配もありません。
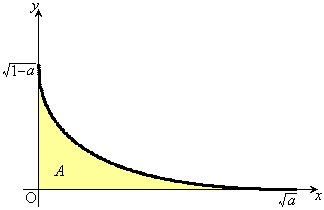
(1)(ア) 部分Aの境界線: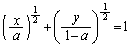 は、
は、
(イ) 回転体の体積Vは、
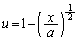 とおく(置換積分を参照)と、
とおく(置換積分を参照)と、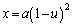 ,
,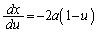 より、
より、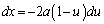 x:
x: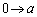 のとき、u:
のとき、u: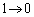
(ウ) 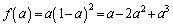 とおくと、
とおくと、 増減表より、Vは、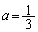 ......[答] のときに最大です。
......[答] のときに最大です。
(2)(エ) 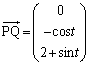
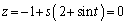 とすると、
とすると、(オ) 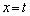 より、
より、 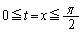 のとき、
のとき、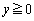 です。
です。
求める面積Sは、ここで、積分計算し易い分母の形にするために、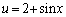 とおきます(置換積分を参照)。
とおきます(置換積分を参照)。
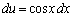 ,x:
,x: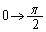 のとき、u:
のとき、u: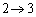
∴ 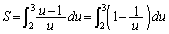
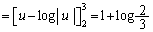 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。