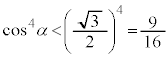���嗝�n���w'22�N�O��[5]
�Ȑ�C�F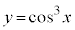 (
(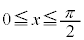 )�Cx�������y���ň͂܂��}�`�̖ʐς�S�Ƃ���B
)�Cx�������y���ň͂܂��}�`�̖ʐς�S�Ƃ���B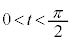 �Ƃ��AC��̓_Q
�Ƃ��AC��̓_Q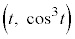 �ƌ��_O�C�����P
�ƌ��_O�C�����P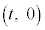 �CR
�CR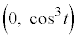 �_�ɂ������`OPQR�̖ʐς�
�_�ɂ������`OPQR�̖ʐς�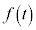 �Ƃ���B���̂Ƃ��A���̊e��ɓ�����B
�Ƃ���B���̂Ƃ��A���̊e��ɓ�����B
(1) S�����߂�B
(2) 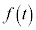 �͍ő�l������1��t �łƂ邱�Ƃ������B���̂Ƃ���t ��α�Ƃ���ƁA
�͍ő�l������1��t �łƂ邱�Ƃ������B���̂Ƃ���t ��α�Ƃ���ƁA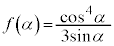 �ł��邱�Ƃ������B
�ł��邱�Ƃ������B (3) 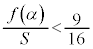 �������B
�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ϕ��̌v�Z���ł��B �Ƃ�
�Ƃ�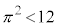 �Ƃ������q���g���Ȃ��̂ŁA(3)�͐��l�I�ɓ����邱�Ƃɂ��܂��B
�Ƃ������q���g���Ȃ��̂ŁA(3)�͐��l�I�ɓ����邱�Ƃɂ��܂��B
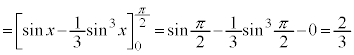 ......[��]
......[��]
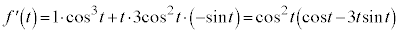 �@(�ς̔����@�A�������̔����@�A�����̌������Q��)
�@(�ς̔����@�A�������̔����@�A�����̌������Q��)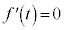 �Ƃ���ƁA
�Ƃ���ƁA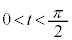 �ɂ����Ă�
�ɂ����Ă�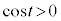 �Ȃ̂ŁA
�Ȃ̂ŁA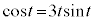 �ƂȂ�܂����At ��0����
�ƂȂ�܂����At ��0����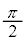 �܂ŕω�����Ƃ��A
�܂ŕω�����Ƃ��A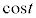 ��1����0�܂ŒP���Ɍ������A
��1����0�܂ŒP���Ɍ������A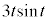 ��0����
��0����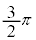 �܂ŒP���ɑ������܂��B�]���āA
�܂ŒP���ɑ������܂��B�]���āA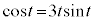 �́A
�́A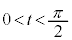 �͈̔͂ɂ���1�̉�α�������܂��Bα�́A
�͈̔͂ɂ���1�̉�α�������܂��Bα�́A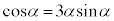 �@����@�@�����܂��B
�@����@�@�����܂��B
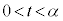 �ɂ����āA
�ɂ����āA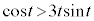 �C
�C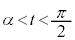 �ɂ����āA
�ɂ����āA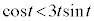
����āA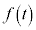 �̑����\�͈ȉ��̂悤�ɂȂ�܂�(���̑������Q��)�B �����\���A
�̑����\�͈ȉ��̂悤�ɂȂ�܂�(���̑������Q��)�B �����\���A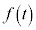 �͍ő�l������1��t �łƂ邱�Ƃ��킩��܂��B����t ��α�ŁA
�͍ő�l������1��t �łƂ邱�Ƃ��킩��܂��B����t ��α�ŁA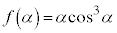 �ł��A
�ł��A
�@���A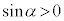 ��
��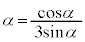 �C����āA
�C����āA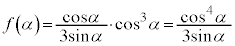 ......[��]
......[��]
(3) �܂��@��p���āAα���ǂꂭ�炢�̐��Ȃ̂��ׂ܂��B
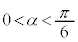 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA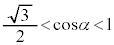 �C
�C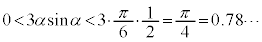
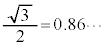 �ƂȂ�A�@���������܂���(�O�p�����Q��)�B
�ƂȂ�A�@���������܂���(�O�p�����Q��)�B
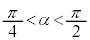 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA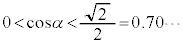 �C
�C
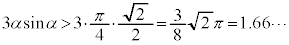 �ƂȂ�A�@���������܂���B
�ƂȂ�A�@���������܂���B
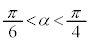 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA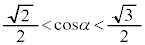 �C�܂�A
�C�܂�A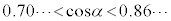
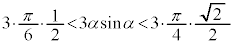 �C�܂�A
�C�܂�A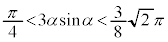 �C
�C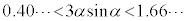 �ƂȂ�A
�ƂȂ�A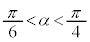 �ɂ����āA
�ɂ����āA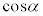 ��α�̌������A
��α�̌������A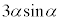 ��α�̑������ŁA�@����������α�����݂��܂��B
��α�̑������ŁA�@����������α�����݂��܂��B
����āA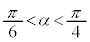 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A
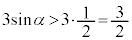 ���A
���A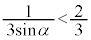
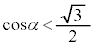 �C
�C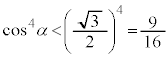 (2)���A
(2)���A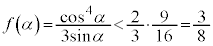
�����(1)���A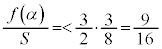
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 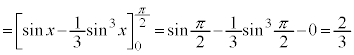 ......[��]
......[��]