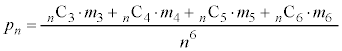京大理系数学'24年前期[1]
n個の異なる色を用意する。立方体の各面にいずれかの色を塗る。各面にどの色を塗るかは同様に確からしいとする。辺を共有するどの二つの面にも異なる色が塗られる確率を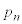
とする。次の問いに答えよ。
(1) 
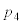を求めよ。 (2) 
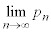を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 うまい考え方を追求すれば、より良い解法があると思いますが、ここでは、試験会場でのことを考え、平凡に実戦的に具体的に考えてみます。
辺を共有するどの二つの面にも異なる色が塗られる、という条件を、条件(＊)とします。
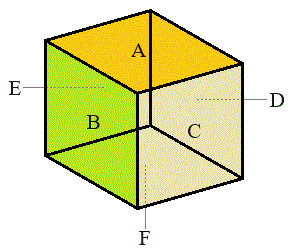(1) 立方体の各面を右図のようにA〜Fと名前を付けます。AとF，BとD，CとEは対向する面で隣り合わない面です。・立方体の各面を、条件(＊)に従い、ちょうど1色，またはちょうど2色で塗り分けることはできません。
・立方体の各面を、条件(＊)に従い、ちょうど3色で塗り分ける方法の数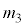
は、 Aの色が3通り、Bの色がAで使った色以外の2通り、Cの色がA，Bで使った色以外の残る1通り、Dの色はBと同じ色、Eの色はCと同じ色、Fの色はAと同じ色、よって(場合の数を参照)、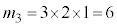 
通り・立方体の各面を、条件(＊)に従い、ちょうど4色で塗り分ける方法の数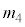
は、 Aの色が4通り、Bの色がAで使った色以外の3通り、Cの色がA，Bで使った色以外の2通り、Dの色はBと同じ色を使うか、残る1色を使うかです。Eの色は、A，B，D以外の色になりますが、
前者の場合(DがBと同じ色)、EはCと同じ色か、残る1色か、で、どちらの場合もFはAと同じ色です。
後者の場合(Dは残る1色)、EはCと同じ色、FはAと同じ色です。
よって、
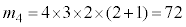通り・立方体の各面を、条件(＊)に従い、ちょうど5色で塗り分ける方法の数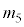
は、 Aの色が5通り、Bの色がAで使った色以外の4通り、Cの色がA，Bで使った色以外の3通り、Dの色はBと同じ色を使うか、残る2色のどちらかを使うかです。Eの色は、A，B，D以外の色になりますが、
前者の場合(DがBと同じ色)、Eは残る2色のどちらかとなり、Fは最後に残った1色になります。
後者の場合(Dは残る2色のどちらか)、EはCと同じ色を使う(このときFは残る1色)か、残る1色(Fは、B，C，D，Eのいずれとも異なるのでAと同じ色)かです。
よって、
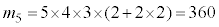通り・立方体の各面を、条件(＊)に従い、ちょうど6色で塗り分ける方法の数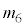
は、 
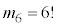通り立方体の各面に4色のいずれかを塗る方法の数は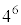
通り(重複順列を参照)あり、その各1通りは同様に確からしい。
立方体の各面を、条件(＊)に従い、4色で塗り分ける方法は、3色で塗り分ける場合、4色から3色を選んで塗り分ける方法の数が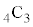
通りあり、 
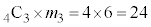通りちょうど4色で塗り分けるのが、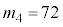
通り
よって(確率を参照)、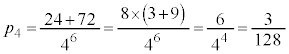
......[答]
(2) 立方体の各面にn色のいずれかを塗る方法の数は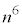
通りあり、その各1通りは同様に確からしい。 立方体の各面をちょうど7色以上全て使って塗り分けることはないので、n色(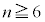
)のいずれかで塗り分けるとき、(1)より、実際に使われる色は、3色，4色，5色，6色のいずれかです。n色から実際に塗り分けに使われる3色，4色，5色，6色を選ぶ方法の数は、
，
，
，
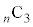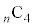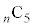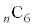通り(組み合わせを参照)なので、 よって、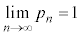
......[答]使える色の数を増やすと、条件(＊)を満たすように必ず塗り分けられるようになっていく、ということです。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
，
(