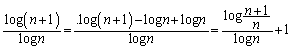���H�吔�w'02�N�O��[4]
n�����R���Ƃ���B
(1) ���̋Ɍ������߂�B
(2) ��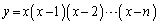 �̋ɒl��^����x�̍ŏ��l��
�̋ɒl��^����x�̍ŏ��l��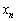 �Ƃ���B���̂Ƃ�
�Ƃ���B���̂Ƃ� �����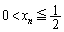 �������B
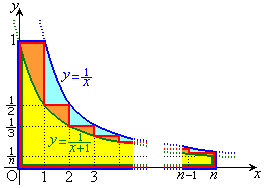
�������B (3) (2)��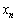 �ɑ��āA�Ɍ�
�ɑ��āA�Ɍ� �����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
 ���@(1)�̇A�����K�i�^���̋Z�I��p���āA�E�}�ŁA
���@(1)�̇A�����K�i�^���̋Z�I��p���āA�E�}�ŁA
�ΐ���������̖ʐρ��Ԑ���������̖ʐρ�����������̖ʐ�
���l����A�����ɓ����܂��B
(2)�́An���������ɂ��ẮA�����������A�w���@�ɂ��Ă��ؖ��̋Z�I���Q�Ƃ��Ă��������B
(1) 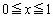 �ɂ����āA
�ɂ����āA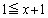 ���A
���A �� 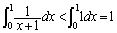 ����@
����@
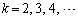 �̂Ƃ��A
�̂Ƃ��A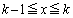 �ɂ����āA
�ɂ����āA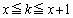 ���A
���A �� 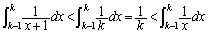 �e�ӂ�
�e�ӂ�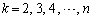 �ɂ��ĉ������킹�āA
�ɂ��ĉ������킹�āA �@���A���ӂ�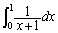 �������A���ӂƉE�ӂ�1�������Ă��s�����͐��藧���܂��B
�������A���ӂƉE�ӂ�1�������Ă��s�����͐��藧���܂��B
�� 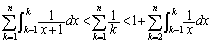 �@����A�@(��ϕ��Ɩʐ����Q��)
�@����A�@(��ϕ��Ɩʐ����Q��) ���A
�e�ӂ�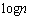 �Ŋ����āA
�Ŋ����āA 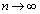 �̂Ƃ��A
�̂Ƃ��A�� 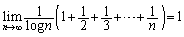 ......[��]
......[��]
(2) 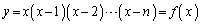 ��
��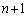 �����ł��B
�����ł��B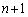 ���������F
���������F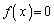 �́A
�́A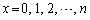 �����ɂ����܂��B
�����ɂ����܂��B �܂��A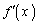 ��n�����ŁA
��n�����ŁA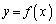 �̃O���t���l����ƁA
�̃O���t���l����ƁA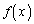 �́A
�́A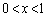 �C
�C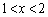 �C����C
�C����C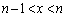 �̊e�͈͂ɋɒl��1�����̂ŁAn���������F
�̊e�͈͂ɋɒl��1�����̂ŁAn���������F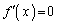 �́A
�́A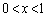 �C
�C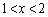 �C����C
�C����C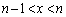 �̊e�͈͂ɉ���1���A�S����n�����܂��B����ȊO�ɂ́A
�̊e�͈͂ɉ���1���A�S����n�����܂��B����ȊO�ɂ́A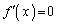 �̉��͂���܂���B
�̉��͂���܂���B
�Ƃ������Ƃ́A��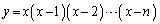 �̋ɒl��^����x�̍ŏ��l
�̋ɒl��^����x�̍ŏ��l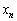 �́A
�́A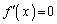 ��
��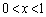 �ɂ�������ł����āA
�ɂ�������ł����āA
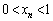 �@����F
�@����F
�����藧���܂��B
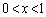 �̂Ƃ��A
�̂Ƃ��A �F���A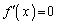 �́A
�́A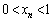 �ł���悤�ȉ�
�ł���悤�ȉ�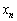 �������Ă��āA
�������Ă��āA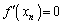 �C
�C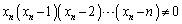 ���A
���A �� 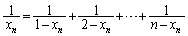 ����G
����G
�����ŁA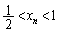 �Ɖ��肷��ƁA�G�̍��ӂɂ��āA
�Ɖ��肷��ƁA�G�̍��ӂɂ��āA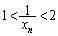 �ł����A�G�̉E�ӂɂ��āA
�ł����A�G�̉E�ӂɂ��āA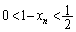 �C
�C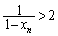 �ł���A
�ł���A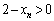 �C����C
�C����C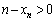 �ł�����A�G�̉E�ӂ��A
�ł�����A�G�̉E�ӂ��A �ƂȂ�A�����G�����������Ȃ��Ȃ�܂��B�Ƃ������Ƃ́A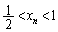 �Ƃ�������͌��ł��B�F�ƍ��킹�āA
�Ƃ�������͌��ł��B�F�ƍ��킹�āA
�� 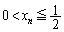 ����H
����H
(3) �H���A
����āA
�]���āA�ӁX�������킹��ƁA
�E�ӂɂ��ẮA
�� 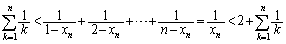 �e�ӂ�
�e�ӂ�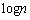 �Ŋ���ƁA
�Ŋ���ƁA ������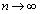 �Ƃ���ƁA(1)���A
�Ƃ���ƁA(1)���A
���H��́A�͂��݂����̌��������܂��g�����ƂŋɌ������߂��肪�����̂ł����A������ƌ���Ǝ�̂��ɂ����Ɍ��̖����A���ȒP�ȋɌ��ɒu�������čl���Ă䂭�A�Ƃ����̂��e�[�}�ɂȂ��Ă��܂��B������̂܂܌�������Ȃ��ŁA�������₷���`�ɒ����čl���悤�Ƃ������z������܂��B�{����Y��ȍ\�z�𗧂Ă�悤�ɂȂ��Ă��܂����A�K�X�q���g�ɏ���Ă��܂�������A�u���Ȋ�����������ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B