���H�吔�w'06�N�O��[2]
�ȉ��̖�ɓ�����B
(1) a�Cb�𐳂̒萔�Ƃ��A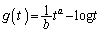 �Ƃ����B
�Ƃ����B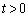 �ɂ������
�ɂ������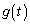 �̑����ɒl�����߂�B
�̑����ɒl�����߂�B (2) m�𐳂̒萔�Ƃ��Axy���W���ʂɂ����ď���
�����_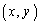 ����Ȃ�̈��D�Ƃ���BD�̊T�`��}������B
����Ȃ�̈��D�Ƃ���BD�̊T�`��}������B (3) (2)�̗̈�D�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�W���I�Ȕ��ϕ��̌v�Z���ł��B�v�Z�~�X�ɂ悭���ӂ��Ă��������B
�����\���A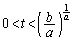 �ɂ����Č����A
�ɂ����Č����A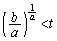 �ɂ����đ����ŁA
�ɂ����đ����ŁA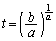 �ɂ����ċɏ��l�F
�ɂ����ċɏ��l�F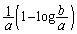 ......[��]�@(���̑������Q��)
......[��]�@(���̑������Q��)
(2) (b)�̏�������A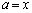 �C
�C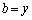 �Ƃ���(1)�𗘗p����ƁA
�Ƃ���(1)�𗘗p����ƁA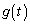 �̍ŏ��l
�̍ŏ��l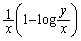 ��m�ȏ�ł���悢�̂ŁA(a)�̏������A���ӂ�x�������Đ�������ƁA
��m�ȏ�ł���悢�̂ŁA(a)�̏������A���ӂ�x�������Đ�������ƁA �� 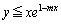 �@����@(a)�̏������������邽�߂ɁA
�@����@(a)�̏������������邽�߂ɁA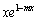 ��x�̑召�W�ׂ܂��B
��x�̑召�W�ׂ܂��B ����́A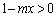 �C�܂�A
�C�܂�A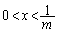 �̂Ƃ��ɕ��A
�̂Ƃ��ɕ��A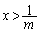 �̂Ƃ��ɐ��ŁA
�̂Ƃ��ɐ��ŁA
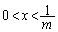 �̂Ƃ���
�̂Ƃ���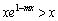 �C
�C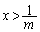 �̂Ƃ���
�̂Ƃ���
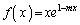 �Ƃ��āA�Ȑ�
�Ƃ��āA�Ȑ�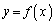 �ׂ܂��B
�ׂ܂��B 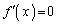 �Ƃ���ƁA
�Ƃ���ƁA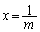 �C
�C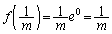
�T�`��}�����邾���Ȃ̂ŁA�ʏ�͑����ׂ�Ώ\���ł����A�����ł́A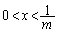 �ɂ�����Ȑ��̋������m�F���邽�߂ɁA���ʂ����ׂ邱�Ƃɂ��܂�(���̉������Q��)�B
�ɂ�����Ȑ��̋������m�F���邽�߂ɁA���ʂ����ׂ邱�Ƃɂ��܂�(���̉������Q��)�B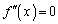 �Ƃ���ƁA
�Ƃ���ƁA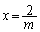 �C
�C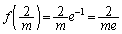
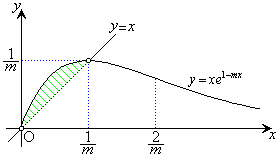 �����\���A�Ȑ�
�����\���A�Ȑ�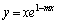 �ƒ���
�ƒ���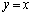 �́A
�́A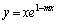 ���ɑ�ƂȂ�_
���ɑ�ƂȂ�_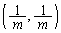 �Ō���邱�Ƃ��킩��܂��B
�Ō���邱�Ƃ��킩��܂��B
�ȏ���A���߂�̈�D�́A�E�}�ΐ���(�Ȑ�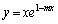 ���
���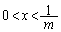 �̕������܂݁A����
�̕������܂݁A����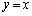 �������)
�������)
(3) ����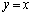 �ƒ���
�ƒ���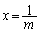 �Cx���ň͂܂��O�p�`�̖ʐς́A
�Cx���ň͂܂��O�p�`�̖ʐς́A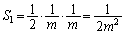
�Ȑ�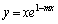 �ƒ���
�ƒ���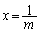 �Cx���ň͂܂��̈�̖ʐ�(��ϕ��Ɩʐ����Q��)�́A
�Cx���ň͂܂��̈�̖ʐ�(��ϕ��Ɩʐ����Q��)�́A ���߂�ʐς́A
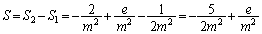 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B