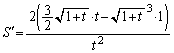���H�吔�w'09�N���[2]
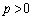 �C
�C �ł���悤�ȓ_P
�ł���悤�ȓ_P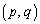 ����o�Ȑ�
����o�Ȑ� �ֈ�����2�{�̐ڐ��̐ړ_��A�CB�Ƃ���B
�ֈ�����2�{�̐ڐ��̐ړ_��A�CB�Ƃ���B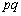 ��t�Ƃ����āA�O�p�`PAB�̖ʐς�t�̎��Ƃ��ĕ\���B�܂��A���̖ʐς̍ŏ��l�����߂�B
��t�Ƃ����āA�O�p�`PAB�̖ʐς�t�̎��Ƃ��ĕ\���B�܂��A���̖ʐς̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������Ԃ��l����ƁA�Â炸�ɕ��}�Ɍv�Z��i�߂�����ǂ������ł��B
�_A�CB��x���W��a�Cb ( )�Ƃ��܂��B
)�Ƃ��܂��B
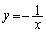 �C
�C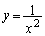
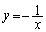 ��
��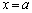 �ɂ������ڐ��́A
�ɂ������ڐ��́A
�_P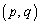 ��ʂ�̂ŁA
��ʂ�̂ŁA
�������a�ɂ��Đ�������ƁA
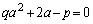 �@����@
�@����@
�ƂȂ�̂ŁA�@�͑��قȂ�2������a�Cb�������܂��B���ƌW���̊W���A
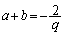 �C
�C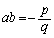 �@����A
�@����A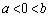 �ł��BA�CB�̍��W��
�ł��BA�CB�̍��W��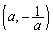 �C
�C
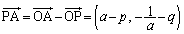 �C
�C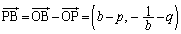
�����ŁA2���������@��2���̍�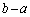 �́A
�́A
����ƇA��p���āA
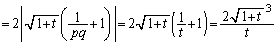 ......[��]�@(
......[��]�@(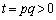 �ł�)
�ł�) �ɂ�����
�ɂ�����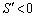 �C
�C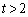 �ɂ�����
�ɂ����� ���AS�́A
���AS�́A �̂Ƃ��ɍŏ��l
�̂Ƃ��ɍŏ��l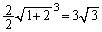 ......[��]�@(���̑������Q��)
......[��]�@(���̑������Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B