���H�吔�w'12�N�O��[5]
�s��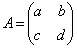 �Œ�܂�1���ϊ���f �Ƃ���B���_O
�Œ�܂�1���ϊ���f �Ƃ���B���_O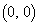 �ƈقȂ�C�ӂ�2�_P�CQ�ɑ���
�ƈقȂ�C�ӂ�2�_P�CQ�ɑ���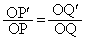 �����藧�B�������A
�����藧�B�������A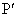 �C
�C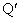 �͂��ꂼ��P�CQ��f �ɂ�鑜��\���B
�͂��ꂼ��P�CQ��f �ɂ�鑜��\���B
(1) 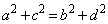 �������B
�������B (2) 1���ϊ�f �ɂ��A�_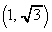 ���_
���_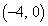 �Ɉڂ�Ƃ��AA�����߂�B
�Ɉڂ�Ƃ��AA�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����ϊ�(1���ϊ�(����2)���Q��)���ނƂ�����ŁA�c�嗝�H'09�N[B1]�ɂ��ޑ肪�o�肳��Ă��܂��B
��蕶��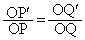 �Ƃ����̂́A���_�ȊO�̔C�ӂ̓_P�ɂ��āA
�Ƃ����̂́A���_�ȊO�̔C�ӂ̓_P�ɂ��āA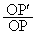 ����肾�Ƃ������Ƃł��B
����肾�Ƃ������Ƃł��B
(1) 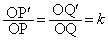 �@����@
�@����@ 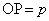 (
(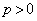 )�COP��x���Ƃ��Ȃ��p��θ �Ƃ���ƁAP�̍��W��
)�COP��x���Ƃ��Ȃ��p��θ �Ƃ���ƁAP�̍��W��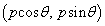 �ƕ\���܂��B
�ƕ\���܂��B���A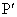 �̍��W�́A
�̍��W�́A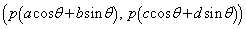
�@���A�C�ӂ̊pθ �ɂ��āA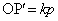
���ꂪ�A�C�ӂ̊pθ �ɂ��Đ������邽�߂ɁA
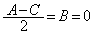 �C
�C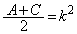 �@����A
�@����A�Ȃ��Ȃ�A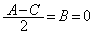 �łȂ���A
�łȂ���A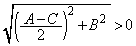 ���A
���A ���A���l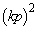 �ƂȂ邱�Ƃ͂���܂���B
�ƂȂ邱�Ƃ͂���܂���B
�A���A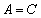 �A�����A
�A�����A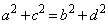 �@����B
�@����B
�܂��A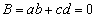 �@����C�@�����藧���܂��B
�@����C�@�����藧���܂��B
(2) �B���A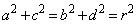 (
(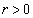 )�Ƃ��āA
)�Ƃ��āA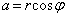 �C
�C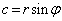 �Ƃ������Ƃ��ł��܂��B�C���AA
�Ƃ������Ƃ��ł��܂��B�C���AA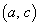 �CB
�CB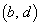 �Ƃ��āA
�Ƃ��āA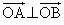 �ł�(�������Q��)�B
�ł�(�������Q��)�B ������A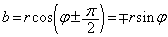 �C
�C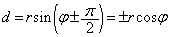 (��������)�ƂȂ�܂��B����āA
(��������)�ƂȂ�܂��B����āA 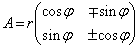 �@(��������)�@����D
�@(��������)�@����D
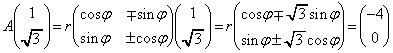
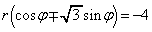 �@����E�C
�@����E�C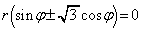 �@����F
�@����F�F���A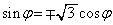
�E�ɑ������ƁA 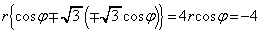 �@(��������)
�@(��������)�� 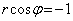 �F���A
�F���A �@��
�@�� 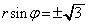
�D�ɑ�����āA 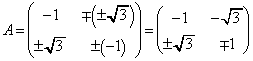 �@(��������) ......[��]
�@(��������) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 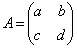 �Œ�܂�
�Œ�܂�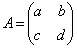 �Œ�܂�1���ϊ���f �Ƃ���B���_O
�Œ�܂�1���ϊ���f �Ƃ���B���_O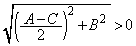 ���A
���A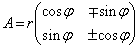 �@(��������)�@����D
�@(��������)�@����D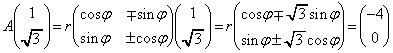
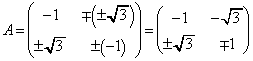 �@(��������) ......[��]
�@(��������) ......[��]