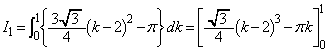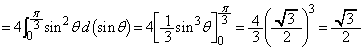���H�吔�w'12�N�O��[6]
xyz��Ԃ�4�_P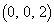 �CA
�CA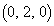 �CB
�CB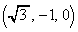 �CC
�CC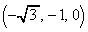 ���Ƃ�B�l�ʑ�PABC��
���Ƃ�B�l�ʑ�PABC��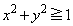 ���݂��������̑̐ς����߂�B
���݂��������̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f�ʐς�ϕ����邾�����̐��̖��ł����A�Ȃ��Ȃ��X���i���Ƃ͂����܂���B���嗝�n05�N�O��[6]�C���嗝�n98�N�O��[6]�Ǝ��Ă��܂����A�{��̕����������ۂ��܂��B
�l�ʑ�PABC��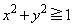 ���݂���������T�Ƃ��܂��B
���݂���������T�Ƃ��܂��B
����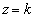 �Ő����Ƃ��̒f�ʂ��l���܂��B
�Ő����Ƃ��̒f�ʂ��l���܂��B
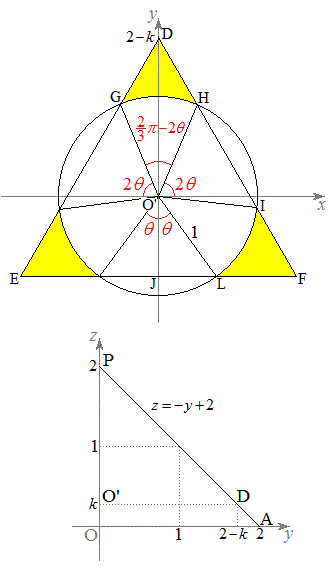
�l�ʑ̂�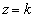 �Ő�ƁA�f�ʂ͉E��}�̐��O�p�`DEF�ƂȂ�A�}�`T�̒f�ʂ͉��F���F���ƂȂ�܂��B���̖ʐ�
�Ő�ƁA�f�ʂ͉E��}�̐��O�p�`DEF�ƂȂ�A�}�`T�̒f�ʂ͉��F���F���ƂȂ�܂��B���̖ʐ�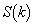 �́A�Ώ̐����l���Az���ƕ���
�́A�Ώ̐����l���Az���ƕ���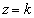 �Ƃ̌�_��
�Ƃ̌�_��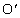 �Ƃ��āA���O�p�`DEF�̖ʐς���A��`
�Ƃ��āA���O�p�`DEF�̖ʐς���A��`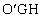 �̖ʐςƎO�p�`
�̖ʐςƎO�p�`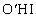 �̖ʐς̘a��3�{�����������̂ɂȂ�܂��B
�̖ʐς̘a��3�{�����������̂ɂȂ�܂��B
�E���}�ŁA����PA�̕������́A
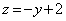 �@����@
�@����@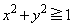 �̋��E����
�̋��E����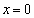 �Ƃ���
�Ƃ���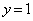 �ƂȂ�̂ŁA�}�`T�����݂���z�͈̔͂̏�[�͇@��
�ƂȂ�̂ŁA�}�`T�����݂���z�͈̔͂̏�[�͇@��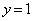 �Ƃ��āA
�Ƃ��āA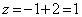 �C����āA�}�`T�́A
�C����āA�}�`T�́A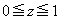 �̕����ɑ��݂��܂��B
�̕����ɑ��݂��܂��B
D��y���W�͇@��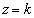 �Ƃ��āA
�Ƃ��āA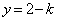
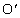 ����EF�ɉ��낵�������̑���J�Ƃ���ƁA
����EF�ɉ��낵�������̑���J�Ƃ���ƁA
���O�p�`DEF�̖ʐ�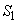 �́A
�́A
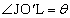 �Ƃ����(θ �̂Ƃ���́A���k�̐ϕ���θ �̐ϕ��ɒu���ϕ����邱�Ƃ��l�����đI�Ԃ悤�ɂ��܂��B�{��ł́A�������d�v�ȃ|�C���g�ł�)�A�O�p�`
�Ƃ����(θ �̂Ƃ���́A���k�̐ϕ���θ �̐ϕ��ɒu���ϕ����邱�Ƃ��l�����đI�Ԃ悤�ɂ��܂��B�{��ł́A�������d�v�ȃ|�C���g�ł�)�A�O�p�`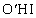 �̖ʐ�
�̖ʐ�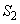 �́A
�́A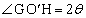 ���A
���A
��`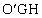 �̖ʐ�
�̖ʐ�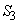 �́A
�́A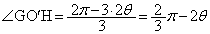 ���A
���A
θ ��k�Ƃ̊W�́A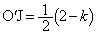 ���A
���A
�� 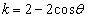 �@����A
�@����A
�}�`T�̑̐�V�́A
��1���̐ϕ��́A
��2���A��3���̐ϕ��́A�A�ɂ�����u���ϕ����邱�Ƃɂ��A
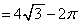 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B