���H�吔�w'22�N�O��[2]
3�̐��̐���a�Cb�Cc�̍ő����1�ł���Ƃ��A���̖₢�ɓ�����B
(1) 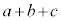 �C
�C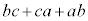 �C
�C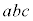 �̍ő����1�ł��邱�Ƃ������B
�̍ő����1�ł��邱�Ƃ������B (2) 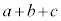 �C
�C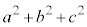 �C
�C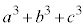 �̍ő���ƂȂ�悤�Ȑ��̐��������ׂċ��߂�B
�̍ő���ƂȂ�悤�Ȑ��̐��������ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�́A�u�ő������1�v�ƍl����Ɠ���̂ŁA�ے���l���A�u�ő����1�łȂ��v�A�܂�A�u2�ȏ�̍ő�������v�Ɖ��肷��ƌ��ɂȂ邱�Ƃ��A�w���@�ŏؖ����܂��B(2)�͓��ł��B�����ł͒��ׂ�Ώۂ����肵����ŃV���~�ׂ��ł���Ă݂܂��B
(1) 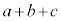 �C
�C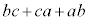 �C
�C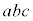 ��2�ȏ�̌���m�����Ɖ��肵�܂��Bd�Ce�Cf�����R���Ƃ��āA
��2�ȏ�̌���m�����Ɖ��肵�܂��Bd�Ce�Cf�����R���Ƃ��āA 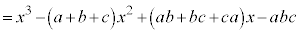
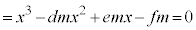 �@����@
�@����@�̉��ł��B
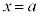 �͇@�̉��Ȃ̂ŁA
�͇@�̉��Ȃ̂ŁA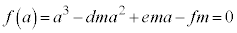
����āA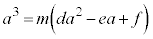
�܂�Aa��m�̔{���ł��B
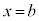 �͇@�̉��Ȃ̂ŁA
�͇@�̉��Ȃ̂ŁA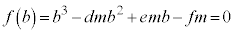
����āA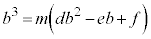
�܂�Ab��m�̔{���ł��B
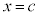 �͇@�̉��Ȃ̂ŁA
�͇@�̉��Ȃ̂ŁA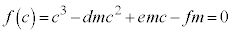
����āA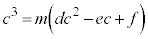
�܂�Ac��m�̔{���ł��B
����āAa�Cb�Cc��2�ȏ�̌���m�������ƂɂȂ�A�ő����1�Ƃ��������Ɩ������܂��B����āA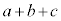 �C
�C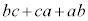 �C
�C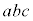 ��2�ȏ�̌���m�����Ƃ�������͌��ł��B�����A
��2�ȏ�̌���m�����Ƃ�������͌��ł��B�����A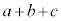 �C
�C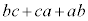 �C
�C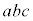 �̍ő����1�ł��B
�̍ő����1�ł��B
(2) 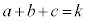 �C
�C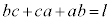 �C
�C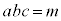 �C
�C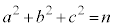 �C
�C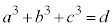 �Ƃ����ƁA(1)���Ak�Cl�Cm�̍ő����1�ł��B
�Ƃ����ƁA(1)���Ak�Cl�Cm�̍ő����1�ł��B �����ŁAk�Cn�Cd������j�����Ƃ���ƁAp�Cq�Cr�����R���Ƃ��āA
�Ƃ����܂��B
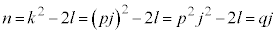 �@��
�@�� 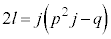 �@����B
�@����B
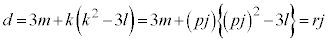 �@����C
�@����C
�� 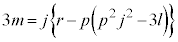 �@����D
�@����Dj��5�����傫���f��(�܂�Ak�Cn�Cd��5�ȏ�̑f��j�����Ɏ���)���Ƃ���ƁAj��2�C3�ƌ݂��ɑf�Ȃ̂ŁA�A�C�B�C�D���Ak�Cl�Cm��j�̔{���ƂȂ�(1)�ɔ����܂��B����āAk�Cn�Cd��5�ȏ�̑f�������Ɏ����܂���B
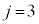 �̂Ƃ��A�A�C�B�C�D���A
�̂Ƃ��A�A�C�B�C�D���A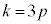 �C
�C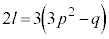 �C
�C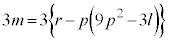 �@����E
�@����E
������Al��3�̔{���ł��Br��s�����R���Ƃ��āA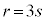 �Ƃ�����Ƃ��A�E���A
�Ƃ�����Ƃ��A�E���A �ƂȂ�m��3�̔{���ł��B���̂Ƃ��Ak�Cl�Cm��3�̔{���ƂȂ�(1)�ɔ����܂��B
�����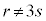 �ł��B���̂Ƃ��A�A���A
�ł��B���̂Ƃ��A�A���A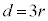 ��3�̔{���ł����A9�̔{���ł͂���܂���B�܂�Ak�Cn�Cd�̍ő����9�ɂȂ邱�Ƃ͂���܂���B
��3�̔{���ł����A9�̔{���ł͂���܂���B�܂�Ak�Cn�Cd�̍ő����9�ɂȂ邱�Ƃ͂���܂���B
�����ŁA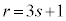 �Ƃ�����(��]�����Q��)�Ƃ��A�E���A
�Ƃ�����(��]�����Q��)�Ƃ��A�E���A ���A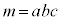 ��3�Ŋ����1�]�鐔�ł��B
��3�Ŋ����1�]�鐔�ł��B
�Ⴆ�A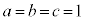 �̂Ƃ��A
�̂Ƃ��A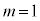 �ƂȂ�m��3�Ŋ����1�]��܂����A���̂Ƃ��A
�ƂȂ�m��3�Ŋ����1�]��܂����A���̂Ƃ��A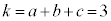 �C
�C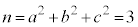 �C
�C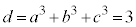 �́A�ő����3�ł��B
�́A�ő����3�ł��B
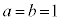 �C
�C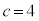 �̂Ƃ��A
�̂Ƃ��A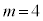 �ƂȂ�m��3�Ŋ����1�]��܂����A���̂Ƃ��A
�ƂȂ�m��3�Ŋ����1�]��܂����A���̂Ƃ��A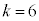 �C
�C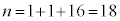 �C
�C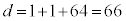 �̍ő����6�ł��B
�̍ő����6�ł��B ���D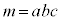 ��3�Ŋ�����1�]�鐔�ɂȂ�̂́Aa�Cb�Cc�����ꂼ��3�Ŋ������]��̑g�ݍ��킹���A
��3�Ŋ�����1�]�鐔�ɂȂ�̂́Aa�Cb�Cc�����ꂼ��3�Ŋ������]��̑g�ݍ��킹���A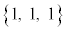 �C
�C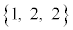 �ƂȂ�ꍇ�ł��B
�ƂȂ�ꍇ�ł��B �܂��A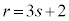 �Ƃ�����Ƃ��A�E���A
�Ƃ�����Ƃ��A�E���A 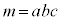 ��3�Ŋ����2�]�鐔�ł����Aa�Cb�Cc���������3�Ŋ�����2�]�鐔�̂Ƃ��A
��3�Ŋ����2�]�鐔�ł����Aa�Cb�Cc���������3�Ŋ�����2�]�鐔�̂Ƃ��A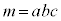 ��3�Ŋ����2�]��܂��B���̂Ƃ��A
��3�Ŋ����2�]��܂��B���̂Ƃ��A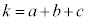 ��3�̔{���ł��B�Ⴆ�A
��3�̔{���ł��B�Ⴆ�A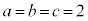 �̂Ƃ��A
�̂Ƃ��A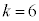 �C
�C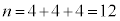 �C
�C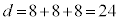 �̍ő����6�ł��B
�̍ő����6�ł��B���D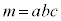 ��3�Ŋ�����2�]�鐔�ɂȂ�̂́Aa�Cb�Cc�����ꂼ��3�Ŋ������]��̑g�ݍ��킹���A
��3�Ŋ�����2�]�鐔�ɂȂ�̂́Aa�Cb�Cc�����ꂼ��3�Ŋ������]��̑g�ݍ��킹���A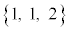 �C
�C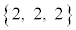 �ƂȂ�ꍇ�ł��B
�ƂȂ�ꍇ�ł��B 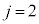 �̂Ƃ��A�A�C�B�C�D���A
�̂Ƃ��A�A�C�B�C�D���A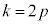 �C
�C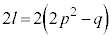 �C
�C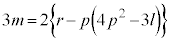 �@����F
�@����F
������Ak�Cm�͋����ł����A����q���������Ƃ����l�������ŁAk�Cl�Cm������2�������ƂɂȂ�(1)�ɔ����܂��B�����q�͊�ł����A���̂Ƃ��A�A�ŁA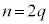 �͋����ł���4�̔{���ɂ͂Ȃ�܂���B�܂�Ak�Cn�Cd�̍ő����4�ɂȂ邱�Ƃ͂���܂���B
�͋����ł���4�̔{���ɂ͂Ȃ�܂���B�܂�Ak�Cn�Cd�̍ő����4�ɂȂ邱�Ƃ͂���܂���B
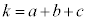 �C
�C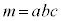 �������ŁA
�������ŁA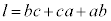 ����ƂȂ�̂́Aa�Cb�Cc�̂����ꂩ1�����������A������̏ꍇ�ł��B�Ⴆ�A
����ƂȂ�̂́Aa�Cb�Cc�̂����ꂩ1�����������A������̏ꍇ�ł��B�Ⴆ�A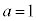 �C
�C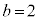 �C
�C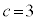 �̏ꍇ�A
�̏ꍇ�A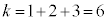 �C
�C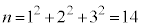 �C
�C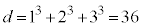 �̍ő����2�ł��B
�̍ő����2�ł��B
�ȏ���A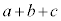 �C
�C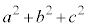 �C
�C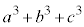 �́A5�ȏ�̑f�������Ɏ����Ƃ͂Ȃ��A2�C3�����Ɏ����Ƃ͂����Ă��A
�́A5�ȏ�̑f�������Ɏ����Ƃ͂Ȃ��A2�C3�����Ɏ����Ƃ͂����Ă��A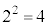 �C
�C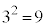 �����Ɏ����Ƃ͂Ȃ��A�ő���ƂȂ�\���̂��鐳�̐����́A1�C2�C3�C6�Ɍ����܂��B����5�ȏ�̑f���ɂȂ邱�Ƃ͂Ȃ��̂ŁAa�Cb�Cc��1��5(
�����Ɏ����Ƃ͂Ȃ��A�ő���ƂȂ�\���̂��鐳�̐����́A1�C2�C3�C6�Ɍ����܂��B����5�ȏ�̑f���ɂȂ邱�Ƃ͂Ȃ��̂ŁAa�Cb�Cc��1��5(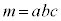 ��5�̔{��)�C�Ⴆ�A
��5�̔{��)�C�Ⴆ�A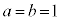 �C
�C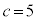 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA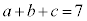 �C
�C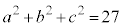 �C
�C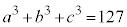 �̍ő����1�ɂȂ�܂�(���ɂ��A
�̍ő����1�ɂȂ�܂�(���ɂ��A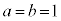 �C
�C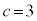 �̂Ƃ��A
�̂Ƃ��A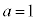 �C
�C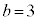 �C
�C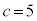 �̂Ƃ��A�Ȃ�)�B
�̂Ƃ��A�Ȃ�)�B
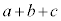 �C
�C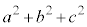 �C
�C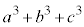 �̍ő���ƂȂ�悤�Ȑ��̐����́A
�̍ő���ƂȂ�悤�Ȑ��̐����́A1 (�Ⴆ��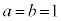 �C
�C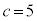 �̂Ƃ�)�C2 (�Ⴆ��
�̂Ƃ�)�C2 (�Ⴆ��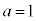 �C
�C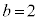 �C
�C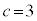 �̂Ƃ�)�C3 (�Ⴆ��
�̂Ƃ�)�C3 (�Ⴆ��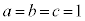 �̂Ƃ�)�C6 (�Ⴆ��
�̂Ƃ�)�C6 (�Ⴆ��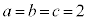 �̂Ƃ�) ......[��]
�̂Ƃ�) ......[��] ���D���̗v���́A�ő���ƂȂ鐳�̐��������߂邱�ƂŁA�ő����1�C2�C3�C6�ȊO�ɂ͂Ȃ�Ȃ����Ƃ������A�ő����1�C2�C3�C6�ɂȂ����e�X1������悭�A�ǂ������ꍇ�ɍő����1�C2�C3�C6�ɂȂ邩�A�Ƃ������Ƃł͂Ȃ��̂Œ��ӂ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B