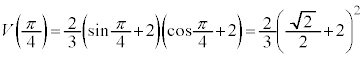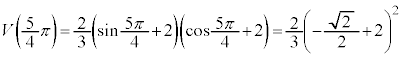ÈwåHwnw'25NOú[2]
óÔÌ_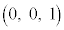 ðÊè
ðÊè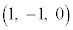 ðûüxNgÆ·é¼üð
ðûüxNgÆ·é¼üð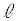 ƵA_
ƵA_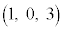 ðÊè
ðÊè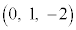 ðûüxNgÆ·é¼üðmÆ·éB
ðûüxNgÆ·é¼üðmÆ·éB
(1) Pð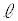 ãÌ_ƵAQðmãÌ_Æ·éBܽA¼üPQͼü
ãÌ_ƵAQðmãÌ_Æ·éBܽA¼üPQͼü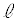 ƼümɼŠéÆ·éB±ÌÆ«PÆQÌÀWA¨æÑüªPQÌ·³ðßæB
ƼümɼŠéÆ·éB±ÌÆ«PÆQÌÀWA¨æÑüªPQÌ·³ðßæB (2) 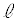 ãÉ2_
ãÉ2_ ª èAmãÉ2_
ª éÆ·éB½¾µAt ÍÀÆ·éBlÊÌABCDÌÌÏð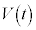 Æ·éB
Æ·éB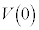 ðßæB
ðßæB (3) t ª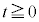 ð®Æ«A
ð®Æ«A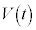 ÌÅålÆŬlðßæB
ÌÅålÆŬlðßæB
@
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@{âÅÍAâè¶ð©Ä·®ÉCñƪ èÜ·B¼ü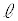 ÌûüxNgÌz¬ªª0Å
ÌûüxNgÌz¬ªª0Å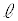 ãÌ2_ACBÌzÀWªÆàÉ1Å é±ÆÆA¼ümÌûüxNgÌz¬ªª0ÅmãÌ2_CCDÌxÀWªÆàÉ1Å é±ÆÅ·B±êÍA{âÌdåÈqgÅȺÅͱêðpµÄl¦Ä¢±ÆɵܷBȨAóÔxNgðQƵľ³¢B
ãÌ2_ACBÌzÀWªÆàÉ1Å é±ÆÆA¼ümÌûüxNgÌz¬ªª0ÅmãÌ2_CCDÌxÀWªÆàÉ1Å é±ÆÅ·B±êÍA{âÌdåÈqgÅȺÅͱêðpµÄl¦Ä¢±ÆɵܷBȨAóÔxNgðQƵľ³¢B
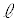 ÌûüxNgÌz¬ªÍ0Å èA¼ü
ÌûüxNgÌz¬ªÍ0Å èA¼ü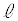 Í_
Í_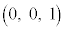 ðÊéÌÅA¼ü
ðÊéÌÅA¼ü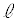 ͽÊ
ͽÊ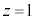 ã̼üÅ·BÀÛÉ
ã̼üÅ·BÀÛÉ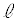 ãÌ2_ACBÌzÀWÍ1Å·B@¥¥¥@
ãÌ2_ACBÌzÀWÍ1Å·B@¥¥¥@
mÌûüxNgÌx¬ªÍ0Å èA¼ümÍ_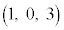 ðÊéÌÅA¼ümͽÊ
ðÊéÌÅA¼ümͽÊ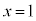 ã̼üÅ·BÀÛÉmãÌ2_CCDÌxÀWÍ1Å·B@¥¥¥A
ã̼üÅ·BÀÛÉmãÌ2_CCDÌxÀWÍ1Å·B@¥¥¥A
@æèA¼ü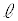 ãÌ_
ãÌ_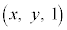 ÍAtðÀƵÄA
ÍAtðÀƵÄA
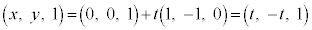 @¥¥¥B
@¥¥¥B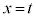 C
C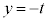 æèA
æèA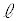 ãÌ_É¢Ä
ãÌ_É¢Ä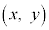 ÍA
ÍA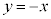 ð½µÜ·B
ð½µÜ·B
AæèA¼ümãÌ_ ÍAsðÀƵÄA
ÍAsðÀƵÄA
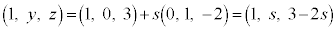 @¥¥¥C
@¥¥¥C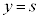 C
C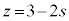 æèAmãÌ_É¢Ä
æèAmãÌ_É¢Ä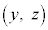 ÍA
ÍA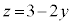 @¥¥¥D
@¥¥¥D
ð½µÜ·B
(1) BCCæè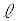 ãÌ_P
ãÌ_P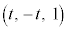 CmãÌ_Q
CmãÌ_Q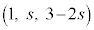 É¢ÄA
É¢ÄA 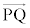 ÍA
ÍA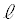 ÌûüxNg
ÌûüxNg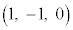 ƼÅA
ƼÅA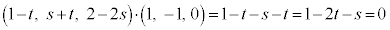 @¥¥¥E
@¥¥¥E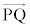 ÍAmÌûüxNg
ÍAmÌûüxNg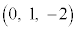 ƼÅA
ƼÅA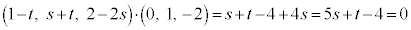 @¥¥¥F
@¥¥¥FEæè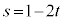 CFÉãüµÄA
CFÉãüµÄA 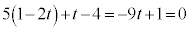 @
@ 
EÉãüµÄA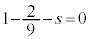 @
@ 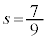 æÁÄAPÌÀWÍ
æÁÄAPÌÀWÍ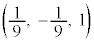 ......[]CQÌÀWÍ
......[]CQÌÀWÍ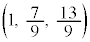 ......[]
......[]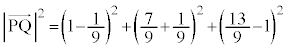
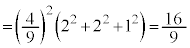 @
@ 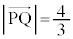 ......[]
......[]
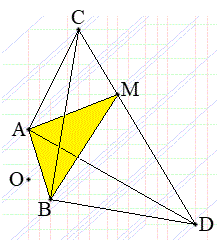 (2)
(2) 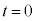 ÌÆ«AA
ÌÆ«AA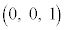 CB
CB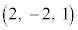 CC
CC CD
CD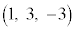 Å èA@æèüªCDƽÊ
Å èA@æèüªCDƽÊ ÆÌÖWð²×éÆACÌzÀWÍ1æèå«ADÌzÀWÍ1æ謳AE}Ìæ¤ÉüªCDͽÊ
ÆÌÖWð²×éÆACÌzÀWÍ1æèå«ADÌzÀWÍ1æ謳AE}Ìæ¤ÉüªCDͽÊ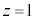 Æð_Mð¿ADÅ
Æð_Mð¿ADÅ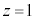 Æ·éÆA
Æ·éÆA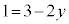 æè
æè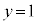 ÅAMÌÀWÍ
ÅAMÌÀWÍ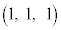 @¥¥¥G
@¥¥¥G±ÌÆ«AlÊÌABCDð½Ê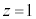 ÅØéÆAlÊÌCABMÆlÊÌDABMɪ©êÜ·B2ÂÌlÊÌÌêÊÅ é¢ABM(½Ê
ÅØéÆAlÊÌCABMÆlÊÌDABMɪ©êÜ·B2ÂÌlÊÌÌêÊÅ é¢ABM(½Ê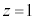 ãÉ é)ÌÊÏSÍA
ãÉ é)ÌÊÏSÍA CÌzÀWÍ3C¢ABMͽÊ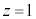 ãÉ éÌÅAlÊÌCABM̳Í2CDÌzÀWÍ
ãÉ éÌÅAlÊÌCABM̳Í2CDÌzÀWÍ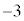 ÈÌÅAlÊÌDABM̳Í4Å·BæÁÄAlÊÌABCDÌÌÏ
ÈÌÅAlÊÌDABM̳Í4Å·BæÁÄAlÊÌABCDÌÌÏ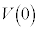 ÍAHæèA
ÍAHæèA 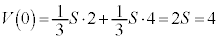 ......[]
......[]
(3) 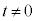 ÌÆ«ÉàA(2)Ư¶æ¤ÉvZµ½¢ÌÅ·ªA
ÌÆ«ÉàA(2)Ư¶æ¤ÉvZµ½¢ÌÅ·ªA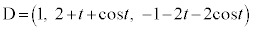 ÌzÀWÍA
ÌzÀWÍA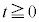 ÌÆ«A
ÌÆ«A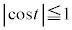 æè
æè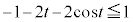 ÈÌÅADͽÊ
ÈÌÅADͽÊ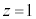 ©çº¤É èÜ·ªA
©çº¤É èÜ·ªA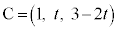 ÌzÀWÍA
ÌzÀWÍA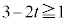 CÂÜèA
CÂÜèA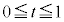 ÌÆ«ÉÍACͽÊ
ÌÆ«ÉÍACͽÊ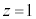 ©çãÉA
©çãÉA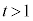 ÌÆ«ÉÍACͽÊ
ÌÆ«ÉÍACͽÊ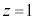 æèàºÉ èÜ·B
æèàºÉ èÜ·B CÆDÌzÀWÉ¢ÄA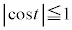 æè
æè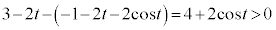 ÈÌÅA
ÈÌÅA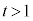 ÌêÅàA¼ümãÅA3_MCCCDÍã©ç±ÌÉÀÑÜ·B@¥¥¥I
ÌêÅàA¼ümãÅA3_MCCCDÍã©ç±ÌÉÀÑÜ·B@¥¥¥I
ȨAMª¼ümƽÊ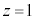 ÆÌð_Åà é±ÆÉÓ·éÆA
ÆÌð_Åà é±ÆÉÓ·éÆA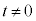 ÌÆ«ÉàAMÌÀWÍ
ÌÆ«ÉàAMÌÀWÍ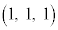 Å·B
Å·B E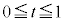 ÌÆ«AlÊÌABCDð½Ê
ÌÆ«AlÊÌABCDð½Ê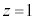 ÅØéÆAÌϪ0ÉÈéêàÜßÄAlÊÌCABMÆlÊÌDABMɪ©êÜ·B2ÂÌlÊÌÌêÊÅ é¢ABMÌÊÏSÍA
ÅØéÆAÌϪ0ÉÈéêàÜßÄAlÊÌCABMÆlÊÌDABMɪ©êÜ·B2ÂÌlÊÌÌêÊÅ é¢ABMÌÊÏSÍA 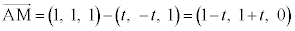 C
C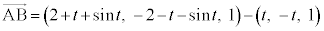
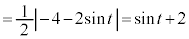 @(
@(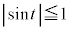 æè³Å·)@¥¥¥J
æè³Å·)@¥¥¥JCÌzÀWÍ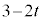 ÈÌÅAlÊÌCABM̳Í
ÈÌÅAlÊÌCABM̳Í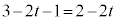 ClÊÌDABM̳Í
ClÊÌDABM̳Í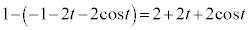 Å·BlÊÌABCDÌÌÏ
Å·BlÊÌABCDÌÌÏ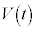 ÍAJæèA
ÍAJæèA 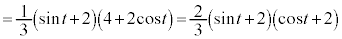 @¥¥¥K
@¥¥¥KE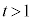 ÌÆ«AlÊÌCABM̳Í
ÌÆ«AlÊÌCABM̳Í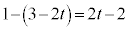 ClÊÌDABM̳Í
ClÊÌDABM̳Í ÌÜÜÅ·BlÊÌABCDÌÌÏÍAIæèAlÊÌDABMÌÌÏ©çlÊÌCABMÌÌÏðø¢½àÌÉÈèAlÊÌABCDÌÌÏ
ÌÜÜÅ·BlÊÌABCDÌÌÏÍAIæèAlÊÌDABMÌÌÏ©çlÊÌCABMÌÌÏðø¢½àÌÉÈèAlÊÌABCDÌÌÏ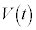 ÍAJæèA
ÍAJæèA 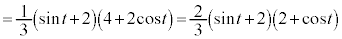 @¥¥¥L
@¥¥¥LæÁÄKCLæèA¢¸êÌêà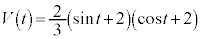 Å·B
Å·B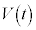 Íüú
Íüú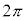 ÌüúÖÈÌÅA
ÌüúÖÈÌÅA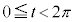 ÌÍÍÅl¦Ü·B
ÌÍÍÅl¦Ü·B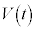 ð÷ª·éÆA
ð÷ª·éÆA ±±ÅA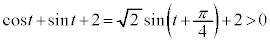 (
(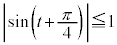 )æèA
)æèA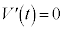 ÌÆ«
ÌÆ«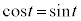 C¦¿A
C¦¿A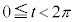 ÌÍÍÅÍA
ÌÍÍÅÍA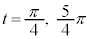 (2)ÌÊæè
(2)ÌÊæè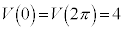
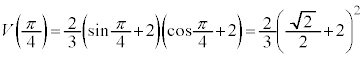
æèA¸\ÍȺÌæ¤ÉÈèÜ·B
¸\æèA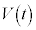 ÌÅålÍ
ÌÅålÍ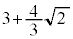 C
C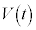 ÌŬlÍ
ÌŬlÍ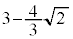 ......[]
......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@ÈwåwTOP@@wTOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B