ÈwåHwnw'25NOú[3]
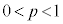 Æ·éB\ªoém¦ªpC ªoém¦ª
Æ·éB\ªoém¦ªpC ªoém¦ª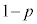 Å é1ÌRCðgÁÄÌQ[ðs¤B
Å é1ÌRCðgÁÄÌQ[ðs¤B
EQ[ÌJniKÅ_Í0_B
ERC𰱯A\ªoé²ÆÉ1_ÁZµA ªo½Æ«Í_Í»ÌÜÜB
E2ñ±¯Ä ªo½çQ[ÍI¹B
0ÈãÌ®nÉεAQ[ªIíÁ½Æ«Én_ÆÈÁÄ¢ém¦ð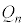 Æ·éB
Æ·éB
(1) 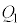 C
C ðpðp¢Ä\¹B
ðpðp¢Ä\¹B (2) 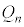 ðnÆpðp¢Ä\¹B
ðnÆpðp¢Ä\¹B (3)  ð½·ÀxÉεĮª¬è§Â±Æð¦¹B
ð½·ÀxÉεĮª¬è§Â±Æð¦¹B KvÈçÎA ÌÆ«
ÌÆ«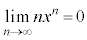 Å é±ÆðؾȵÅgÁÄàæ¢B
Å é±ÆðؾȵÅgÁÄàæ¢B (4) ³À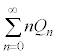 ðpðp¢Ä\¹B
ðpðp¢Ä\¹B
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@âè¶ÉuQ[ªIíÁ½Æ«vÆ©êÄ¢éÌÅAÅãÉ2ñ±¯Ä ªo½êðl¦é±ÆÉÈèÜ·B3ñ±¯Ä ªoé±ÆÍÈ¢ÌÅA\ðZA ðÆ\·ÆAÅãÌ3ñÍZÉÈèÜ·BÅãÌ3ñÉ¢ÄZÆÈém¦Í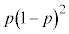 Å·B@¥¥¥@
Å·B@¥¥¥@
(1) Q[ªIíÁ½Æ«1_ÆÈÁÄ¢éÌÍAÅãÌ3ñªZÅA±ÌÉZª1ñ éÌÅA±ÌÈOÉZÍ èܹñBª3ñA±·é±ÆÍÈ¢ÌÅAÅãÌ3ñÈOÍAܾnßĢȢ©AÌ¢¸ê©Å·B@æèAOÒÌêÌm¦Í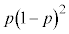 CãÒÌêÌm¦Í
CãÒÌêÌm¦Í Å èA¼ÒÍr½ÈÌÅAßém¦
Å èA¼ÒÍr½ÈÌÅAßém¦ ÍA
ÍA 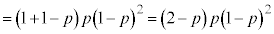 ......[]
......[]Q[ªIíÁ½Æ«2_ÆÈÁÄ¢éÌÍAÅãÌ3ñÌÉZª1ñ éÌÅA±ÌÈOÉZª1ñ èÜ·Bª2ñ±Æ»±ÅI¹µÄµÜ¤ÌÅAÅãÌ3ñÈOÉ¢ı¤ÈéoûÍA(i) ZC(ii) ZC(iii) ZC(iv) ZÌ¢¸ê©Å·B@æèA
(i)Ìm¦ÍA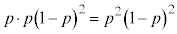
(ii)Ìm¦ÍA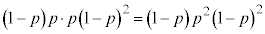
(iii)Ìm¦ÍA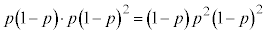
(iv)Ìm¦ÍA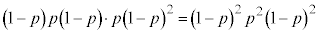
(i)C(ii)C(iii)C(iv)Ír½ÅAßém¦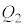 ÍA
ÍA 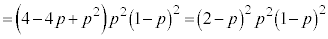 ......[]
......[]
(2) (1)ƯlÉl¦Ü·BQ[ªIíÁ½Æ«Én_ÆÈÁÄ¢éÌÍAÅãÌ3ñÌÈ©ÉZª1ñ éÌÅA±ÌÈOÉZª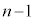 ñ èÜ·Bª2ñ±Æ»±ÅI¹µÄµÜ¤ÌÅA±¤ÈéoûÍA
ñ èÜ·Bª2ñ±Æ»±ÅI¹µÄµÜ¤ÌÅA±¤ÈéoûÍA ñÌZðÀ×ÄÅ«é
ñÌZðÀ×ÄÅ«é ÂÌZÌÀÑÌOãAZÆZÌÔAí¹ÄnÂÌÊuɪüé©üçÈ¢©ª èAȺÅÍÌÊuª
ÂÌZÌÀÑÌOãAZÆZÌÔAí¹ÄnÂÌÊuɪüé©üçÈ¢©ª èAȺÅÍÌÊuª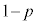 ÉÈé±ÆÉÓµÄA
ÉÈé±ÆÉÓµÄA ¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
¥¥¥¥¥¥
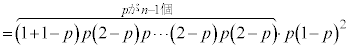 @(pÌÀÑÌÔAOãÌnJÉ
@(pÌÀÑÌÔAOãÌnJÉ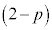 ªüèÜ·)
ªüèÜ·) @¥¥¥A
@¥¥¥AQ[ªIíÁ½Æ«0_ÉÈéÌÍÆoéêÅA»Ìm¦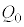 Í
Í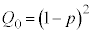 Å·BAÍ
Å·BAÍ ÌÊðÜÝÜ·BæÁÄA
ÌÊðÜÝÜ·BæÁÄA  ......[]
......[]ÊðDÈãÌ®Ï`ÍA³XÌ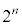 ÂÌÌaðAE¤©ç2¸ÂÌaðÜÆßÄ¢é(ÜÆßé½ÑÉ
ÂÌÌaðAE¤©ç2¸ÂÌaðÜÆßÄ¢é(ÜÆßé½ÑÉ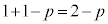 ª1¸ÂoÄé)ÌÅ·ªAª©èÉ¢©àmêܹñBQ»®ð§ÄÄðµÄÝÜ·B
ª1¸ÂoÄé)ÌÅ·ªAª©èÉ¢©àmêܹñBQ»®ð§ÄÄðµÄÝÜ·B 1ñÚÉZªoÄQ[ªI¹µ½Æ«Én_ÆÈém¦ð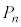 C1ñÚɪoÄQ[ªI¹µ½Æ«Én_ÆÈém¦ð
C1ñÚɪoÄQ[ªI¹µ½Æ«Én_ÆÈém¦ð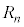 ƵܷB¼ÒÍr½Å
ƵܷB¼ÒÍr½Å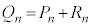 Å·B
Å·B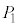 Í@æèA
Í@æèA Å·B
Å·B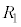 Í(1)ÌZÌêÅA
Í(1)ÌZÌêÅA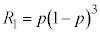 Å·B1ñÚÉZªoÄQ[ªI¹µ½Æ«É
Å·B1ñÚÉZªoÄQ[ªI¹µ½Æ«É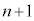 _ÆÈém¦
_ÆÈém¦ ÍA2ñÚÉZªoÄ2ñÚÈ~̾_ªn_ÉÈéê(m¦
ÍA2ñÚÉZªoÄ2ñÚÈ~̾_ªn_ÉÈéê(m¦ )ÆA2ñÚÉC3ñÚÉZªoÄ3ñÚÈ~̾_ªn_ÉÈéê(m¦
)ÆA2ñÚÉC3ñÚÉZªoÄ3ñÚÈ~̾_ªn_ÉÈéê(m¦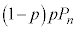 )ðí¹ÄA
)ðí¹ÄA 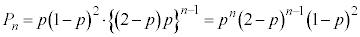 @¥¥¥B
@¥¥¥B1ñÚɪoÄQ[ªI¹µ½Æ«É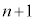 _ÆÈém¦
_ÆÈém¦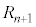 ÍA2ñÚÉZªoÄ3ñÚÈ~Ån_ÆÈéêÅABðp¢ÄA
ÍA2ñÚÉZªoÄ3ñÚÈ~Ån_ÆÈéêÅABðp¢ÄA  ƨÆA
ƨÆA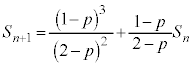 @¥¥¥C
@¥¥¥C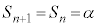 ƨÆA
ƨÆA @¥¥¥D
@¥¥¥D@ @
@ 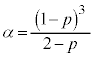 C|DæèA
C|DæèA ±êæèA ÍA
ÍA Cöä
Cöä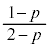 ÌäñÅA
ÌäñÅA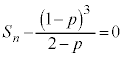
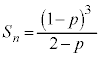 C
C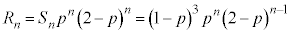
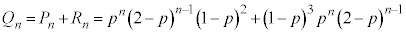
ÆÈèÜ·B
(3) 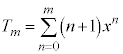 ƨÆA
ƨÆA Å·B
Å·B ±êæèA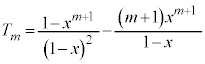
±±Å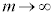 Æ·éÆA
Æ·éÆA Å·BܽA
Å·BܽA ÌÆ«
ÌÆ«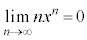 ÈÌÅA
ÈÌÅA Å·BæÁÄA
Å·BæÁÄA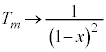 Å èA
Å èA ª¬è§¿Ü·B
ª¬è§¿Ü·B D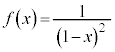 ðmñ÷ª·éÆA
ðmñ÷ª·éÆA
(4) AæèA
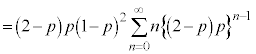
 @(nð1¸絽)
@(nð1¸絽)(3)ÌÊÅ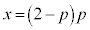 Æ©éÆA
Æ©éÆA  ......[]
......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@ÈwåwTOP@@wTOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 
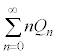 ðpðp¢Ä\¹B
ðpðp¢Ä\¹B
 ƨÆA
ƨÆA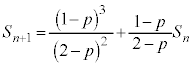 @¥¥¥C
@¥¥¥C @¥¥¥D
@¥¥¥D @
@ 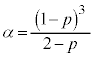
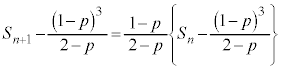
 ÍA
ÍA Cöä
Cöä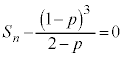
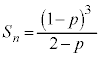 C
C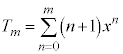 ƨÆA
ƨÆA Å·B
Å·B
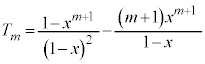
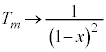 Å èA
Å èA ª¬è§¿Ü·B
ª¬è§¿Ü·B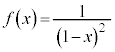 ðmñ÷ª·éÆA
ðmñ÷ª·éÆA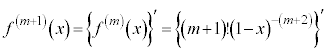
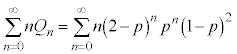
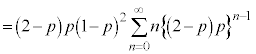
 @(nð1¸絽)
@(nð1¸絽)
 ......[]
......[]